manim边做边学--显函数图像

TOOP精选

于 2025-06-04 05:40:33 发布

阅读量32

点赞数

合集 - manim(92)

91. manim边做边学--显函数图像 06-01

92.manim边做边学--隐函数图像06-02

在Manim库中，FunctionGraph类是一个核心组件，专门用于在坐标系中绘制函数图像。

FunctionGraph的主要作用是将数学函数以直观的图形形式展示出来，使得复杂的数学概念更加容易理解。它广泛应用于数学教学、科学演示以及数据可视化等领域。

其典型应用场景包括：

数学教学：直观展示函数的基本形状和性质（奇偶性、周期性、渐近线等）
物理模拟：可视化运动学中的位移-时间图像、速度-时间图像
工程应用：绘制信号处理中的波形图、控制系统中的响应曲线
算法演示：展示优化算法中的目标函数、机器学习中的损失函数

本文将详细介绍FunctionGraph的功能、参数和应用场景，并通过实际示例展示其强大功能。

1. 主要参数

FunctionGraph的主要参数有：

参数	类型	说明
`function`	Callable[[float], float]	必需参数，要绘制的函数（如`lambda x: x**2`）
`x_range`	Sequence[float]	定义域，如`[-3, 3]` 或`[-3, 3, 0.1]` （起点、终点、步长）
`color`	Color	曲线颜色，默认为`WHITE`
`discontinuities`	Sequence[float]	函数的不连续点列表
`use_smoothing`	bool	是否使用平滑处理（默认`True`）
`dt`	float	参数化步长（影响平滑度）
`t_range`	Optional[Sequence[float]]	参数范围（高级用法）

其中，function是核心参数，表示要绘制的函数。

它是一个可调用的函数对象，通常是一个lambda表达式或定义好的函数。

2. 主要方法

FunctionGraph的主要方法有：

名称	说明
`get_function`	返回用于绘制图像的函数对象。这在需要获取或修改函数时非常有用
`get_point_from_function`	根据给定的参数值，返回函数图像上的对应点。这在需要获取特定点的坐标时非常方便

3. 使用示例

下面通过几个示例来演示如何使用FunctionGraph来绘制函数图像。

3.1. 正弦和余弦函数图像

这个示例展示了如何绘制正弦和余弦函数的图像。通过指定不同的颜色，可以清晰地区分两个函数。

# 绘制正弦函数图像
sin_func = FunctionGraph(
    lambda t: np.sin(t),
    color=BLUE,
)
# 绘制余弦函数图像
cos_func = FunctionGraph(
    lambda t: np.cos(t),
    color=RED,
)
self.play(Create(sin_func))
self.play(Create(cos_func))

3.2. 函数的平移和缩放

这个示例展示了如何通过move_to和scale方法对函数图像进行平移和缩放操作。

通过这种方式，可以直观地展示函数图像的变换。

# 绘制原始函数图像
func = FunctionGraph(
    lambda t: np.sin(t),
    color=BLUE,
)

self.play(Create(func))
self.play(func.animate.move_to(UP))
self.play(func.animate.scale(0.5))

3.3. 复合函数图像

这个示例展示了如何绘制复合函数的图像。

通过将多个函数组合在一起，可以生成复杂的图像，用于展示函数的叠加效果。

# 绘制复合函数图像
composite_func = FunctionGraph(
    lambda t: np.sin(t) + 0.5 * np.sin(7 * t) + (1 / 7) * np.sin(14 * t),
    color=ORANGE,
)
self.play(Create(composite_func))

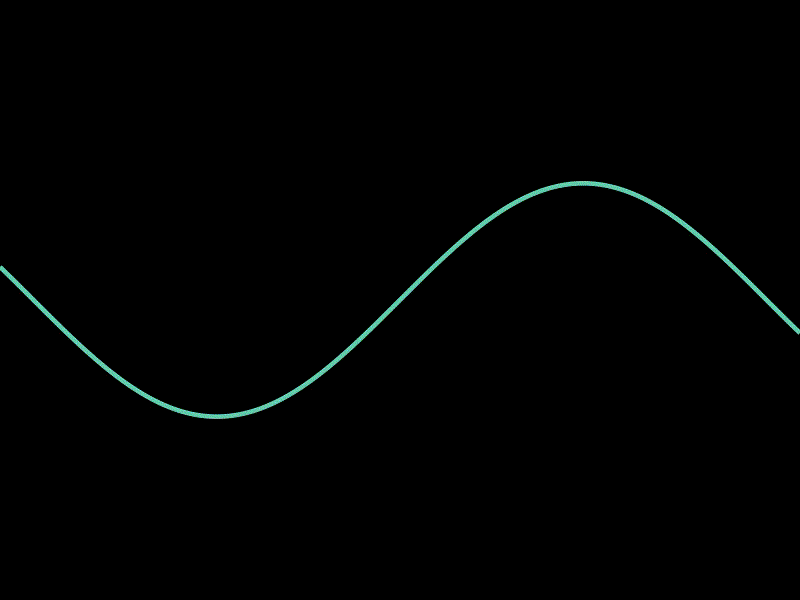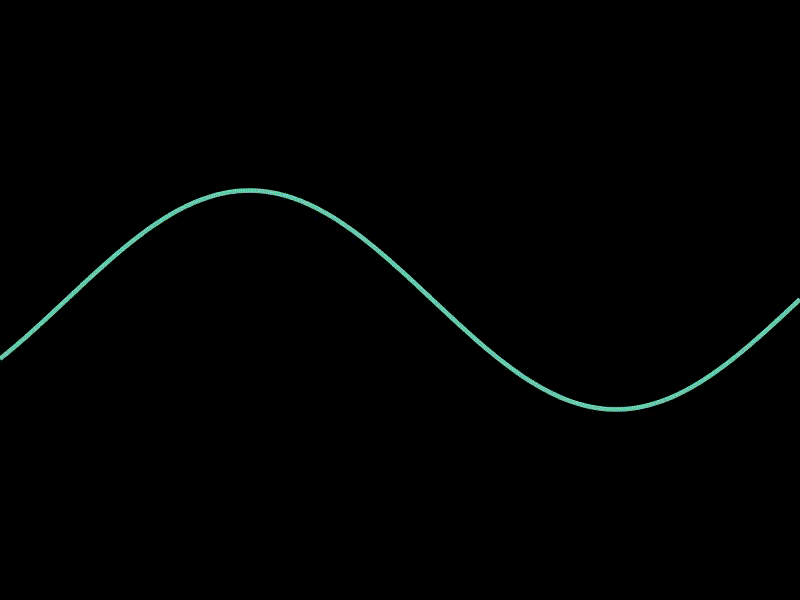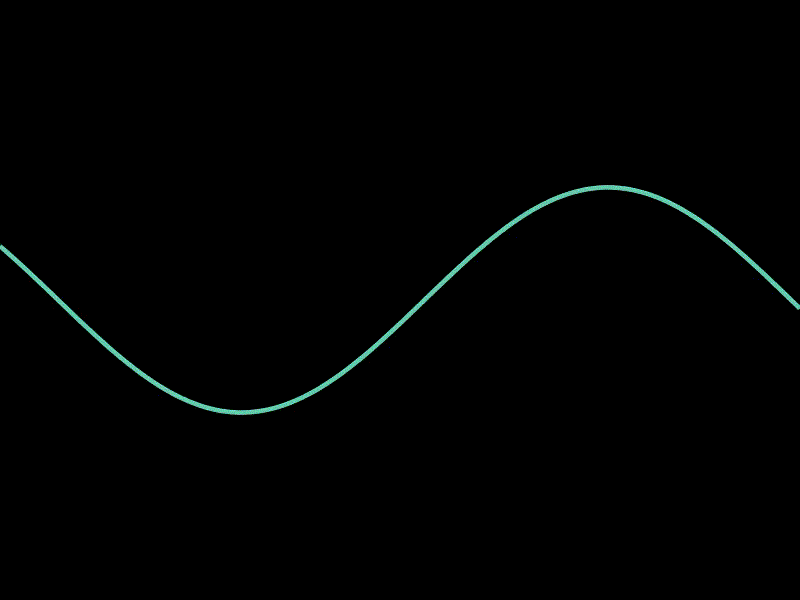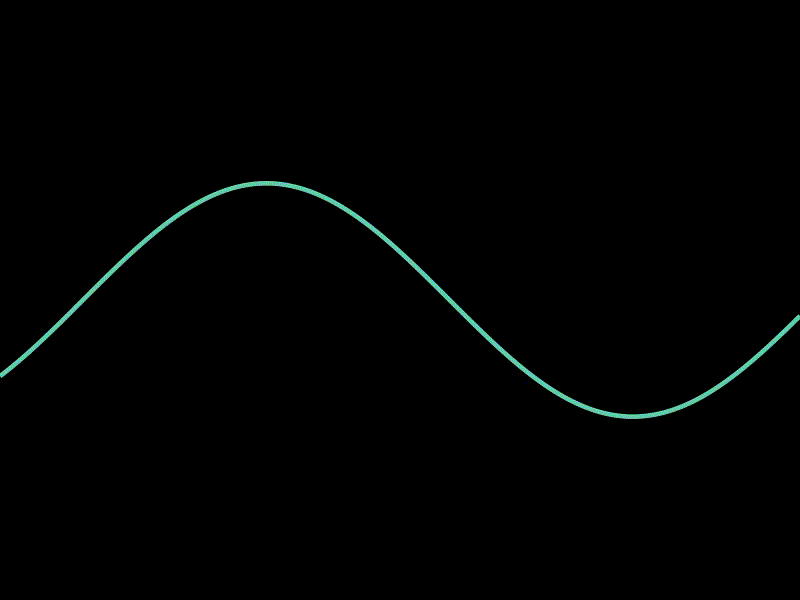
3.4. 动态展示函数图像的变化

这个示例展示了如何动态展示函数图像的变化。

通过在每一帧中更新函数的定义，可以实现函数图像的动态变化效果，非常适合用于展示函数随时间的变化。

# 定义一个动态变化的函数
def dynamic_func(t, time):
    return np.sin(t + time)

# 创建一个动态函数图像
dynamic_graph = FunctionGraph(
    lambda t: dynamic_func(t, 0),
    color=TEAL,
)
self.add(dynamic_graph)
# 动态更新函数图像
for time in range(10):
    new_graph = FunctionGraph(
        lambda t: dynamic_func(t, time),
        color=TEAL,
    )
    self.play(Transform(dynamic_graph, new_graph))