计算机中表示图与网络的方法有,第二章--网络与图(复杂网络学习笔记)

网络与图

图的定义

图的数学表示:\(G=(V, E)\)

节点数: \(N=|V|\), 边数\(M=|E|\)

图的类型

按照边的方向分为: 有向图和无向图

按照边的权值分为: 加权图和无权图

简单图

本书重点介绍无权无向图.

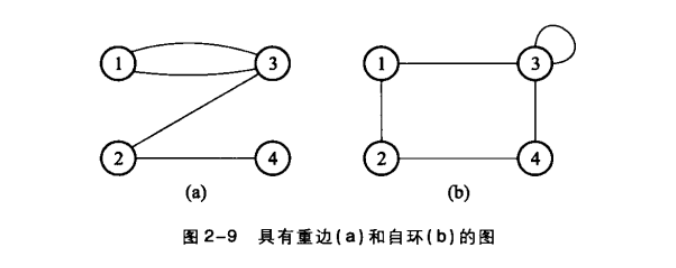
重边: 两个节点之间只有一条边

自环: 没有以同一个节点为起止点的边

简单图:没有重边且没有自环的图

如下图所示: 非简单图

简单图的两种极端情形:

空图(Null Graph): 它有两种定义,一是指没有任何节点和连边的图;二是指没有任何连边的图.

完全图(Complete Graph): 任意两个节点之间都有一条连边, 即边数为\(\frac{1}{2}N(N-1)\)

稀疏网络: 网络中的边数与\(N\)同阶

图的计算机表示

两种最常见的网络表示方法:邻接矩阵(Adjacency Matrix)和邻接表(Adjancency list)

1. 邻接矩阵

令有一个N个节点的图G, 那么其邻接矩阵大小为\(N*N\),其中元素为

\[a_{ij}=

\begin{cases}

w_{ij}& \text{节点i指向节点j的边的权值}\\

0& \text{节点i与节点j之间没有连边}

\end{cases}\]

如一个邻接矩阵: