面试场景题：如何设计一个抢红包随机算法

最新推荐文章于 2025-05-26 11:39:37 发布

江半

最新推荐文章于 2025-05-26 11:39:37 发布

阅读量33

点赞数

文章标签：面试算法 java 职场和发展开发语言

面试官：咱来写个算法题吧

设计一个抢红包的随机算法，比如一个人在群里发了100块钱的红包，群里有10个人一起来抢红包，每人抢到的金额随机分配。

1.所有人抢到的金额之和要等于红包金额，不能多也不能少。

2.每个人至少抢到1分钱。

3.最佳手气不超过红包总金额的90%

解题思路1：随机分配法

钱的单位转换为分，每次在[1, leaveMoney]这个区间内随机一个值，记为r；
计算一下剩余金额leaveMoney-r，剩余金额（单位：分）必须大于剩余人数，不然后面的人无法完成分配，例如10个人，有1个人抢了红包，剩余的money至少还需要9分钱，不然剩余的9人无法分；
按照顺序随机n-1次，最后剩下的金额可以直接当做最后一个红包，不需要随机；

解题代码：

 public static List<Double> generate(double totalMoney, int people) {
        // 转换为分处理避免浮点误差
        double totalCents = Math.round(totalMoney * 100);
        double maxLimit = (totalCents * 0.9); // 总金额的90%
        double leaveMoney = totalCents;
        List<Double> result = new ArrayList<>();
        //判断钱不够分,不处理
        if ((int)totalCents < people) {
            return result;
        }
        Random random = new Random();

        //每次生成随机数
        int n = people - 1;
        while (n > 0) {
            //随机数在[1, min(maxLimit, leaveMoney)]之间，单位是:分
            double min = Math.min(leaveMoney, maxLimit);
            double allocResult = 1 + random.nextInt((int)min);
            //判断这次分配后，后续的总金额仍然可分，且不超过90%总金额
            if (allocResult > maxLimit || (leaveMoney - allocResult) < n) {
                continue;
            }
            leaveMoney -= allocResult;
            n--;
            result.add(allocResult / 100.0);
        }
        result.add(leaveMoney / 100.0);
        return result;
    }

以下是多次运行的结果：

[37.77, 50.76, 1.89, 7.89, 0.26, 0.24, 0.25, 0.78, 0.06, 0.1]
[89.38, 2.45, 3.5, 4.43, 0.03, 0.08, 0.06, 0.04, 0.01, 0.02]
[53.51, 40.86, 5.48, 0.04, 0.06, 0.01, 0.01, 0.01, 0.01, 0.01]
[42.71, 0.27, 38.99, 4.5, 4.02, 4.58, 2.97, 0.84, 0.21, 0.91]

通过多次运行的结果，可以看到越早抢红包的人，抢到的金额越大，所以题目还可以变形

要求红包金额分布均衡

面试官：继续改进红包生成算法，要求：

1.要保证红包拆分的金额尽可能分布均衡，不要出现两极分化太严重的情况。

解题思路2：二倍均值法

二倍均值法：假设剩余红包金额为m元，剩余人数为n，那么有如下公式：

每次抢到的金额 = 随机区间 [0.01，m /n × 2 - 0.01]元

这个公式，保证了每次随机金额的平均值是相等的，不会因为抢红包的先后顺序而造成不公平。

举个例子如下：

假设有5个人，红包总额100元。100÷5×2 = 40，所以第1个人抢到的金额随机范围是[0.01，39.99]元，在正常情况下，平均可以抢到20元。

假设第1个人随机抢到了20元，那么剩余金额是80元。80÷4×2 = 40，所以第2个人抢到的金额的随机范围同样是[0.01，39.99]元，在正常的情况下，还是平均可以抢到20元。假设第2个人随机抢到了20元，那么剩余金额是60元。60÷3×2 = 40，所以第3个人抢到的金额的随机范围同样是[0.01，39.99]元，平均可以抢到20元。以此类推，每一次抢到金额随机范围的均值是相等的。

解题代码：

public static List<Double> allocateRedEnvelop(double totalMoney, int people) {
        // 转换为分处理避免浮点误差
        double totalCents = Math.round(totalMoney * 100);
        double maxLimit = (totalCents * 0.9); // 总金额的90%
        Random random = new Random();
        double leaveMoney = totalCents;
        List<Double> result = new ArrayList<>();
        int n = people;
        //注意是大于1，最后1个人领取剩余的钱
        while (n > 1) {
            //生成随机金额的范围是[1, leaveMoney / n * 2 - 1]， 注意nextInt方法生成结果范围是左闭右开的
            double allocatMoney = 1 + random.nextInt((int)leaveMoney / n * 2 - 1);
            result.add(allocatMoney / 100.0);
            n--;
            leaveMoney -= allocatMoney;
        }
        result.add(leaveMoney / 100.0);
        return result;
    }

生成结果测试如下，结果值比较随机了，领取的红包金额和先后顺序无关了

[8.58, 4.56, 20.88, 13.83, 7.6, 3.94, 10.87, 8.66, 20.92, 0.16]
[3.31, 2.08, 15.99, 16.79, 13.13, 0.61, 17.38, 10.93, 4.93, 14.85]
[0.24, 21.86, 15.57, 16.86, 3.45, 3.18, 5.48, 13.01, 6.76, 13.59]

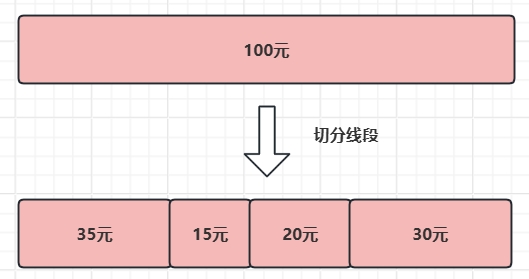
解题思路3：线段切割法

考虑一种新的解法，把红包总金额想象成一条很长的线段，而每个人抢到的金额就是这条主线段上的某个子线段，如下图：

假设有N个人一起抢红包，红包总金额为M，就需要确定N-1个切割点；
切割点的随机范围是（1，M），所有切割点确认后，子线段长度也就确定了
如果随机切割点出现重复，则重新生成切割点

解题代码如下：

    /**
     * 线段切割法
     */
    public static List<Double> allocateRedEnvelopNew(double totalMoney, int people) {
        // 转换为分处理避免浮点误差
        double totalCents = Math.round(totalMoney * 100);
        double maxLimit = (totalCents * 0.9); // 总金额的90%
        Random random = new Random();
        double leaveMoney = totalCents;
        List<Double> result = new ArrayList<>();
        Set<Integer> pointCutSet = new HashSet<>();
        int n = people;
        while (pointCutSet.size() < people - 1) {
            //生成n - 1个切割点，随机点取值范围是[1, totalCents]
            pointCutSet.add(random.nextInt((int) totalCents) + 1);
        }
        //接着生成对应子线段的钱数
        Integer[] points = pointCutSet.toArray(new Integer[0]);
        Arrays.sort(points);
        result.add(points[0] / 100.0);
        //子线段+ 最后那段的长度 = totalCents，注意上一步是已经加了points[0]，result中的所有元素和累加后的结果一定是totalCents,
        for (int i = 1; i < points.length; i++) {
            result.add((points[i] - points[i - 1]) / 100.0);
        }
        result.add((totalCents - points[points.length - 1]) / 100.0);
        return result;
    }

最后跑几次看看生成的随机效果，可以看到手气最佳的有到37块钱的，相比较二倍均值法，该方法手气最佳获取的金额可能更高

[20.24, 3.9, 7.63, 9.62, 15.41, 2.32, 0.21, 24.94, 9.66, 6.07]
[8.64, 33.55, 3.76, 15.35, 4.41, 9.85, 4.81, 15.9, 2.71, 1.02]
[11.31, 13.32, 16.53, 5.91, 8.69, 17.29, 11.09, 7.62, 7.14, 1.1]
[21.34, 8.24, 1.9, 7.98, 0.49, 0.32, 13.75, 37.27, 0.03, 8.68]

以上就是关于红包随机算法的所有解题方法了，面试中如果遇到考这道算法题，需要问清楚红包随机的情况，有没有要求分布均衡。

如果觉得对面试有帮助的话，记得给文章点赞哦~

原创作者: dnboy 转载于: https://www.cnblogs.com/dnboy/p/18781788