深入理解权值线段树

在上一篇探讨线段树的文章中 https://www.cnblogs.com/ofnoname/p/18625369，我们已经掌握了如何利用线段树高效处理数组区间查询与更新问题。这种经典线段树以数组下标为构建基础，完美解决了诸如区间求和、最值查询等典型场景。

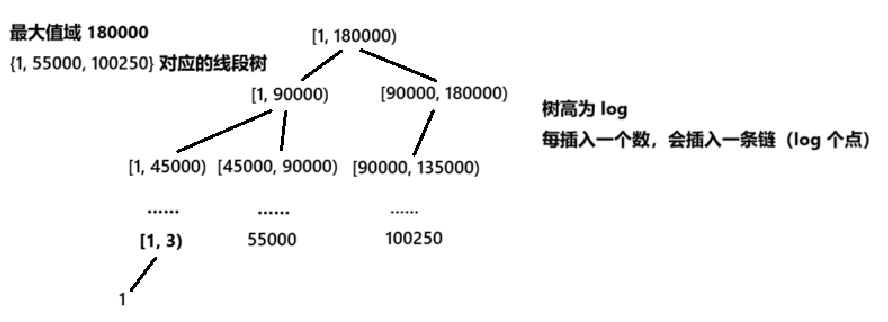
而线段树结构还有另外一个用处：想象这样一个场景：我们需要实时统计当前集合中数值在[L,R]范围内的元素个数，或者快速查询第K大的数值。此时，权值线段树（Weight Segment Tree）便闪亮登场——它巧妙的维护基础从"数组下标"转换为"值域空间"，开辟了线段树应用的新维度。

与常规线段树不同，权值线段树面临两个独特挑战：首先，值域范围可能非常庞大（如[1,1e9]），使得传统的数组存储方式变得不切实际；其次，值域分布往往极其稀疏（仅有少量离散点被使用）。这促使我们放弃静态的数组表示法，转而采用动态节点生成的指针表示法，只在必要时创建节点，从而大幅节省空间。

权值线段树的基本原理

从下标维护到值域维护

传统线段树维护的是数组下标区间的信息，例如：

• 区间和：$\text{sum}(l,r)={\sum }_{i=l}^r{a}_i$
• 区间最大值：$\max (l,r)=\max (a_l,a_{l+1},\dots ,a_r)$

而权值线段树（也称为值域线段树）维护的是数值的值域区间，例如：

• 数值在 $[L,R]$ 范围内的出现次数
• 整个集合中第 $K$ 小的数

二叉树的表示方法

线段树是一个二叉树。由于权值线段树的值域可能非常大（如 $[1,10^9]$），甚至稀疏（仅有少量数值被插入），我们无法像传统线段树那样使用固定数组存储，而必须采用动态节点生成的指针表示法：

数组表示法（静态存储）

• 适用于紧凑且值域较小的情况（如 $[1,N]$，$N\le 10^6$）
• 类似堆式存储，节点 $i$ 的左儿子是 $2i$，右儿子是 $2i+1$
• 缺点：如果值域很大（如 $[1,10^9]$），空间爆炸

指针表示法（动态开点）

• 仅在实际插入数值时才创建对应的节点
• 每个节点存储：
  • 值域区间 $[l,r]$
  • 统计信息（如出现次数 $cnt$，区间和 $sum$）
  • 左儿子 left 和右儿子 right 指针
• 优点：节省空间，仅 $O(M\log N)$，其中 $M$ 是操作次数，$N$ 是值域范围

关键点：

• 只有被访问过的区间才会生成节点
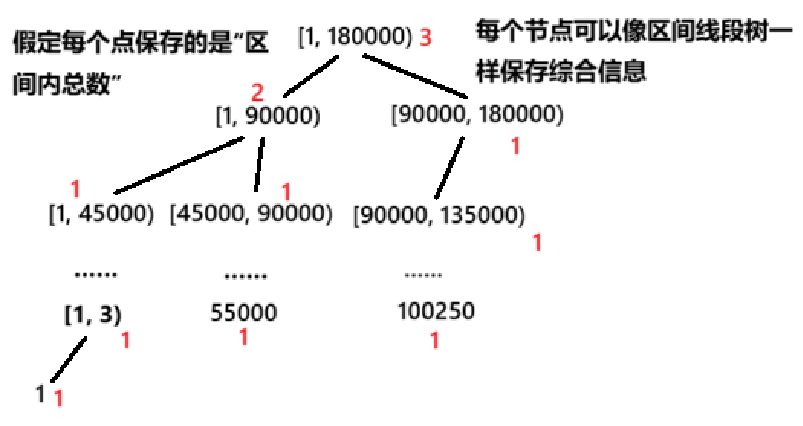
• 父节点的信息由其子节点汇总（如 cnt = left->cnt + right->cnt）

权值线段树的实现细节

节点结构设计

我们采用面向对象的方式定义权值线段树的节点结构：

   

       
struct Node {

       
    int l, r;       // 值域区间[l,r]

       
    int cnt;        // 该值域内数字出现次数

       
    int sum;        // 该值域内数字的和（可选）

       
    Node *left, *right; // 左右子节点指针

       
 

       
    Node(int _l, int _r) : l(_l), r(_r), cnt(0), sum(0), left(nullptr), right(nullptr) {}

       
};

核心操作：插入数值

每次插入一个数x时，我们从根节点开始递归更新线段树：

1. 如果当前节点的值域区间[l,r]不包含x，直接返回
2. 如果当前节点是叶子节点（l==r），更新统计信息
3. 否则递归处理左右子树，并动态创建不存在的子节点

   

       
void insert(Node* root, int x) {

       
    if (x < root->l || x > root->r) return;

       
    

       
    if (root->l == root->r) {

       
        root->cnt++;

       
        root->sum += x;

       
        return;

       
    }

       
    

       
    int mid = root->l + (root->r - root->l) / 2;

       
    if (x <= mid) {

       
        if (!root->left) root->left = new Node(root->l, mid);

       
        insert(root->left, x);

       
    } else {

       
        if (!root->right) root->right = new Node(mid + 1, root->r);

       
        insert(root->right, x);

       
    }

       
    

       
    // 更新父节点统计信息

       
    root->cnt = (root->left ? root->left->cnt : 0) 

       
              + (root->right ? root->right->cnt : 0);

       
    root->sum = (root->left ? root->left->sum : 0)

       
              + (root->right ? root->right->sum : 0);

       
}

查询值域统计

查询值域$[L,R]$内的数字个数（类似地可以查询和、最大值等）：

   

       
int query(Node* root, int L, int R) {

       
    if (!root || R < root->l || L > root->r) return 0;

       
    if (L <= root->l && root->r <= R) return root->cnt;

       
    return query(root->left, L, R) + query(root->right, L, R);

       
}

查询第K小的数

利用权值线段树可以高效查询第K小的数：

   

       
int kth(Node* root, int k) {

       
    if (root->l == root->r) return root->l;

       
    

       
    int left_cnt = root->left ? root->left->cnt : 0;

       
    if (k <= left_cnt) return kth(root->left, k);

       
    return kth(root->right, k - left_cnt);

       
}

内存管理

由于采用动态开点，需要手动管理内存以避免泄漏：

   

       
void clear(Node* root) {

       
    if (!root) return;

       
    clear(root->left);

       
    clear(root->right);

       
    delete root;

       
}

复杂度分析

时间复杂度分析

权值线段树的所有核心操作都遵循二叉树搜索模式，其时间复杂度主要取决于树的高度。设值域范围为$[1,N]$：

• 插入操作：每次插入需要从根节点递归到叶子节点，时间复杂度为$O(\log N)$
• 查询操作：
  • 区间统计查询：$O(\log N)$
  • 第K小查询：$O(\log N)$
• 删除操作（实现类似插入）：$O(\log N)$

值得注意的是，这里的 $N$ 是值域范围，而非元素个数。当值域极大时（如 $[1,10^{18}]$），可以通过离散化预处理将$N$降至元素数量级。

空间复杂度分析

权值线段树的空间消耗主要来自动态创建的节点：

• 最坏情况：每个操作都访问全新的路径，需要创建$O(\log N)$个新节点
• M次操作的空间消耗：$O(M\log N)$
• 优化技巧：
  • 惰性删除：标记删除而非立即回收节点
  • 内存池预分配：减少动态内存分配开销

下表对比了不同情况下的空间使用：

场景	空间复杂度	说明
静态数组实现	$O(N)$	值域较大时不可行
动态开点（最坏）	$O(M\log N)$	每次操作都访问新路径
动态开点（平均）	$O(K\log N)$	K为一个小于 M 的数

与离散化的配合使用

对于极大值域但数据较为稀疏，若允许离线，可以先进行离散化处理：

   

       
vector<int> nums = {5, 3, 7, 1e9}; // 原始数据

       
sort(nums.begin(), nums.end());

       
nums.erase(unique(nums.begin(), nums.end()), nums.end());

       
 

       
// 建立值到排名的映射

       
unordered_map<int, int> val2rank;

       
for (int i = 0; i < nums.size(); ++i) {

       
    val2rank[nums[i]] = i + 1; // 排名从1开始

       
}

       
 

       
// 此时权值线段树的值域可设为[1, nums.size()]

       
WeightSegmentTree tree(1, nums.size());

离散化后的优势：

1. 值域$N$从原始范围降至实际数据规模，此时可以改用区间线段树的四倍数组写法了。
2. 保持数值间的大小关系不变
3. 查询时需要先将查询边界值离散化

权值线段树 vs 平衡树

权值线段树和平衡树（如AVL树、红黑树）都可以解决以下常见问题：

• 动态插入/删除数值
• 查询第K小的数
• 统计值域区间内的元素个数
• 查询前驱/后继

但它们在实现方式和扩展性上存在本质差异：

功能实现方式对比

功能	权值线段树实现方式	平衡树实现方式
插入/删除	递归更新值域区间统计量	通过旋转操作维持平衡
第K小查询	利用子树节点数二分搜索	中序遍历或维护子树大小
前驱/后继查询	转化为值域边界查询	直接查找相邻节点
区间统计	天然支持区间求和/最值	需要额外维护统计信息

优先选择权值线段树当：

• 需要频繁查询第K小或区间统计
• 值域范围可离散化处理
• 需要可持久化或高维扩展
• 数据离线处理（预先知道值域）

优先选择平衡树当：

• 需要频繁插入/删除动态数据
• 需要有序遍历或范围迭代
• 处理非数值型数据或自定义比较
• 内存限制严格

原创作者: ofnoname 转载于: https://www.cnblogs.com/ofnoname/p/18823844