简介:PCA(主成分分析)是一种有效的数据降维技术,常用于人脸识别领域以减少特征维度,提取代表性特征,优化识别效率。本压缩包提供了PCA在人脸识别上的C++实现,包括源代码和用于训练与测试的数据集。通过详细步骤,如数据预处理、协方差矩阵计算、特征值分解和降维,学生可以掌握PCA算法的应用,并使用ORL数据库进行实验验证。 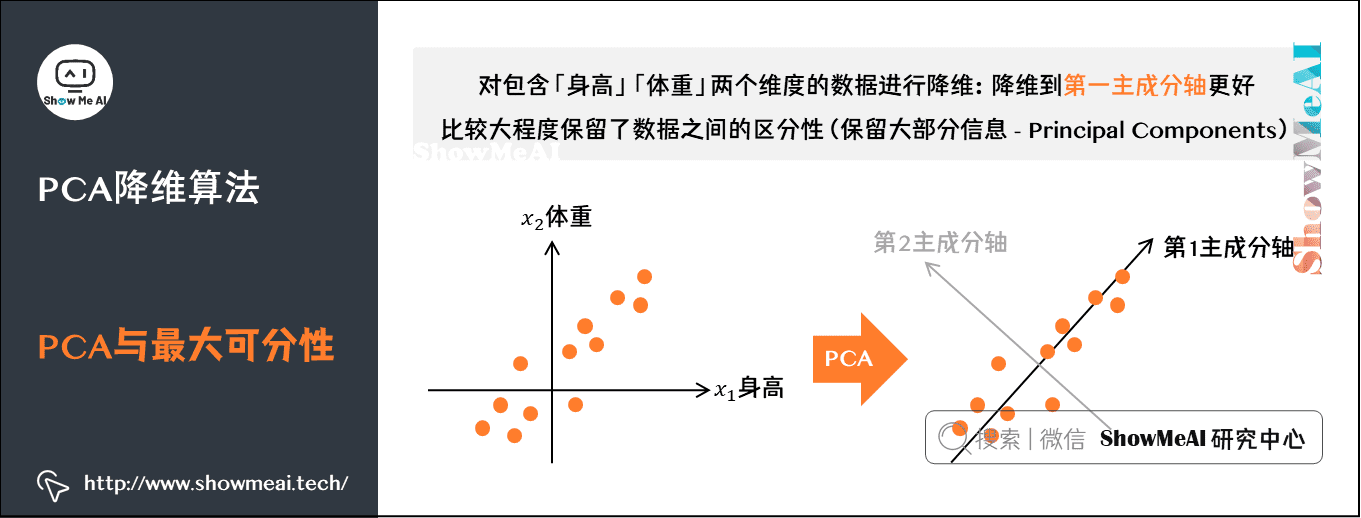
1. 数据降维技术PCA简介
在现代数据科学领域,数据降维技术起着关键作用,尤其是当面对高维数据时。主成分分析(PCA)是一种广泛使用的降维技术,它通过线性变换将原始数据转换为一组各维度线性无关的新变量,这些新变量称为主成分。PCA的主要目的是减少数据集的维度,同时保留尽可能多的数据变化信息。
PCA在数据压缩和可视化、去噪声、特征提取等领域有广泛应用。它的基本思想是通过正交变换将一组可能相关的变量转换为一组线性不相关的变量,这组新的变量称为主成分。每个主成分都是原始数据在不同方向上的投影,且这些方向是按照数据方差的大小顺序排列的。
然而,PCA并非万能,它在某些非线性结构的数据中可能不如其他降维技术有效。因此,在应用PCA之前,对数据进行合理的预处理,并理解PCA的降维机制和应用场景是至关重要的。接下来,我们将逐步探讨PCA的工作原理、应用案例以及与其它算法的比较,帮助读者深入理解并掌握PCA技术。
2. PCA算法细节理解与实验验证
在本章节中,我们将深入探讨PCA算法的理论细节,包括其数学基础和核心概念。然后,我们会通过实验步骤详细说明如何搭建实验环境、执行PCA算法,并最终分析实验结果。理解这些概念和步骤对于开发高效的人脸识别系统至关重要。
9.1 PCA算法的理论细节
9.1.1 PCA算法的数学基础
主成分分析(PCA)是一种线性降维技术,它通过正交变换将一组可能相关的变量转换成一组线性不相关的变量,称为主成分。PCA的数学基础涉及向量空间、协方差矩阵和特征值分解等概念。
PCA的基本步骤可概括为: - 数据中心化:通过减去数据的均值,使得数据的中心移至原点。 - 计算协方差矩阵:协方差矩阵描述了数据中各个维度之间的相关性。 - 特征值分解:找到协方差矩阵的特征向量和特征值,这些特征向量将构成新的空间的基。 - 选择主成分:依据特征值的大小选择最重要的k个特征向量,进行数据投影。
9.1.2 PCA算法的核心概念解读
在PCA中,主要概念包括特征向量、特征值、方差和协方差。特征向量表示数据在新空间中的方向,特征值表示每个特征向量的重要性。方差衡量数据在特征向量方向上的分散程度,协方差衡量不同特征向量间的相关性。
理解这些概念后,可以更好地把握PCA算法的工作原理。通过选择最重要的特征值对应的特征向量,PCA能够捕获数据中最重要的变化趋势,忽略掉不重要的部分。
9.2 PCA算法的实验步骤
9.2.1 实验环境的搭建和准备
为了验证PCA算法的效果,首先需要搭建一个合适的实验环境。这包括选择合适的编程语言和开发环境,安装必要的库文件,以及准备必要的数据集。
实验环境推荐: - 开发语言:Python、MATLAB或C++ - 数据处理库:NumPy、SciPy、OpenCV(针对C++) - 数据集:ORL数据集或其他人脸数据集
9.2.2 实验操作流程和注意事项
实验操作流程主要分为以下几个步骤: 1. 数据预处理:加载人脸数据集,进行中心化处理,确保数据适合PCA算法。 2. 协方差矩阵计算:基于处理后的数据计算协方差矩阵。 3. 特征值分解:对协方差矩阵进行特征值分解,提取特征向量和特征值。 4. 降维操作:根据特征值大小选取主要成分,将数据投影到新空间。 5. 结果分析:通过可视化等方法,分析降维前后的数据特性。
注意事项: - 确保数据预处理步骤正确无误,避免因数据错误影响实验结果。 - 在特征值分解时,注意特征值排序和选择主成分的数量。 - 对降维结果进行可视化,便于直观理解数据变化。
9.3 PCA算法的实验结果与分析
9.3.1 实验数据的收集和整理
在实验中,收集和整理实验数据是一个关键步骤。这包括记录每一步计算的关键数据,如特征值、特征向量、原始数据和降维后的数据等。这些数据将用于后续的结果分析和解读。
9.3.2 实验结果的分析和解读
在收集完数据后,需要对实验结果进行分析和解读。这可能包括: - 展示降维前后的数据对比图,以可视化形式展示数据压缩效果。 - 统计降维前后方差的保持程度,评估PCA降维的质量。 - 通过识别性能指标(如识别准确率)来评估PCA在人脸识别中的实际效果。
最终,通过对实验结果的深入分析,我们可以对PCA算法的有效性和适用性有一个准确的评价。这对于后续的研究和应用开发具有重要的指导意义。
3. C++实现PCA人脸识别程序
3.1 C++环境的搭建与配置
在本章节中,我们将介绍如何搭建和配置C++环境,这是实现PCA人脸识别程序的前提条件。
3.1.1 C++编译器的选择和安装
选择一个合适的C++编译器对于开发过程至关重要。编译器是将C++代码转换为计算机可执行指令的工具。目前市面上广泛使用的编译器包括GCC、Clang以及Microsoft的MSVC。对于跨平台开发,GCC和Clang是不错的选择;对于Windows平台,MSVC则更为合适。
GCC和Clang
GCC(GNU Compiler Collection)是支持多种编程语言的编译器集合,其中包含C++编译器g++。Clang是GCC的替代品,提供了更快的编译速度以及友好的错误信息。推荐安装GCC或Clang的最新稳定版本。
MSVC
MSVC(Microsoft Visual C++)是微软官方的C++编译器,与Visual Studio IDE紧密集成。在使用Visual Studio时,MSVC会自动安装,无需单独安装。
3.1.2 开发环境的配置方法
搭建好C++编译器后,还需要配置开发环境。常见的C++集成开发环境(IDE)有Visual Studio、CLion、Eclipse CDT等。选择一个符合个人开发习惯的IDE,可以有效提高开发效率。
Visual Studio配置
- 下载并安装Visual Studio。
- 在安装向导中选择“桌面开发”并安装C++开发工具。
- 打开Visual Studio,创建新项目并选择C++项目模板。
CLion配置
- 下载并安装CLion。
- 打开CLion,选择编译器路径(如果已经安装GCC或Clang)。
- 创建新项目,选择CMake或自定义项目模板。
Eclipse CDT配置
- 下载并安装Eclipse IDE。
- 安装Eclipse CDT(C/C++ Development Tooling)插件。
- 在Eclipse中配置C++编译器路径和项目。
一旦完成以上步骤,你的C++开发环境就已经搭建好了,可以开始PCA人脸识别程序的开发工作了。
3.2 PCA人脸识别程序的模块化设计
为了确保程序易于维护和扩展,我们将PCA人脸识别程序设计为模块化结构。
3.2.1 程序功能模块划分
PCA人脸识别程序主要分为以下几个模块:
- 图像处理模块:负责对输入的人脸图像进行必要的预处理。
- 主成分分析模块(PCA):执行PCA算法,提取主成分。
- 人脸识别模块:使用PCA提取的特征向量进行人脸的分类和识别。
- 用户界面模块:提供用户交互界面,用于输入图像、显示识别结果等。
3.2.2 程序框架搭建
在C++中,可以通过定义类和函数来搭建程序框架。
类和对象
-
ImageProcessor类:处理图像的类,包括加载、灰度化、尺寸调整等功能。 -
PCA类:实现PCA算法的类,负责计算协方差矩阵、求解特征值和特征向量。 -
FaceRecognizer类:负责使用PCA得到的特征向量进行人脸识别的类。 -
Application类:程序的主控制类,负责协调各个模块,处理用户输入。
函数和逻辑
每个类中可以包含多个函数,例如:
class ImageProcessor {
public:
void load_image(const std::string& path);
void convert_grayscale();
void resize_image(int width, int height);
// 其他图像处理相关函数...
};
class PCA {
public:
void compute_covariance(const Matrix& data);
Vector compute_eigenvectors();
// 其他PCA算法相关函数...
};
class FaceRecognizer {
public:
bool recognize(const Vector& feature_vector);
// 其他识别相关函数...
};
class Application {
public:
void run();
// 其他应用程序控制相关函数...
};
通过上述模块划分和程序框架搭建,我们为PCA人脸识别程序奠定了基础结构,接下来将详细介绍每个模块的具体实现。
3.3 PCA人脸识别程序的编码实现
编码实现是本章节的核心,接下来将具体介绍PCA算法核心以及用户界面的开发。
3.3.1 核心算法的编码
PCA算法的核心包括数据预处理、协方差矩阵计算、特征值分解以及降维。我们通过编写类方法来实现这些步骤。
数据预处理
void ImageProcessor::convert_grayscale() {
// 实现灰度化转换,将图像矩阵的每个像素值转换为灰度值
}
协方差矩阵计算
void PCA::compute_covariance(const Matrix& data) {
// 基于输入数据计算协方差矩阵
}
特征值分解
Vector PCA::compute_eigenvectors() {
// 基于协方差矩阵计算特征值和特征向量
}
降维
Matrix PCA::reduce_dimensionality(int k) {
// 通过特征值分解结果,进行数据降维至k维
}
3.3.2 用户交互界面的开发
用户交互界面允许用户选择图像、展示识别结果,并允许用户进行其他控制。
void Application::run() {
// 主循环
while (true) {
std::string input_path = get_user_input();
Image image = ImageProcessor().load_image(input_path);
Matrix data = preprocess_image(image);
PCA pca;
***pute_covariance(data);
Matrix reduced_data = pca.reduce_dimensionality(100);
FaceRecognizer recognizer;
bool is_recognized = recognizer.recognize(reduced_data);
display_result(is_recognized);
}
}
通过上述代码,用户可以通过程序的主函数与PCA人脸识别程序进行交互,进行人脸图像的选择、预处理、PCA降维以及识别结果的展示。
这样,我们就完成了PCA人脸识别程序的模块化设计和编码实现。接下来的章节,我们将对PCA算法的数学原理进行详细的阐述。
4. 数据预处理步骤
数据预处理是机器学习和模式识别任务中至关重要的一步,它直接影响到后续算法的学习效率和模型的准确性。在PCA人脸识别项目中,数据预处理尤为重要,因为它能减少噪声对模型的影响,提高识别的准确性。
4.1 人脸图像数据的采集与存储
4.1.1 数据采集的方法和工具
在进行人脸识别系统开发之前,首要的任务是从不同角度和条件下采集人脸图像数据。采集过程需要考虑多种因素,包括光照条件、表情变化、角度偏移和遮挡情况等。对于大规模数据集的构建,这些因素更需要细致考虑。
使用专业的图像采集工具,例如高分辨率摄像头,可以提高图像质量。同时,采集软件应能记录人脸的多角度和多表情图像,并且能够同步采集人脸的多种特征信息,如年龄、性别、种族等。
4.1.2 数据存储格式的选择
数据存储格式的选择对项目后期的数据处理和分析具有重要的影响。在PCA人脸识别项目中,图像数据通常以矩阵形式存储,常见的图像存储格式有:
- TIFF格式 :能够存储高分辨率图像,支持无损压缩,适合于细节丰富的图像数据。
- JPEG格式 :广泛使用,有损压缩,能有效减小文件大小,但可能会损失一些图像质量。
- PNG格式 :支持无损压缩,保持图像质量,支持透明度通道,适用于需要透明背景的图像处理。
考虑到预处理和存储效率,通常推荐使用PNG或TIFF格式。存储结构应该方便后续的快速访问和处理,例如可以采用数据库形式存储图像文件路径和其元数据。
4.2 图像数据的预处理方法
4.2.1 图像灰度化和二值化
图像灰度化是将彩色图像转换为灰度图像的过程,这样可以减少后续处理的数据量。图像的灰度值通常由R、G、B三个颜色通道的加权平均计算得出。灰度化操作可以通过设置一个阈值,将像素值高于阈值的设置为1(白色),低于阈值的设置为0(黑色),这个过程被称为二值化。
4.2.2 图像去噪和增强技术
图像噪声是影响人脸识别准确性的重要因素。常用的去噪技术包括:
- 中值滤波 :通过取周围像素的中值来替换中心像素,能够很好地去除椒盐噪声,同时保持边缘信息。
- 高斯滤波 :使用高斯核对图像进行卷积操作,适用于高斯噪声的去除。
图像增强技术,如直方图均衡化,能够提升图像的对比度,让图像更清晰。它通过重新分配图像中像素的强度值,来扩展整个图像的动态范围,进而改善图像的总体可视效果。
4.3 数据集的划分与标签标注
4.3.1 训练集、验证集和测试集的划分
在机器学习项目中,将数据集划分为训练集、验证集和测试集是必不可少的步骤。一般而言,训练集用于模型的训练,验证集用于调整模型的超参数,测试集用于评估模型的最终性能。
划分比例可以根据具体任务和数据集的大小进行调整。例如,可以将数据集按照70%、15%、15%的比例划分为训练集、验证集和测试集。
4.3.2 标注数据的预处理与管理
在监督学习中,标签的正确性直接影响模型训练的效果。因此,对标签的预处理和管理也非常重要。对于图像数据,标签可能包括识别对象的ID、姓名、表情、姿态等信息。为了便于管理,可以采用结构化的方式存储这些信息,如使用JSON格式或数据库表格形式。
此外,对于数据不平衡问题,可以采取过采样少数类、欠采样多数类等方法来平衡数据集,以减少模型训练的偏差。
通过上述步骤的细致处理,数据预处理阶段为PCA人脸识别模型提供了高质量和格式规范的输入数据。这将为后续的降维和特征提取工作打下坚实的基础。在下一章节中,我们将进一步探讨PCA算法的数学原理和实现细节。
5. 协方差矩阵计算方法
5.1 协方差矩阵的数学定义
5.1.1 协方差矩阵的基本概念
在统计学中,协方差矩阵是衡量多个随机变量之间线性关系的矩阵。假设有 n 个随机变量 X1, X2, ..., Xn ,协方差矩阵 Σ 是由这些随机变量两两之间的协方差构成的 n×n 矩阵。对于任意两个随机变量 Xi 和 Xj ,它们的协方差定义为:
 是 Xi 和 Xj 的协方差, σi^2 是 Xi 的方差。当 i=j 时,对角线元素表示 Xi 的方差。
5.1.2 协方差矩阵的几何意义
协方差矩阵的几何意义与向量空间中的概念紧密相关。对于一组数据点,协方差矩阵可以看作是数据在各维度上的分布情况的一种描述。如果两个维度的协方差为正,这意味着这两个维度上的数据有正向的相关性,即一个维度的值增加时,另一个维度的值也倾向于增加;如果协方差为负,则表示负向的相关性;而如果协方差为零,则表示两个维度上的数据变化相互独立。
5.2 协方差矩阵的计算步骤
5.2.1 协方差的计算公式
计算协方差矩阵的第一步是计算任意两个随机变量之间的协方差。考虑到我们通常处理的是样本数据而非整个总体,因此使用样本协方差来估计总体协方差。给定一组 m 个样本数据点,每个数据点有 n 个特征,样本协方差计算公式为:
。
- 对于每个维度与自身的计算结果,即为该维度的方差。
- 构造一个
n×n的矩阵,其中对角线元素为各维度的方差,非对角线元素为对应的协方差。
5.3 协方差矩阵的性质分析
5.3.1 协方差矩阵的对称性
协方差矩阵是一个对称矩阵。这是由于协方差的定义是 Cov(Xi, Xj) = Cov(Xj, Xi) ,即两个随机变量之间的协方差与顺序无关。因此,协方差矩阵中的第 (i, j) 元素和第 (j, i) 元素是相等的。这种对称性意味着协方差矩阵可以存储在下三角或上三角矩阵中,节省一半的存储空间。
5.3.2 协方差矩阵的正定性
协方差矩阵通常是正定的,这表示所有可能的特征值都是正数。正定矩阵的定义是对于任何非零向量 v ,都有 vTΣv > 0 。正定性说明了协方差矩阵在数学上具有良好的性质,例如可以被分解为一个唯一的特征值分解。这意味着对于任何随机变量集合,协方差矩阵总是可以提供关于变量间关系的有效信息。
为了在实际中计算协方差矩阵,我们可以采用编程语言中的统计库来简化这一过程。例如,在Python中可以使用 numpy 库来实现这一计算。以下是一个简单的Python代码示例:
import numpy as np
# 假设我们有一组样本数据,每一行是一个样本点,每一列是一个特征
samples = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
# 计算协方差矩阵
covariance_matrix = np.cov(samples, rowvar=False)
print("协方差矩阵为:")
print(covariance_matrix)
该代码片段首先导入 numpy 库,然后定义了一个样本数据集。使用 numpy 的 cov 函数计算协方差矩阵,并打印结果。在这个例子中, rowvar=False 参数指定了每一列是一个独立的变量,这是为了适应 numpy 的默认行为(即每一行是一个样本点,每一列是一个变量)。
通过此方法,我们能够获得数据特征之间的相关性,并进一步使用这些信息进行数据的降维处理,例如主成分分析(PCA)中。
6. 特征值分解过程
特征值分解是主成分分析(PCA)中非常关键的一个步骤,它有助于我们理解数据的本质特征和结构。本章节将详细介绍特征值和特征向量的定义、特征值分解的数学原理以及它在PCA中的应用。
6.1 特征值和特征向量的定义
6.1.1 特征值和特征向量的基本概念
在数学中,特征值和特征向量是线性代数中的重要概念,广泛应用于数据降维、图像处理、机器学习等领域。对于一个给定的方阵( A ),如果存在非零向量( v )和常数( \lambda ),满足以下等式:
[ A \cdot v = \lambda \cdot v ]
那么,标量( \lambda )被称为矩阵( A )的一个特征值,向量( v )被称为对应于( \lambda )的特征向量。直观来看,特征向量在矩阵变换后,仅在长度上发生伸缩,方向保持不变。
6.1.2 特征值分解的物理意义
特征值分解的物理意义在于,它可以揭示矩阵变换的本质,即变换前后数据的主要变化趋势。特征值告诉我们,在这个变换中,哪些方向上的数据变化被放大了(大的特征值对应的方向),哪些方向上的变化被缩小了(小的特征值对应的方向)。而特征向量则是这些方向的具体表述。
6.2 特征值分解的数学原理
6.2.1 特征值分解的数学方法
对于一个( n \times n )的矩阵( A ),其特征值分解可以表示为:
[ A = PDP^{-1} ]
其中,( P )是由( A )的( n )个线性无关的特征向量组成的矩阵,( D )是一个对角矩阵,对角线上的元素为( A )的特征值。( P^{-1} )是( P )的逆矩阵。
6.2.2 对称矩阵特征值分解的性质
如果矩阵( A )是对称矩阵,那么其特征值分解有特别重要的性质。对称矩阵的特征值都是实数,特征向量互相正交,并且可以标准化为一组标准正交基。因此,对称矩阵的特征值分解通常可以表示为:
[ A = Q\Lambda Q^T ]
这里,( Q )是由( A )的特征向量组成的正交矩阵,( \Lambda )是对角线上元素为特征值的对角矩阵,( Q^T )是( Q )的转置。
6.3 特征值分解在PCA中的应用
6.3.1 从协方差矩阵到特征值分解
在PCA中,特征值分解通常应用于协方差矩阵。协方差矩阵的特征值分解可以揭示数据集的内在结构,因为这个矩阵反映的是各个特征之间的相关性。
6.3.2 特征值分解在降维中的作用
当我们对协方差矩阵进行特征值分解后,得到的特征值可以告诉我们每个主成分(对应特征向量)的重要程度。在降维时,我们通常会选择那些对应的特征值较大的主成分。这是因为,大特征值意味着对应的特征向量方向上数据变化剧烈,包含了较多的原始信息。通过保留这些方向上的信息,可以最大程度地保留数据的结构和特征。
为了更好地理解特征值分解在PCA降维中的具体应用,我们可以采用以下步骤:
- 计算协方差矩阵 :首先计算样本数据的协方差矩阵。
- 特征值分解 :对协方差矩阵进行特征值分解。
- 选择特征向量 :根据特征值的大小,选择前( k )个最大的特征值对应的特征向量。
- 构造降维矩阵 :将所选特征向量作为列向量构造新的矩阵( P )。
- 转换数据空间 :用( P )转换原始数据,得到降维后的数据集。
通过以上步骤,我们可以有效地利用特征值分解将原始数据集降维到更有意义的子空间。这不仅简化了数据结构,而且有助于后续的数据分析和处理。
7. PCA降维技术实现
7.1 PCA降维的步骤和原理
7.1.1 数据中心化处理
PCA降维的第一步是将数据进行中心化处理,即将数据的均值调整为零。这是为了消除数据量纲的影响,确保各个特征维度之间的公平性。中心化处理可以通过以下步骤实现:
// 假设dataMatrix是一个二维数组,存储了所有的数据样本
// dataMatrix的每一行代表一个样本,每一列代表一个特征维度
int num_samples = dataMatrix.rows;
int num_features = dataMatrix.cols;
Eigen::MatrixXd centered = dataMatrix.rowwise() - dataMatrix.colwise().mean();
在上述代码中, Eigen::MatrixXd 是一个用于表示二维数组的矩阵类型, rowwise() 和 colwise() 方法分别表示按行和按列进行操作。 mean() 函数计算每一列(特征维度)的均值,并且整个矩阵的每一行(样本)都会减去这个均值,实现中心化。
7.1.2 降维的数学原理和步骤
中心化处理后,我们得到了零均值的数据矩阵。接下来是PCA降维的核心步骤:
- 计算数据的协方差矩阵,以捕捉特征之间的相关性。
- 对协方差矩阵进行特征值分解,得到特征值和特征向量。
- 选择最重要的特征向量,根据需要降维到指定的维度。
- 将原始数据投影到这些特征向量上,得到降维后的数据表示。
7.2 PCA降维技术的代码实现
7.2.1 实现降维函数的C++代码
在C++中,我们使用Eigen库来实现PCA降维。以下是实现降维函数的示例代码:
#include <iostream>
#include <Eigen/Dense>
#include <vector>
// 定义一个函数,实现PCA降维
Eigen::MatrixXd PCA_DimensionalityReduction(const Eigen::MatrixXd& dataMatrix, int reducedDim) {
// 计算协方差矩阵
Eigen::MatrixXd covMatrix = (dataMatrix.adjoint() * dataMatrix) / double(dataMatrix.rows() - 1);
// 特征值分解
Eigen::SelfAdjointEigenSolver<Eigen::MatrixXd> eigensolver(covMatrix);
if (***() != Eigen::Success) {
std::cerr << "Eigenvalue decomposition failed!" << std::endl;
return Eigen::MatrixXd();
}
// 获取特征值和特征向量
Eigen::VectorXd eigenValues = eigensolver.eigenvalues();
Eigen::MatrixXd eigenVectors = eigensolver.eigenvectors();
// 获取前reducedDim个特征值和特征向量
Eigen::MatrixXd topEigenvectors = eigenVectors.rightCols(reducedDim);
// 将数据投影到选定的特征向量上
Eigen::MatrixXd reducedData = dataMatrix * topEigenvectors;
return reducedData;
}
// 主函数用于演示如何调用上述PCA降维函数
int main() {
// 假设dataMatrix是一个已经中心化的数据矩阵
Eigen::MatrixXd dataMatrix; // 这里应该是初始化好的数据矩阵
// 指定希望降到的维度
int reducedDim = 50;
// 执行PCA降维
Eigen::MatrixXd reducedData = PCA_DimensionalityReduction(dataMatrix, reducedDim);
// 输出降维后的数据维度
std::cout << "Reduced data matrix dimensions: " << reducedData.rows() << " x " << reducedData.cols() << std::endl;
return 0;
}
7.2.2 降维效果的验证方法
验证PCA降维效果的一个常用方法是可视化。可以使用散点图或热图来观察降维前后的数据分布。在C++中,可以将降维后的数据导出到文件,并使用Python的matplotlib库进行可视化。
7.3 人脸特征提取与识别模型构建
7.3.1 提取人脸特征的方法
在PCA降维的基础上,我们可以提取人脸图像的特征。人脸特征提取是通过将图像数据投影到PCA空间中,然后选择最重要的特征值对应的特征向量来表示每一个人脸图像。
7.3.2 构建基于PCA的人脸识别模型
基于PCA的人脸识别模型构建需要以下几个步骤:
- 将训练集中的每个人脸图像都投影到PCA空间中,形成一个人脸特征空间。
- 对于验证集或测试集中的每个人脸图像,也执行相同的投影操作。
- 将投影得到的特征向量与训练集中的人脸特征向量进行比较,采用某种距离度量(如欧氏距离)来找出最相似的训练样本。
在实际的模型构建过程中,还需要考虑如何处理光照变化、表情变化等因素,以提高模型的泛化能力和识别准确率。
简介:PCA(主成分分析)是一种有效的数据降维技术,常用于人脸识别领域以减少特征维度,提取代表性特征,优化识别效率。本压缩包提供了PCA在人脸识别上的C++实现,包括源代码和用于训练与测试的数据集。通过详细步骤,如数据预处理、协方差矩阵计算、特征值分解和降维,学生可以掌握PCA算法的应用,并使用ORL数据库进行实验验证。





















 724
724

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








