《代码随想录》回溯问题学习总结

How to work out the problem of backtracing?

1. 组合问题

回溯的本质仍然是递归
考虑递归三部曲:

1. 递归传递参数和返回值 backtracing() -> None:
2. 递归的结束条件
3. 在每次递归中需要执行的逻辑

---

1.1 分析回溯问题

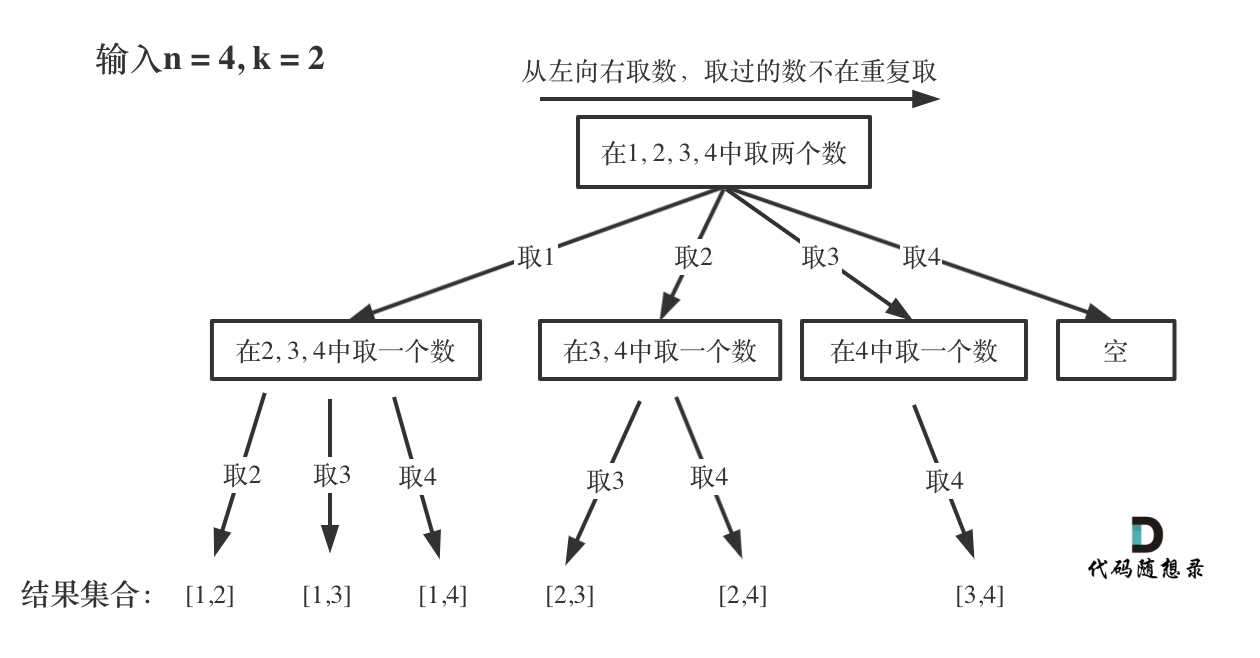
以最简单的组合问题为例，在抽象树的每一层中是遍历每种可能取值，而在树枝（深度）中遍历则是寻找每种组合的子组合

1.2 回溯问题的模版代码

仍然组合问题为例

# 组合问题
def combine(self, n: int, k: int) -> list[list[int]]:
    result = []
    self.backtracing(n, k, 1, [], result)
    return result

# paragram
def backtracing(self, n, k, startindex, path: list, result: list):
    # stop condition
    if len(path) == k:
        result.append(path[:])
        return
    
    for i in range(startindex, n - (k - len(path)) + 2): # 剪枝
        path.append(i)
        self.backtracing(n, k, i+1, path, result)
        path.pop()

1.3 什么时候需要startindex

每次在集合中选取元素，可选择的范围随着选取的进行而收缩（可选取元素减少），调整可选取的范围，就是要靠startindex

1.4 在for - 层遍历过程中添加额外判断逻辑

以Leetcode第40题组合总和为例，需要对元素进行去重

    # LC.40.组合总和2
def combinationSum2(self, candidates: list[int], target: int) -> list[list[int]]:
    candidates = sorted(candidates)
    temp, res = [], []

    def backtracing(startindex: int, used: list) -> None:
        
        if target == sum(temp):
            res.append(temp.copy())
            return
        
        elif target < sum(temp):
            return
            

        for i in range(startindex, len(candidates)):
            if i > 0 and candidates[i-1] == candidates[i] and used[i-1] == False:
                continue

            temp.append(candidates[i])
            used[i] = True
            backtracing(i+1, used)
            used[i] = False
            temp.pop()
    
    backtracing(0, [False for i in range(len(candidates))])

在本题中，同一个解可以出现同一元素（按树枝搜索），但在解集合中不能出现相同元素，如[[1,1,2],[1,2,1]]是不合法的，使用candidates[]与used[]数组来控制按层搜索和按树枝搜索时出现重复元素是否可以被添加到解集合中，体现在代码中：

for i in range(startindex, len(candidates)):
        if i > 0 and candidates[i-1] == candidates[i] and used[i-1] == False:
            continue

2. 子集问题

2.1 子集问题概述

子集问题和排列问题的不同之处是需要收集抽象树上的每一个节点，而非叶子节点。即每次回溯都需要判断当前节点是否是解，而非在每次回溯判断是否到达叶子节点。

2.2 子集问题模版

以力扣第70题为例，在每次调用backtracing()函数后都需要收集当前节点

def subsets(self, nums: list[int]) -> list[list[int]]:
    res, path = [], []

    # 回溯
    def backtracing(startindex: int) -> None:
        # 每次调用backtracing都是在遍历该树的一个节点
        res.append(path.copy())

        if startindex == len(nums):
            return
        
        for i in range(startindex, len(nums)):
            path.append(nums[i])
            backtracing(i+1)
            path.pop()
    
    backtracing(0)
    return res

2.3 子集问题去重

子集问题的去重同组合问题相同，但需要对集合进行排序，考虑在抽象树的每一数层上不可以使用相同元素，以力扣第90题为例，分别使用used标志数组和set()集合去重

2.3.1 used标志数组去重

# 去重问题，同一树层不能重复（不同的解集合），但在同一树枝可以重复（寻找唯一子集的过程，树的遍历深度加深）
def subsetsWithDup(self, nums: list[int]) -> list[list[int]]:
    nums.sort()
    res, path = [], []


    # 回溯
    def backtracing(startindex: int, used: list[bool]) -> None:
        # 每次调用backtracing都是在遍历该树的一个节点
        res.append(path.copy())

        if startindex == len(nums):
            return
        
        for i in range(startindex, len(nums)):
            # 去重
            if i > 0 and nums[i-1] == nums[i] and used[i-1] is False:
                continue

            path.append(nums[i])
            used[i] = True
            backtracing(i+1, used)
            # 回溯
            used[i] = False
            path.pop()
    
    backtracing(0, [False for i in range(len(nums))])
    return res

2.3.2 set()集合去重

def subsetsWithDup(self, nums):
    nums.sort()  # 去重需要排序
    result = []
    self.backtracking(nums, 0, [], result)
    return result

def backtracking(self, nums, startIndex, path, result):
    result.append(path[:])
    used = set()
    for i in range(startIndex, len(nums)):
        if nums[i] in used:
            continue
        used.add(nums[i])
        path.append(nums[i])
        self.backtracking(nums, i + 1, path, result)
        path.pop()

3. 排列问题

3.1 概述

排列问题与组合问题的区别在于每次for循环遍历时不使用startindex来寻找下一个遍历起始位置，而是从0开始

3.2 模版

def permute(self, nums: list[int]) -> list[list[int]]:
    res, path = [], []

    def backtracing() -> None:
        if len(path) is len(nums):
            res.append(path.copy())
            return
        
        for i in range(len(nums)):
            # 数字不重复
            if nums[i] in path:
                continue

            path.append(nums[i])
            backtracing()
            path.pop()

    backtracing()
    return res

3.3 去重

去重逻辑和之前相同，但需要注意的是，在同一树枝上进行遍历时也需要去重，即使用if used[i] == Fasle来避免在同一树枝进行遍历时使用到相同元素如nums=[1,1,2]中，选取顺序：nums[0], nums[1], nums[2]与nums[1], nums[0], nums[2]会导致排列集重复

def permuteUnique(self, nums: list[int]) -> list[list[int]]:
    nums.sort()
    res, path = [], []

    def backtracing(used: list) -> None:
        if len(path) is len(nums):
            res.append(path.copy())
            return
        for i in range(len(nums)):
            if (i > 0 and nums[i-1] == nums[i] and not used[i-1]):
                continue

            if used[i] == False: # 同一树枝i没使用过
                used[i] = True
                path.append(nums[i])
                backtracing(used)
                path.pop()
                used[i] = False

    backtracing([False for i in range(len(nums))])
    return res

原创作者: yunshengbuzhichu 转载于: https://www.cnblogs.com/yunshengbuzhichu/p/18950205