k-means 算法是一种基于划分的聚类算法,它以 k 为参数,把 n 个数据对象分成 k 个簇,使簇内具有较高的相似度,而簇间的相似度较低。
1. 基本思想
k-means 算法是根据给定的 n 个数据对象的数据集,构建 k 个划分聚类的方法,每个划分聚类即为一个簇。该方法将数据划分为 n 个簇,每个簇至少有一个数据对象,每个数据对象必须属于而且只能属于一个簇。同时要满足同一簇中的数据对象相似度高,不同簇中的数据对象相似度较小。聚类相似度是利用各簇中对象的均值来进行计算的。
k-means 算法的处理流程如下。首先,随机地选择 k 个数据对象,每个数据对象代表一个簇中心,即选择 k 个初始中心;对剩余的每个对象,根据其与各簇中心的相似度(距离),将它赋给与其最相似的簇中心对应的簇;然后重新计算每个簇中所有对象的平均值,作为新的簇中心。
不断重复以上这个过程,直到准则函数收敛,也就是簇中心不发生明显的变化。通常采用均方差作为准则函数,即最小化每个点到最近簇中心的距离的平方和。
新的簇中心计算方法是计算该簇中所有对象的平均值,也就是分别对所有对象的各个维度的值求平均值,从而得到簇的中心点。例如,一个簇包括以下 3 个数据对象 {(6,4,8),(8,2,2),(4,6,2)},则这个簇的中心点就是 ((6+8+4)/3,(4+2+6)/3,(8+2+2)/3)=(6,4,4)。
k-means 算法使用距离来描述两个数据对象之间的相似度。距离函数有明式距离、欧氏距离、马式距离和兰氏距离,最常用的是欧氏距离。
k-means 算法是当准则函数达到最优或者达到最大的迭代次数时即可终止。当采用欧氏距离时,准则函数一般为最小化数据对象到其簇中心的距离的平方和,即
 。
。
其中,k 是簇的个数,
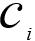 是第 i 个簇的中心点,dist(
是第 i 个簇的中心点,dist(
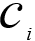 ,x)为 X 到
,x)为 X 到





 本文介绍了k-means聚类算法的基本思想和处理流程,通过计算数据对象与簇中心的相似度进行划分。在Spark MLlib中,k-means算法有多个参数可调,如最大迭代次数、初始中心选择方式等。通过KMeans.train方法训练模型,然后使用KMeansModel.predict进行预测。文章还展示了k-means算法的实例,以及算法的优缺点,包括对初始值和簇个数的依赖、对异常值的敏感性以及对非凸形状簇的识别问题。
本文介绍了k-means聚类算法的基本思想和处理流程,通过计算数据对象与簇中心的相似度进行划分。在Spark MLlib中,k-means算法有多个参数可调,如最大迭代次数、初始中心选择方式等。通过KMeans.train方法训练模型,然后使用KMeansModel.predict进行预测。文章还展示了k-means算法的实例,以及算法的优缺点,包括对初始值和簇个数的依赖、对异常值的敏感性以及对非凸形状簇的识别问题。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








