递归函数问题_递归函数

递归函数问题

Recursion is an important concept in computer science. It is a programming technique that involves a function repeatedly calling itself until it reaches a solution. A recursive function, then, is a function that calls itself.

递归是计算机科学中的重要概念。 它是一种编程技术，涉及一个函数反复调用自身直到达到解决方案。 那么， 递归函数就是一个调用自身的函数。

A recursive function involves a recursive call and a base case. A recursive call is the part of the function body that calls itself until a specified condition is met, while the base case is the function’s stopping point. It is important that we have a base case because without it, we would be stuck in an infinite loop. The Educative diagram below is helpful in understanding the flow of a recursive function:

递归函数涉及递归调用和基本情况 。 递归调用是函数主体的一部分，它会自行调用直到满足指定条件为止，而基本情况是函数的停止点。 有一个基本案例很重要，因为没有它，我们将陷入无限循环。 下面的教育图有助于理解递归函数的流程：

Educative 教育

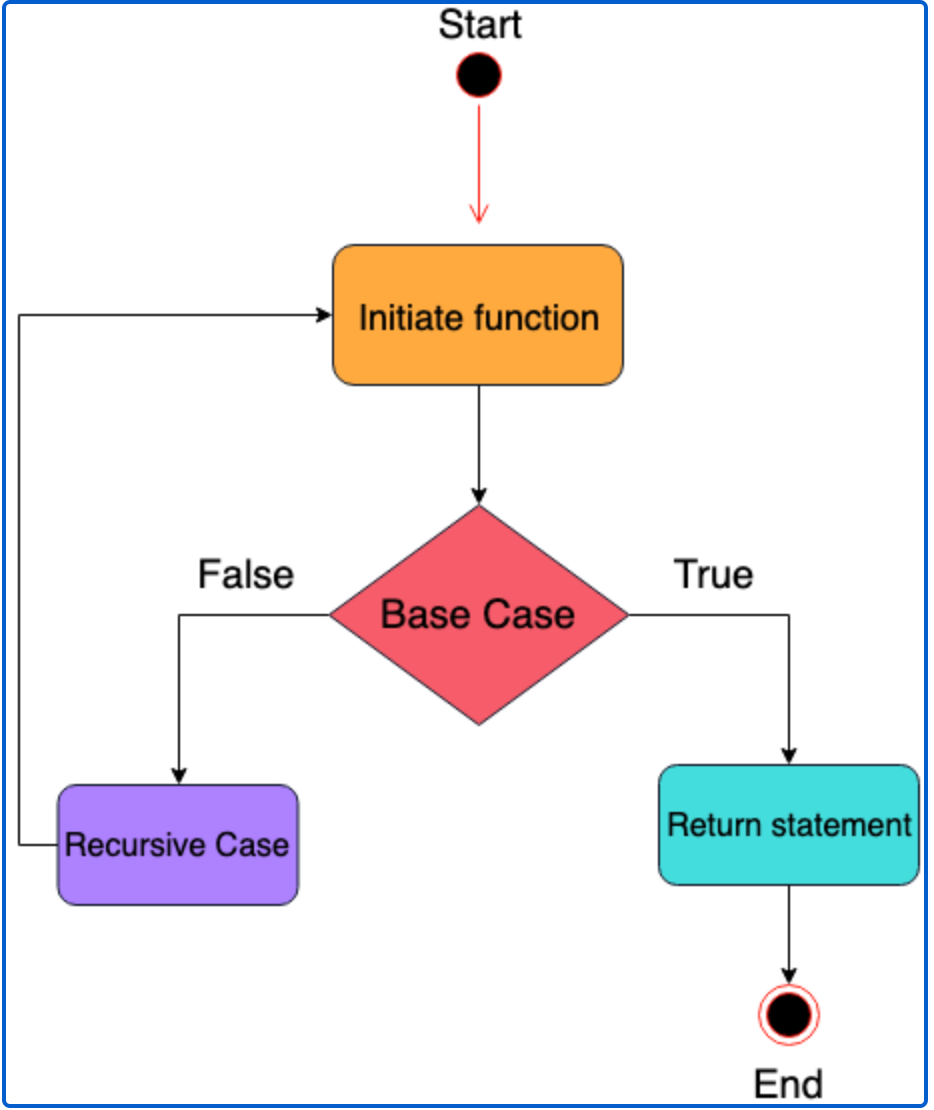
Let’s take a look at an example of a recursive function to illustrate the concept:

让我们看一个递归函数的例子来说明这个概念：

function printString(myString) {
   console.log(myString[0]);   if (myString.length > 1) {
      let mySubString = myString.substring(1, myString.length);           
      printString(mySubString); // recursive call
   } else {
      return true; // base case
   }
}

In the above example, we are using recursion to print out each character of a string by first printing out the first character of the string. If the string is more than one character long, we then take a substring of the original string and make a recursive call, repeating this process until the length of our string is only one character — this is our base case, upon which we will exit the recursive function.

在上面的示例中，我们使用递归通过首先打印出字符串的第一个字符来打印出字符串的每个字符。 如果字符串的长度超过一个字符，则我们将原始字符串的一个子字符串作为一个字符串进行递归调用，重复此过程，直到字符串的长度仅是一个字符为止—这是我们的基本情况，在此情况下，我们将退出递归函数。

In a JavaScript recursive function, the function is repeatedly called until it hits the base case. Only when the base case is reached and provides a solution can the recursive calls be evaluated.

在JavaScript递归函数中，该函数会反复调用，直到遇到基本情况为止。 仅当达到基本情况并提供解决方案时，才能评估递归调用。

Why do we care about recursion? While recursion is not an appropriate method for every case, it is an important concept to understand. Programming involves recursive thinking, and it can help us to write shorter and more efficient code when used appropriately.

我们为什么要关心递归？ 尽管递归并不是在每种情况下都适用的方法，但它是一个重要的概念。 编程涉及递归思维，当适当使用时，它可以帮助我们编写更短，更高效的代码。

While iterative functions can usually do the same job, recursive functions are simpler to read and understand. Recursive functions are especially powerful in traversing tree structures. Another reason that recursion is important to understand is that many algorithms use recursion. One downside to recursive functions, however, is that they usually require more memory space and tend to be slower than iterative functions.

尽管迭代函数通常可以完成相同的工作，但递归函数更易于阅读和理解。 递归函数在遍历树结构时特别强大。 理解递归很重要的另一个原因是许多算法都使用递归。 但是，递归函数的一个缺点是它们通常需要更多的存储空间，并且比迭代函数要慢。

freeCodeCamp freeCodeCamp

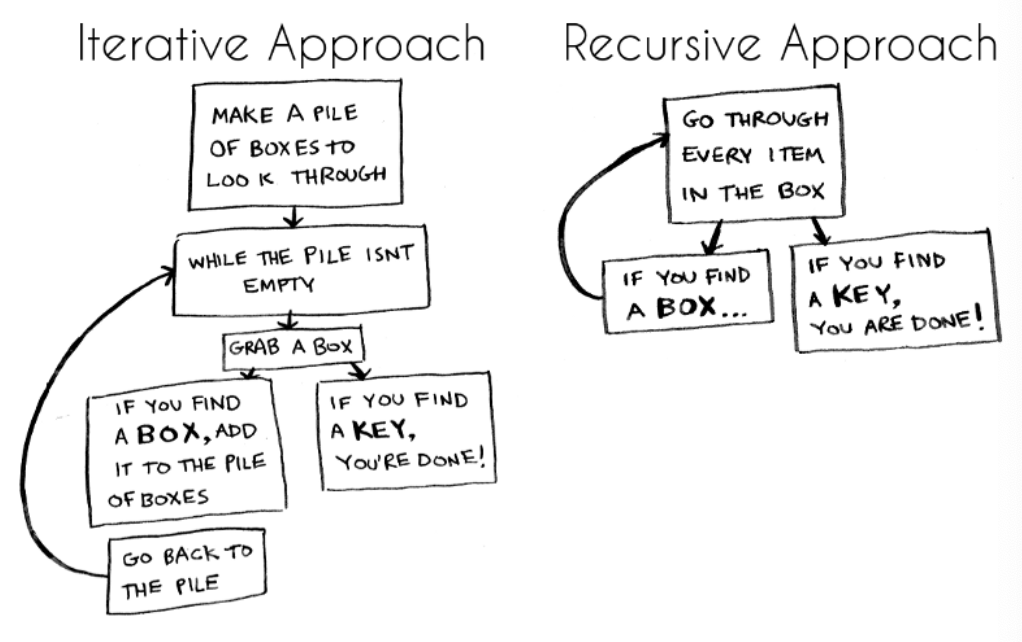
Strings and arrays are two data structures that especially lend themselves to recursive solutions. We can think of strings as data structures that are composed of smaller, overlapping substrings. Similarly, we can think of the properties of an array as a series of sub-arrays.

字符串和数组是两个数据结构，尤其适合于递归解决方案。 我们可以将字符串视为由较小的重叠子字符串组成的数据结构。 同样，我们可以将数组的属性视为一系列子数组。

A good way of finding a recursive solution to a problem is to apply the following steps:

查找问题的递归解决方案的一种好方法是应用以下步骤：

1. Choose a specific example to illustrate the concept of the problem.

1.选择一个特定的示例来说明问题的概念。

2. Come up with a function that provides a solution to the specific example.

2.提出一个为特定示例提供解决方案的功能。

3. Reframe the solution so that recursion is applied. Reword the function so that it invokes itself within the function body.

3.重新构造解决方案，以便应用递归。 重命名该函数，以便它在函数体内调用自身。

While the concept of a recursive function can initially be difficult to grasp, the more we practice it, the clearer it becomes.

虽然最初很难理解递归函数的概念，但是我们实践的越多，它就会变得越清晰。

翻译自: https://medium.com/better-programming/recursive-functions-2b5ce4610c81

递归函数问题