袋装决策树_袋装树是每个数据科学家需要的机器学习算法

袋装决策树

袋装树木介绍 (Introduction to Bagged Trees)

Without diving into the specifics just yet, it’s important that you have some foundation understanding of decision trees.

尚未深入研究细节，对决策树有一定基础了解就很重要。

From the evaluation approach of each algorithm to the algorithms themselves, there are many similarities.

从每种算法的评估方法到算法本身，都有很多相似之处。

If you aren’t already familiar with decision trees I’d recommend a quick refresher here.

如果您还不熟悉决策树，我建议在这里快速复习。

With that said, get ready to become a bagged tree expert! Bagged trees are famous for improving the predictive capability of a single decision tree and an incredibly useful algorithm for your machine learning tool belt.

话虽如此，准备成为袋装树专家！ 袋装树以提高单个决策树的预测能力和对您的机器学习工具带非常有用的算法而闻名。

什么是袋装树？什么使它们如此有效？ (What are Bagged Trees & What Makes Them So Effective?)

为什么要使用袋装树木 (Why use bagged trees)

The main idea between bagged trees is that rather than depending on a single decision tree, you are depending on many many decision trees, which allows you to leverage the insight of many models.

套袋树之间的主要思想是，您不依赖于单个决策树，而是依赖于许多决策树，这使您可以利用许多模型的洞察力。

偏差偏差的权衡 (Bias-variance trade-off)

When considering the performance of a model, we often consider what’s known as the bias-variance trade-off of our output. Variance has to do with how our model handles small errors and how much that potentially throws off our model and bias results in under-fitting. The model effectively makes incorrect assumptions around the relationships between variables.

在考虑模型的性能时，我们经常考虑所谓的输出偏差-偏差权衡。 方差与我们的模型如何处理小错误以及与模型的潜在偏离和导致拟合不足的偏差有关。 该模型有效地围绕变量之间的关系做出了错误的假设。

You could say the issue with variation is while your model may be directionally correct, it’s not very accurate, while if your model is very biased, while there could be low variation; it could be directionally incorrect entirely.

您可以说变化的问题在于，模型可能在方向上是正确的，但不是很准确；而如果模型有很大偏差，那么变化可能就很小。 它可能完全是方向错误的。

The biggest issue with a decision tree, in general, is that they have high variance. The issue this presents is that any minor change to the data can result in major changes to the model and future predictions.

通常，决策树的最大问题是它们的差异很大。 这带来的问题是，数据的任何细微变化都可能导致模型和未来预测的重大变化。

The reason this comes into play here is that one of the benefits of bagged trees, is it helps minimize variation while holding bias consistent.

之所以在这里发挥作用，是因为袋装树木的好处之一是，它可以在保持偏差一致的同时最大程度地减少变化。

为什么不使用袋装树木 (Why not use bagged trees)

One of the main issues with bagged trees is that they are incredibly difficult to interpret. In the decision trees lesson, we learned that a major benefit of decision trees is that they were considerably easier to interpret. Bagged trees prove the opposite in this regard as its process lends to complexity. I’ll explain that more in-depth shortly.

套袋树的主要问题之一是难以解释。 在决策树课程中，我们了解到决策树的主要好处是它们易于解释。 袋装树在这方面被证明是相反的，因为其过程增加了复杂性。 我将在短期内更深入地解释。

什么是装袋？ (What is bagging?)

Bagging stands for Bootstrap Aggregation; it is what is known as an ensemble method — which is effectively an approach to layering different models, data, algorithms, and so forth.

Bagging代表Bootstrap聚合； 这就是所谓的集成方法，实际上是一种对不同模型，数据，算法等进行分层的方法。

So now you might be thinking… ok cool, so what is bootstrap aggregation…

所以现在您可能在想……好极了，那么引导聚合是什么……

What happens is that the model will sample a subset of the data and will train a decision tree; no different from a decision tree so far… but what then happens is that additional samples are taken (with replacement — meaning that the same data can be included multiple times), new models are trained, and then the predictions are averaged. A bagged tree could include 5 trees, 50 trees, 100 trees and so on. Each tree in your ensemble may have different features, terminal node counts, data, etc.

发生的事情是该模型将对数据的一个子集进行采样并训练决策树。 到目前为止，它与决策树没有什么不同……但是接下来发生的是，将额外取样(进行替换-意味着可以多次包含相同的数据)，训练新模型，然后对预测取平均。 袋装树可以包括5棵树，50棵树，100棵树等等。 集合中的每棵树可能具有不同的功能，终端节点数，数据等。

As you can imagine, a bagged tree is very difficult to interpret.

可以想象，袋装树很难解释。

训练袋装树 (Train a Bagged Tree)

To start off, we’ll break out our training and test sets. I’m not going to talk much about the train test split here. We’ll be doing this with the Titanic dataset from the titanic package

首先，我们将介绍我们的培训和测试集。 在这里，我不会谈论太多有关火车测试的内容。 我们将使用titanic包中的Titanic数据集进行此操作

n <- nrow(titanic_train)n_train <- round(0.8 * n)set.seed(123) 
train_indices <- sample(1:n, n_train) 
train <- titanic_train[train_indices, ] 
test <- titanic_train[-train_indices, ]

Now that we have our train & test sets broken out, let’s load up the ipred package. This will allow us to run the bagging function.

现在我们有了训练和测试集，现在让我们加载ipred包。 这将使我们能够运行装袋功能。

A couple things to keep in mind is that the formula indicates that we want to understand Survived by (~ ) Pclass + Sex + Age + SibSp + Parch + Fare + Embarked

几件事情要记住的是，该公式表明我们想了解Survived的( ~ ) Pclass + Sex + Age + SibSp + Parch + Fare + Embarked

From there you can see that we’re using the train dataset to train this model. & finally, you can see this parameter coob. This is confirming whether we'd like to test performance on an out of bag sample.

从那里您可以看到我们正在使用训练数据集来训练此模型。 最后，您可以看到此参数coob 。 这证实了我们是否要测试袋装样品的性能。

Remember how I said that each tree re-samples the data? Well, that process leaves a handful of records that will never be used to train with & make up an excellent dataset for testing the model’s performance. This process happens within the bagging function, as you'll see when we print the model.

还记得我说过每棵树重新采样数据吗？ 好的，该过程留下了很少的记录，这些记录将永远不会用于训练并构成用于测试模型性能的出色数据集。 如我们在打印模型时所见，此过程在bagging功能内进行。

library(ipred) 
set.seed(123) 
model <- bagging(formula = Survived ~ Pclass + Sex + Age + SibSp + Parch + Fare + Embarked, data = train, coob = TRUE) 
print(model)

As you can see we trained the default of 25 trees in our bagged tree model.

如您所见，我们在袋装树模型中训练了25棵树的默认值。

We use the same process to predict for our test set as we use for decision trees.

我们使用与决策树相同的过程来预测测试集。

pred <- predict(object = model, newdata = test, type = "class") print(pred)

绩效评估 (Performance Evaluation)

Now, we’ve trained our model, predicted for our test set, now it’s time to break down different methods of performance evaluation.

现在，我们已经对模型进行了训练，并针对测试集进行了预测，现在是时候分解不同的性能评估方法了。

ROC曲线和AUC (ROC Curve & AUC)

ROC Curve or Receiver Operating Characteristic Curve is a method for visualizing the capability of a binary classification model to diagnose or predict correctly. The ROC Curve plots the true positive rate against the false positive rate at various thresholds.

ROC曲线或接收器工作特性曲线是一种可视化二进制分类模型正确诊断或预测的功能的方法。 ROC曲线在各种阈值下绘制了真实的阳性率相对于假阳性率。

Our target for the ROC Curve is that the true positive rate is 100% and the false positive rate is 0%. That curve would fall in the top left corner of the plot.

ROC曲线的目标是真实的阳性率为100％，错误的阳性率为0％。 该曲线将落在图的左上角。

AUC is intended to determine the degree of separability, or the ability to correct predict class. The higher the AUC the better. 1 would be perfect, and .5 would be random.

AUC旨在确定可分离性的程度或纠正预测类别的能力。 AUC越高越好。 1将是完美的，而.5将是随机的。

We’ll be using the metrics package to calculate the AUC for our dataset.

我们将使用metrics包来计算数据集的AUC。

library(Metrics) 
pred <- predict(object = model, newdata = test, type = "prob") auc(actual = test$Survived, predicted = pred[,"yes"])

Here you can see that I change the type to "prob" to return a percentage likelihood rather than the classification. This is needed to calculate AUC.

在这里，您可以看到我将type更改为"prob"以返回百分比可能性而不是分类。 这是计算AUC所必需的。

This returned an AUC of .89 which is not bad at all.

这返回的AUC为0.89，这还算不错。

截止阈值 (Cut-off Threshold)

In classification, the idea of a cutoff threshold means that given a certain percent likelihood for a given outcome you would classify it accordingly. Wow was that a mouthful. In other words, if you predict survival at 99%, then you’d probably classify it as survival. Well, let’s say you look at another passenger that you predict to survive with a 60% likelihood. Well, they’re still more likely to survive than not, so you probably classify them as survive. When selecting type = "pred" you have the flexibility to specify your own cutoff threshold.

在分类中，阈值阈值的概念意味着给定结果的百分比可能性一定，您就可以对其进行分类。 哇，真是满嘴。 换句话说，如果您预测生存率为99％，则可能会将其归类为生存。 好吧，假设您看另一名您预计会以60％的可能性幸存的乘客。 好吧，它们仍然更有可能生存，因此您可能将它们归类为生存。 选择type = "pred"您可以灵活地指定自己的截止阈值。

准确性 (Accuracy)

This metric is very simple, what percentage of your predictions were correct. The confusion matrix function from caret includes this.

这个指标非常简单，您的预测百分比正确无误。 caret的混淆矩阵函数包括此函数。

混淆矩阵 (Confusion Matrix)

The confusionMatrix function from the caret package is incredibly useful. For assessing classification model performance. Load up the package, and pass it your predictions & the actuals.

caret包中的confusionMatrix函数非常有用。 用于评估分类模型的性能。 加载程序包，并通过它您的预测和实际情况。

library(caret) 
confusionMatrix(data = test$pred, reference = test$Survived)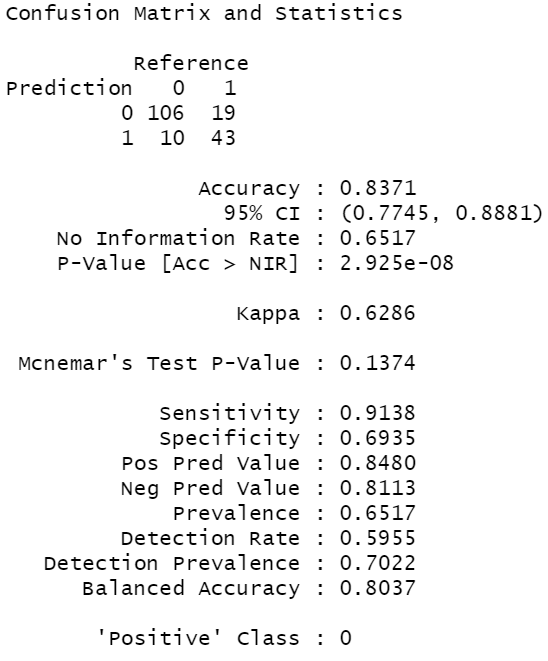

The first thing this function shows you is what’s called a confusion matrix. This shows you a table of how predictions and actuals lined up. So the diagonal cells where the prediction and reference are the same represents what we got correct. Counting those up 149 (106 + 43) and dividing it by the total number of records, 178; we arrive at our accuracy number of 83.4%.

此功能向您显示的第一件事是所谓的混淆矩阵。 这向您显示了有关预测和实际值如何排列的表格。 因此，预测和参考相同的对角线单元代表我们得到了正确的结果。 数出149(106 + 43)，然后除以记录总数178； 我们得出的准确率为83.4％。

True positive: The cell in the quadrant where both the reference and the prediction are 1. This indicates that you predicted survival and they did in fact survive.

真阳性：参考值和预测值均为1的象限中的单元格。这表示您预测了存活率，而实际上它们确实存活了。

False positive: Here you predicted positive, but you were wrong.

误报：您在这里预测为积极，但您错了。

True negative: When you predict negative, and you are correct.

真正的负面：当您预测为负面时，您是正确的。

False negative: When you predict negative, and you are incorrect.

假阴性：当您预测为阴性时，您是不正确的。

A couple more key metrics to keep in mind are sensitivity and specificity. Sensitivity is the percentage of true records that you predicted correctly.

还有两个要记住的关键指标是敏感性和特异性。 灵敏度是您正确预测的真实记录的百分比。

Specificity, on the other hand, is to measure what portion of the actual false records you predicted correctly.

另一方面，特异性是衡量您正确预测的实际错误记录的哪一部分。

Specificity is one to keep in mind when predicting on an imbalanced dataset. A very common example of this is for classifying email spam. 99% of the time it’s not spam, so if you predicted nothing was ever spam you’d have 99% accuracy, but your specificity would be 0, leading to all spam being accepted.

在不平衡数据集上进行预测时，应牢记特异性。 一个非常常见的示例是对电子邮件垃圾邮件进行分类。 99％的时间不是垃圾邮件，因此，如果您预测没有东西是垃圾邮件，则您将具有99％的准确性，但是您的特异性将是0，从而导致所有垃圾邮件都被接受。

结论 (Conclusion)

In summary, we’ve learned about the right times to use bagged trees, as well as the wrong times to use them.

总而言之，我们已经了解了使用袋装树的正确时间以及使用袋树的错误时间。

We defined what bagging is and how it changes the model.

我们定义了什么是装袋以及它如何改变模型。

We built and tested our own model while defining & assessing a variety of performance measures.

我们在定义和评估各种绩效指标的同时建立并测试了自己的模型。

I hope you enjoyed this quick lesson on bagged trees. Let me know if there was something you wanted more info on or if there’s something you’d like me to cover in a different post.

我希望您喜欢这个关于袋装树木的快速课程。 让我知道您是否想了解更多信息，或者是否希望我在其他帖子中介绍。

Happy Data Science-ing!

快乐数据科学！

翻译自: https://towardsdatascience.com/bagged-trees-a-machine-learning-algorithm-every-data-scientist-needs-d8417ec2e0d9

袋装决策树