使用蒙特卡洛模拟进行var计算

财务和投资组合风险管理中的VaR？ (VaR in Financial and Portfolio Risk Management?)

VaR is an acronym of ‘Value at Risk’, and is a tool which is used by many firms and banks to establish the level of financial risk within its firm. The VaR is calculated for an investments of a company’s investments or perhaps for checking the riks levels of a portfolio managed by the wealth management branch of a bank or a boutique firm.

VaR是“风险价值”的缩写，是许多公司和银行用来确定公司内部金融风险水平的工具。 VaR的计算是针对公司投资的投资，或者是为了检查由银行或精品公司的财富管理分支机构管理的投资组合的风险水平。

The calculation may be thought of as a statistical measure in isolation. It can also be simplified to the following example statement -

可以将该计算孤立地视为统计量度。 也可以将其简化为以下示例语句-

VaR is the minimum loss which will be incurred at a certain level of probability (confidence interval) OR the maximum loss which will be realized at a level of probability.

VaR是在一定概率水平(置信区间)下发生的最小损失，或在概率水平下实现的最大损失。

Photo Credit — SP Consulting LLP

照片信用— SP Consulting LLP

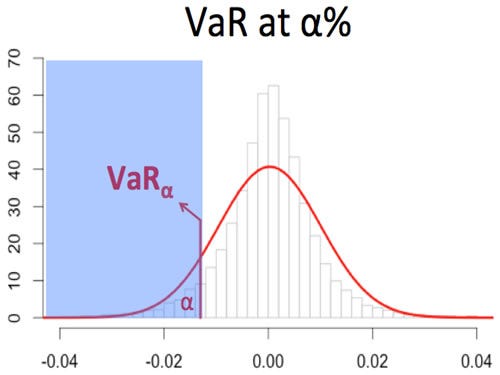
The above image shows the maximum loss which can be faced by a company at a α% confidence. On a personal level VaR can help you predict or analyse the maximum losses which your portfolio is likely to face — this is something which we will analyse soon.

上图显示了公司在α ％置信度下可能面临的最大损失。 从个人角度而言，VaR可以帮助您预测或分析您的投资组合可能面临的最大损失-我们将尽快对此进行分析。

蒙特卡洛模拟 (Monte Carlo Simulations)

The Monte Carlo model was the brainchild of Stanislaw Ulam and John Neumann, who developed the model after the second world war. The model is named after a gambling city in Monaco, due to the chance and random encounters faced in gambling.

蒙特卡洛模型是斯坦尼斯拉夫·乌兰(Stanislaw Ulam)和约翰·诺伊曼(John Neumann)的创意，他们在第二次世界大战后开发了该模型。 该模型因在摩纳哥的一个赌博城市而得名，这是由于赌博中的机会和随机遭遇。

The Monte Carlo simulation is a probability model which generates random variables used in tandem with economic factors (expected return, volatility — in the case of a portfolio of funds) to predict outcomes over a large spectrum. While not the most accurate, the model is often used to calculate the risk and uncertainty.

蒙特卡洛模拟是一个概率模型，该模型生成与经济因素(预期收益，波动率—在基金组合的情况下)串联使用的随机变量，以预测大范围的结果。 虽然不是最准确，但该模型通常用于计算风险和不确定性。