算法-MANACHAR 求最长回文串 JAVA版本_用java计算回文串-优快云博客

本文深入探讨了Manachar算法，一种高效的回文串查找方法。该算法通过在字符串中插入特殊字符并利用回文串的对称性质，能够在O(n)的时间复杂度内找出最长的回文子串。文章详细解释了算法的实现步骤，并提供了优化后的代码示例。

一、背景

Manachar主要是为了处理回文串问题，回文串的定义不再赘述。一般来讲，判定一个字符串中的子串是否是回文串，常规的方法是遍历字符串的每一个字符，然后向左右扩展，这样可以判定是否是回文串、回文串的长度，以及字符串中最长的回文子串是什么。这样的方法比较暴力，算法复杂度是O(n2)，实际使用上是比较慢了。1975年，Manachar发明了Manachar算法，能以的算法复杂度O(n)来处理这个问题。速度还是比较快的。
原文链接：https://blog.youkuaiyun.com/iwts_24/article/details/82430393

二、算法套路

首先直接在字符串间加#

第二步，分以下四种可能性：

1）暴力扩最右回文半径

2） a. 索引下标i对应的回文半径在最右回文半径以内，直接取回文中心对称点i’，O（1）

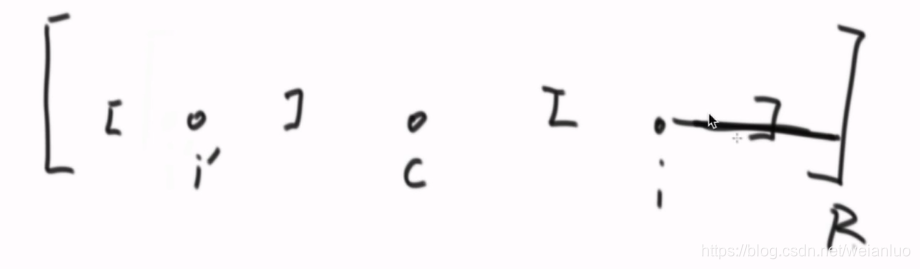
PS: C为取得最右边界时候的回文中心

b.索引下标i对应的回文半径在最右回文半径外，取i到R的距离，O（1）

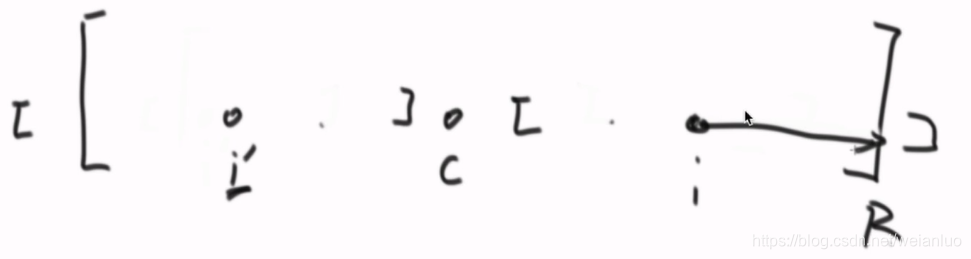
PS:情况a和b用一段代码表示：pArr[i] = pR > i ? Math.min(pArr[2 * C- i], pR - i) : 1; 2 * C- i求得为i'

c.索引下标i对应的回文半径刚好在最右回文半径上，暴力扩

三、代码

代码做了优化，本来情况a和b不需要暴力扩的，但放在暴力扩里面了，因为他们一扩就失败，直接break，为了代码更短。

	public static char[] manacherString(String str) {
		char[] charArr = str.toCharArray();
		char[] res = new char[str.length() * 2 + 1];
		int index = 0;
		for (int i = 0; i != res.length; i++) {
			res[i] = (i & 1) == 0 ? '#' : charArr[index++];
		}
		return res;
	}

	public static int maxLcpsLength(String str) {
		if (str == null || str.length() == 0) {
			return 0;
		}
		char[] charArr = manacherString(str);
		int[] pArr = new int[charArr.length];
		int index = -1;
		int pR = -1;
		int max = Integer.MIN_VALUE;
		for (int i = 0; i != charArr.length; i++) {
			pArr[i] = pR > i ? Math.min(pArr[2 * index - i], pR - i) : 1;
			while (i + pArr[i] < charArr.length && i - pArr[i] > -1) {
				if (charArr[i + pArr[i]] == charArr[i - pArr[i]])
					pArr[i]++;
				else {
					break;
				}
			}
			if (i + pArr[i] > pR) {
				pR = i + pArr[i];
				index = i;
			}
			max = Math.max(max, pArr[i]);
		}
		return max - 1;
	}

	public static void main(String[] args) {
		String str1 = "abc1234321ab";
		System.out.println(maxLcpsLength(str1));
	}