【算法】二分查找

原创已于 2025-08-24 19:59:43 修改 · 937 阅读

11 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #数据结构

于 2025-08-24 19:59:20 首次发布

算法专栏收录该内容

7 篇文章

订阅专栏

1、算法原理

在序列中查找目标值（target）时，若序列具有"二段性"特征（即能被划分为两个满足不同性质的子序列），则可以通过判断中间值所属的性质，直接排除其中一半的序列元素。再判断没有被排除的序列中间值所属的性质，再直接排除其中一半的序列元素，直到只剩下一个序列元素，则这个序列元素可能是目标值。

2、时间复杂度

每次都排除一半的序列元素，直到只剩下一个序列元素。假设序列有 n 个元素，每次判断后剩下的元素个数：

n/2 ----> n/(2^2) ----> n/(2^3) ----> n/(2^4) ----> n/(2^5) ----> n/(2^6) ----> ... ----> n/(2^N) = 1

则 N = logn，N 就是查找的次数，所以时间复杂度是 logn

求序列的中间值索引的方式：

1、mid = left + (right - left) / 2;

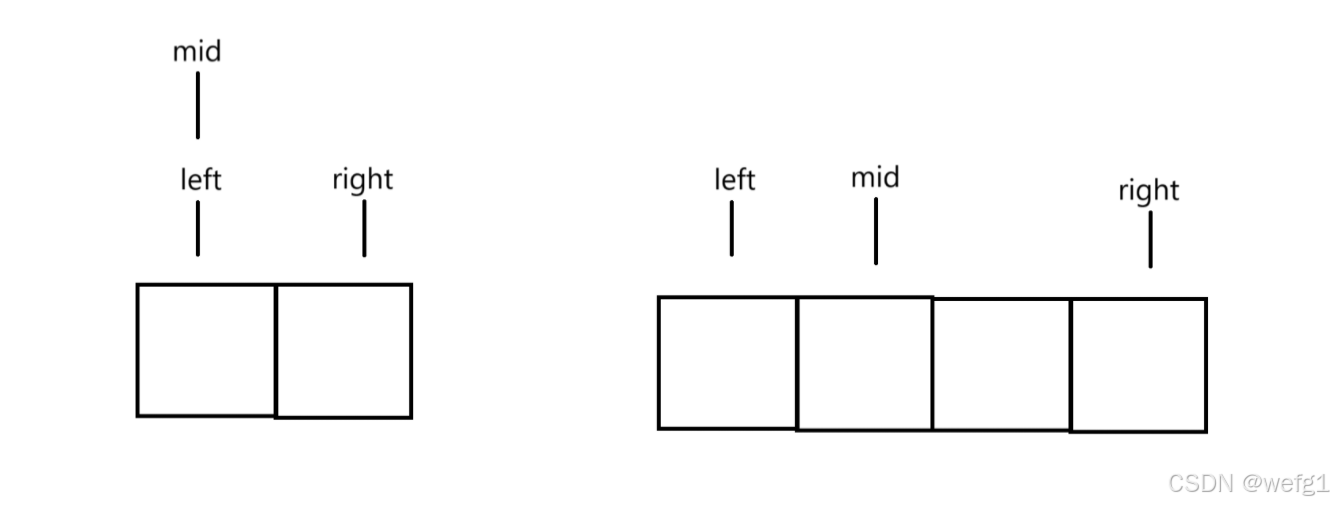
2、mid = left + (right - left + 1) / 2;

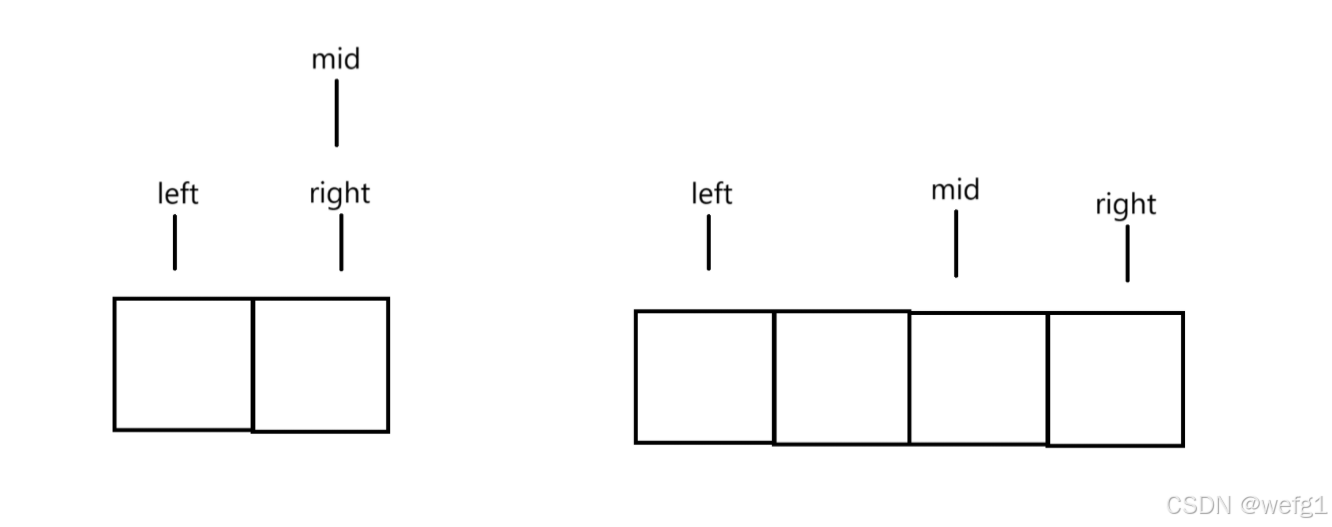
这两种方式在标准二分查找模板都可以，但在常用二分查找模板有区别。不推荐 mid = (left + right) / 2，这种方式，如果序列太长容易溢出。

2、标准二分查找模板

在一段序列中查找目标值

int left = 0,right = nums.size() - 1;

while(left <= right) // 注意循环继续的条件
{
    int mid = left + (right - left) / 2; // 如果序列太长，防止溢出
    if(...) right = mid - 1;
    else if(...) left = mid + 1;
    else return ...;
}

return ...;
// 说明：... 是根据题目所推导的二段性

例题：

class Solution {
public:
    int search(vector<int>& nums, int target) {
    int left = 0,right = nums.size() - 1;

    while(left <= right)
    {
        int mid = left + (right - left) / 2;
        if(nums[mid] > target) right = mid - 1;
        else if(nums[mid] < target) left = mid + 1;
        else return mid;
    }

    return -1;
    }
};

3、常用二分查找模板

将序列分为左右两个序列，左右两个序列的元素都满足某个特点，而要查找的元素通常是左序列的右端点或者是右序列的左端点。

如果要查找的目标值是右序列的左端点：

while (left < right)
{
    int mid = left + (right - left) / 2；

    if (mid 所指向的元素满足右序列的特点) right = mid; 
    else if (mid 所指向的元素满足左序列的特点) left = mid + 1;
}

注意：

1、注意求序列中间值的方式，不能写成 int mid = left + (right - left + 1) / 2; 否则会死循环

2、不能是 right = mid - 1; 因为 mid 所在位置可能就是目标值

如果要查找的目标值是左序列的右端点：

while (left < right)
{
    int mid = left + (right - left + 1) / 2；

    if (mid 所指向的元素满足右序列的特点) right = mid - 1; 
    else if (mid 所指向的元素满足右序列的特点) left = mid;
}

注意：

1、注意求序列中间值的方式，不能写成 int mid = left + (right - left) / 2; 否则会死循环

2、不能是 left = mid - 1; 因为 mid 所在位置可能就是目标值

例题：

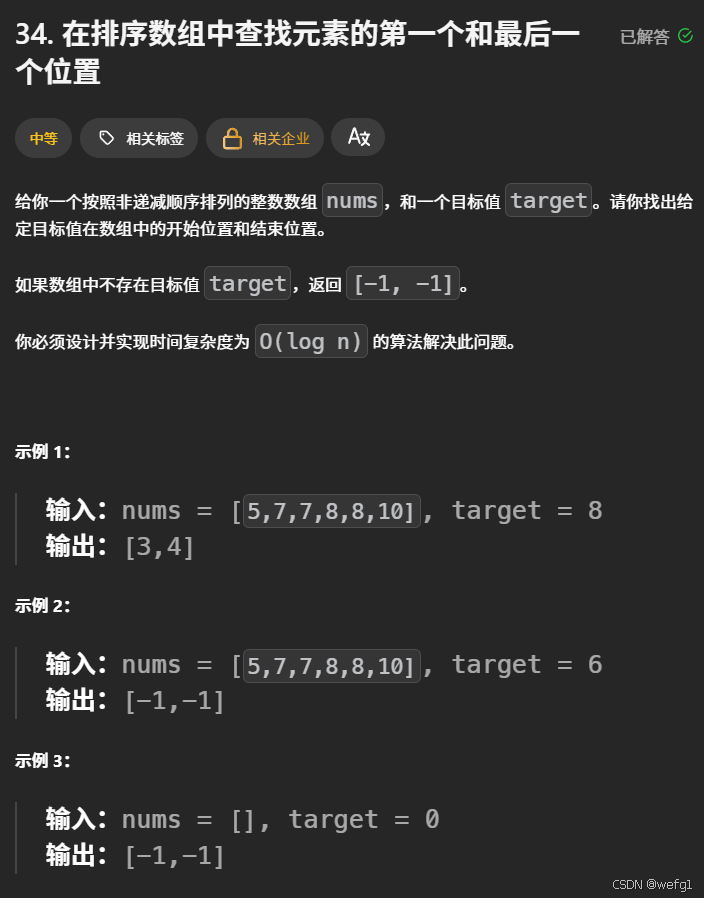
二段性分析：以求左端点为例，这道题的二段性可以是将序列分为两个子序列，左序列都是小于 target 的值，而右序列都是大于等于 target 的值。

class Solution {
public:
    vector<int> searchRange(vector<int>& nums, int target) {
        vector<int> ret = {-1,-1};
        int left = 0;
        int right = nums.size() - 1;
        
        if(nums.size() == 0) return ret; //处理边界情况

        // 寻找左端点
        while(left < right)
        {
            int mid = left + (right - left) / 2;
            if(nums[mid] < target) left = mid + 1;
            if(nums[mid] >= target) right = mid;
        }

        if(nums[left] == target) ret[0] = left;
        else return ret;

        // 寻找右端点
        left = 0;
        right = nums.size() - 1;

        while(left < right)
        {
            int mid = left + (right - left + 1) / 2;
            if(nums[mid] <= target) left = mid;
            if(nums[mid] > target) right = mid - 1;
        }

        if(nums[right] == target) ret[1] = right;
        else return ret;

        return ret;
    }
};

二段性分析：这道题的二段性可以是左序列都是平方后小于等于 target 的值，而右序列都是平方后大于 target 的值。

class Solution {
public:
    int mySqrt(int x) {
    
        int left = 0,right = x;
        long long mid = 0; // 防止溢出
        while(left < right)
        {
            mid = left + (right - left + 1) / 2;
        
            if(mid * mid > x) right = mid - 1;
            else if(mid * mid < x) left = mid;
            else if(mid * mid == x) return mid;
        }
        
        return left;
    }
};

二段性分析：这道题的二段性可以是将序列分为两个子序列，左序列都是小于 target 的值，而右序列都是大于等于 target 的值。最后 left 和 right 相遇指向的值时有两种情况：1、该值大于等于 target，此时直接返回 left 或 right，2、该值小于 target，因为序列的值可能都是小于 target 的值，此时返回 left + 1 或 right + 1。

int left = 0, right = nums.size() - 1;
while (left < right)
{
    int mid = left + (right - left) / 2;

    if (nums[mid] >= target) right = mid;
    else if (nums[mid] < target) left = mid + 1;
}

if (nums[left] < target) return left + 1;
else return left;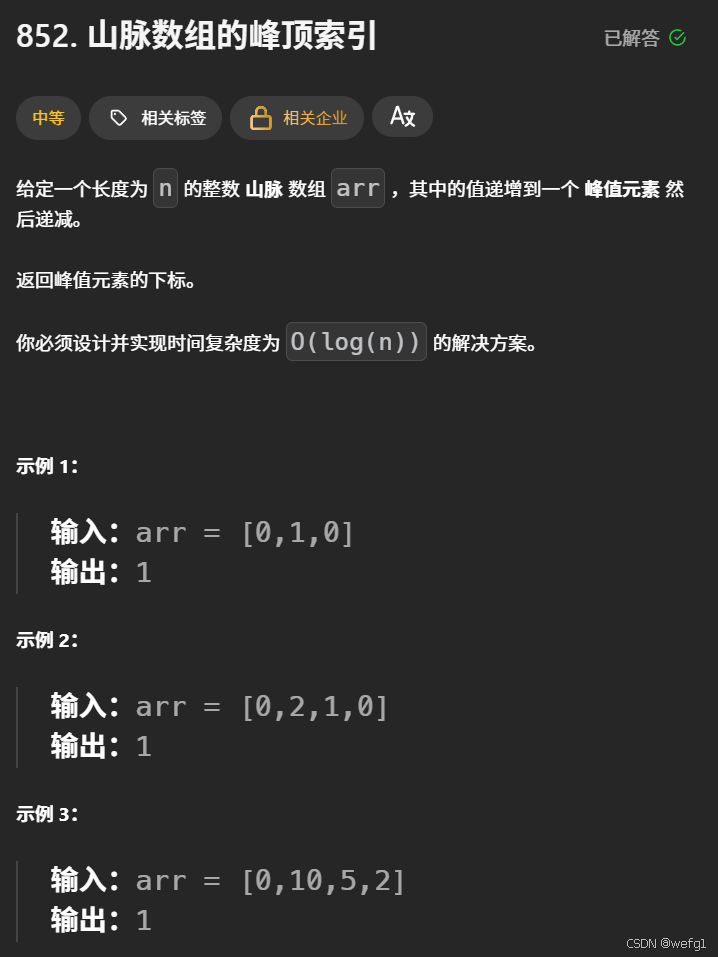

二段性分析：数组可以分为左右两个子序列，左序列是包含峰顶在内的递增序列，右序列是递减序列。左序列元素的特点是从下标为 1 的元素开始，每个元素都大于它前一个元素，右序列元素的特点是每个元素都小于它前一个元素。

class Solution {
public:
    int peakIndexInMountainArray(vector<int>& arr) {
       
        // 数组首元素和最后一个元素不可能是峰顶
        int left = 1,right = arr.size() - 2; 
        while(left < right)
        {
            int mid = left + (right - left + 1) / 2;
            if(arr[mid] > arr[mid - 1]) left = mid;
            else right = mid - 1;
        }

        return left;
    }
};

二段性分析：关键是某一时刻选取到的 mid 指向的元素，通过该元素与它下一个元素做比较，如果 mid 大于它下一个元素，那么峰值可能是 mid 或可能是包含在 mid 左边的某个元素，如果 mid 小于它下一个元素，那么峰值可能是包含在 mid 右边的某个元素。

class Solution {
public:
    int findPeakElement(vector<int>& nums) {
        int left = 0,right = nums.size() - 1;

        while(left < right)
        {
            int mid = left + (right - left) / 2;

            if(nums[mid] > nums[mid + 1]) right = mid;
            else if(nums[mid] < nums[mid + 1]) left = mid + 1;
        }

        return left;
    }
};

二段性分析：根据题目，由于序列的元素互不相同，我们把序列抽象成折线图：

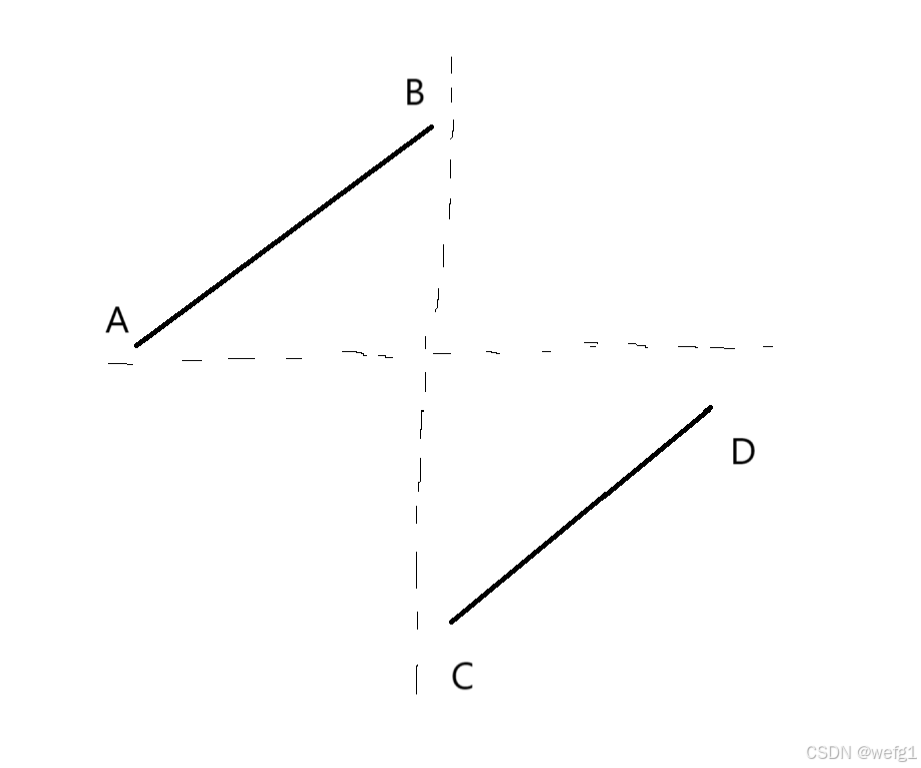
如果 mid 落在 AB 段，那么 mid指向的元素一定大于 D 点（序列最后一个元素），此时应该到右序列寻找，left = mid + 1；如果 mid 落在 CD 段，那么 mid 指向的元素一定小于等于 D 点，此时应该到序列左端点寻找，right = mid（mid 可能落在 C 点，所以不能是 right = mid - 1）。

class Solution {
public:
    int findMin(vector<int>& nums) {
       int left = 0,right = nums.size() - 1;
       int flag = nums[right];

       while(left < right)
       {
            int mid = left + (right - left) / 2;

            if(nums[mid] > flag) left = mid + 1;
            else right = mid;
       }

       return nums[left];
    }
};

这道题可以一题多解：1、哈希表 2、暴力解法 3、位运算 4、求和公式 5、二分查找。

二段性分析：在缺失某个数字之前的数字，该数字与它的下标一一对应，缺失的哪个数字及以后，下标不对应。根据该性质可以将序列分为两个子序列：下标对应的序列与下标不对应的序列。

class Solution {
public:
    int takeAttendance(vector<int>& records) {
        int left = 0,right = records.size() - 1;
        
        while(left < right)
        {
            int mid = left + (right - left) / 2;

            if(mid == records[mid]) left = mid + 1;
            else right = mid;
        }

        if(left == records[left]) return left + 1;
        else return left;
    }
};