基于RTS盒与相位嵌入的图像加密

一种基于多个右移高级加密标准格雷S盒与相位嵌入的新型模糊加密技术

引言

由于不同图像文件通过互联网[1, 2]的广泛传输，数字图像的安全需求日益增加。因此，开发一些算法来保护秘密图像至关重要。研究人员提出了多种类型的图像安全技术。密码学和隐写术是两种广泛使用的技术，用于保护秘密图像的内容。密码学的基本原理是通过在其信息中引入混淆，将秘密图像（明文图像）转换为扩散后的图像（密文图像）。在许多密码系统中，替换盒（S盒）是图像中实现扩散的唯一关键组件。Daemen和 Rijmen提出了一种分组密码，该密码被美国国家标准与技术研究院采用为高级加密标准（AES）[4]。目前，高级加密标准是常用的密码系统。由于S盒在高级加密标准中的核心作用，许多密码学家已将其研究重点放在 AES S盒上。文献[5]中给出了rijndael分组密码的代数表达式。文献[6],中提出了一种新的、简单的AES S盒数学描述。

在[7]中提出了高级加密标准S盒的置换多项式表示。观察到高级加密标准S盒的多项式仅有九个非零项，这表明AES的安全性可能易受计算攻击的影响[6,7]。为了消除AES的这一弱点，许多研究人员已提出新的S盒（例如参见[8–13]）。在[8],中提出了一种改进的S盒。他们工作的缺点是其S盒无法利用现有的AES框架实现。AES S盒复杂度较低的原因在[9]中被识别出来。此外，在[9]中还提出了一种新版本的S盒。在[10],中，基于仿射映射开发了另一种S盒，其多项式包含253个非零项，并可重用现有的AES实现。在[11]中通过引入基于格雷码的S盒进一步增强了高级加密标准S盒的代数复杂度。改进后的S盒具有255个非零项，并重用了整个现有的AES框架。在[12]中提出了Gray S盒的推广。利用伽罗瓦域GF(2^8)的右移位和正则表示生成了256个不同的RTSs，均具有高代数复杂度，并满足非线性等其他安全测试要求。

在隐写术中，秘密图像被嵌入到另一幅称为宿主图像的图像中。这种嵌入方式使得未经授权的用户无法在结果图像[16–19]中检测到秘密图像的存在。近年来，许多科学家开发了基于密码学与隐写术相结合的新图像安全算法。在[20],中，提出了一种针对灰度图像的隐写密码系统，该系统采用光学加密、相位嵌入和固定数据隐藏技术。在[21],中，提出了一种采用自适应数据隐藏技术的改进型隐写密码系统。在[22]中，使用混沌S盒来提高将秘密图像嵌入宿主图像后的安全性。在[23],中，首先使用高级加密标准对秘密图像I进行加密，然后利用最低有效位（LSB）嵌入技术将其嵌入宿主图像中。类似地，许多其他研究人员也提出了各种隐写密码系统（例如，参见[24–27]）。

本文提出了一种基于可变多RTS盒和隐写术的新型图像安全系统。该技术使用四种不同的RTS盒和相位嵌入技术。采用模糊方法选择RTS盒，其选择取决于秘密图像的像素。所提出的算法还利用秘密图像的空间域和频率域以实现混淆目的。该技术的目标是构建一种安全系统，相较于单S盒安全技术和隐写密码系统，能够更有效地抵抗计算攻击。对所提出的密码系统进行了多项测试，以评估其安全强度。实验结果表明，与一些著名的现有安全算法相比，所提出的安全技术对计算攻击具有高抗性。本文其余部分组织如下：第2节介绍预备知识。第3节提出了新型加密技术。第4节包含分析与比较。最后，第5节给出结论和未来研究方向。

2. 预备知识

2.1. 模糊集

模糊集是一对(f,X)，其中X是一个集合，而f是从集合X到区间[0,1]的函数。该函数f称为隶属函数，用于表示元素在(f,X)中X的隶属度。如今，模糊理论已广泛应用于许多密码系统中（例如参见[28–30]）。

2.2 右移位高级加密标准格雷S盒（RTSs）

一种生成多个S盒的技术在[12]中被提出。该技术利用伽罗瓦域 GF(2^8)的正则表示和格雷码[31]。该技术的主要优点是能够生成代数结构复杂的S盒，对应于GF(2^8)中的每个元素。由于GF(2^8)中有256个元素，因此共有256个不同的RTSs。RTSs生成的数学表达式如下所示：

$$
\xi(g) = SAES \circ \rho_g \circ G,
$$

其中g是GF(2^8)中的元素c，SAES是AES S盒，ρg是g的置换表示，G是格雷码映射，ξ(g)是对应于g的RTS。

3. 提出的安全系统

在本节中，我们提出了一种基于RTSs和隐写术的新安全系统。设I为秘密图像，J为宿主图像。I和J均为尺寸相同的灰度图像M × N。下面给出所提出的加密和解密算法的主要步骤。

3.1. 加密算法

步骤1. S盒模糊选择准则：

(a) 定义一个模糊集(f, GF(2^8))，通过
$$
f(g) = \frac{#(g)}{M \times N},
$$
其中#(g)是g在I中的出现频率。该模糊集给出了伽罗瓦域GF(2^8)中每个元素在秘密图像中的隶属度。

(b) 假设l是f的值域的上确界；即，$ l = \sup{f(g)} $。

(c) 现在，计算l的原像g₁,g₂,g₃,…,gₙ。这些原像的下确界g是GF(2^8)中在秘密图像I中具有最大隶属度的最小元素。

(d) 将I与ξ(g)（对应于g的RTS）进行扩散，得到Ig。

步骤2. 在空间域和频率域中生成随机掩模并进行混淆：

(a) 固定GF(2^8)中的一个元素 c ，并通过使用(1)及以下三个方程选择三个RTSs ξ(S₁)、ξ(S₂) 和 ξ(S₃)：

$$
S_1 = g + c \pmod{256}, \
S_2 = S_1 + c \pmod{256}, \
S_3 = S_2 + c \pmod{256}.
$$

(b) 在宿主图像 J 上应用 ξ(S₁) 和 ξ(S₂)，以得到其两个不同的扩散版本 J₁ 和 J₂。

(c) 现在生成两个随机掩模 R₁ 和 R₂，用于在扩散后的密像 Ig 的空间域和频率域中产生混淆。这些掩模的数学表达式如下所示：

$$
R_1 = \exp\left(i \frac{\pi}{2} J_1^8\right), \
R_2 = \exp\left(i \frac{\pi}{2} J_2^8\right).
$$

然后通过使用在Ig的内容中生成随机噪声：

$$
I_R = F^{-1}[F(I_g \times R_1) \times R_2],
$$

其中 F 是傅里叶变换，F⁻¹ 是逆傅里叶变换。

步骤3. 宿主图像的安全与嵌入过程：
只有在已知R₁和R₂的情况下，解密过程才能完成。传统上，可以通过将R₁和R₂嵌入到IR中来获取它们。但这一过程会增加加密图像的大小，并影响解密图像的质量 [20–22]。尽管如此，我们仍将IR嵌入宿主图像中，因为R₁和R₂可以通过J重新生成。通过使用对应于S₃的RTS对J进行扩散，可使宿主图像免受第三方攻击，即ξ(S₃)。最后，将IR和g嵌入到扩散后的宿主图像 J₃的相位项中。以下是嵌入过程的数学方程：

$$
I_S = J_3 \exp\left(i \frac{\pi}{2} I_R\right).
$$

所提出的加密过程在图1(a)中进行了详细说明。

3.2. 解密算法

步骤1. 在解密过程中，首先通过计算IS的复模和辐角提取J₃、IR 和g：

$$
J_3 = |I_S|, \quad I_R = \frac{2}{\pi} \arg(I_S).
$$

步骤2. 对 J₃ 应用 ξ(S₃) 的逆，以使用所提出的加密技术中的步骤2生成随机掩模R₁ 和R₂。现在，计算它们的复共轭R̄₁ 和R̄₂，因为它们可以消除随机掩模的影响，如下所示：

$$
R_1 \times \bar{R}_1 = \exp\left(i \frac{\pi}{2} J_1^8\right) \times \exp\left(-i \frac{\pi}{2} J_1^8\right) = \exp(0) = 1.
$$

步骤3. 接下来，通过使用以下方程移除随机掩模：

$$
I_g = F^{-1}[F(I_R) \times \bar{R}_2] \times \bar{R}_1.
$$

步骤4. 最后，对Ig应用与g对应的RTS的逆，以恢复秘密图像I。所提出的解密过程的流程图如图1(b)所示。

加密算法流程图。(b) 解密算法流程图。)

4. 安全分析与比较

我们在Matlab中实现了所提出的技术以及其他安全系统，如[10–12, 23, 24, 32–34]所述，并在31幅尺寸为225×225的灰度图像上进行了测试。这些测试图像来自[35]。实验中我们使用Lena图像作为宿主图像。本节的目的是研究并比较所提出的安全算法与一些现有密码系统的强度，这些密码系统基于单S盒或S盒与隐写术的结合。

4.1 客观保真度准则

本实验的目的是测量重建图像与原始图像之间的误差量。如果误差值较大，则密码系统的安全性较高；如果误差值较小，则密码系统的安全性值得怀疑。均方根误差（RMSE）和峰值信噪比（PSNR）是衡量保真度水平的两个常用参数[36–38]。

RMSE和PSNR由以下公式给出：

$$
\text{RMSE} = \sqrt{\frac{\sum_{x=1}^{M} \sum_{y=1}^{N}(I(x,y) - I’(x,y))^2}{M \times N}},
$$

$$
\text{PSNR} = 10 \log_{10} \left[ \frac{(255)^2 \times M \times N}{\sum_{x=1}^{M} \sum_{y=1}^{N}(I(x,y) - I’(x,y))^2} \right],
$$

其中I表示明文图像，I′表示密文图像。

我们对所提出的加密技术及其他安全系统进行了保真度分析。实验结果的比较如图2(a)和2(b)所示。从图2(a)和2(b)可以明显看出，与其他安全技术相比，所提出的密码系统的RMSE值最大，PSNR值最小。因此，该提出的技术在满足客观保真度准则方面比其他密码系统更高效。

RMSE结果与比较。 (b) PSNR结果与比较。)

4.2. 敏感性分析

通常，密码分析者使用差分攻击从密文图像中窃取信息。在此攻击中，图像像素发生微小变化，以分析结果图像中变化的程度。归一化平均变化强度（UACI）用于衡量密码系统抵抗差分攻击的安全性水平[32, 39]。计算UACI的数学表达式如下：

$$
\text{UACI} = \frac{1}{M \times N} \left[ \sum_{x=1}^{M} \sum_{y=1}^{N} \frac{|I(x,y) - I’(x,y)|}{255} \right] \times 100.
$$

本实验的结果如图3所示。从图3可以明显看出，所提出的技术生成的UACI值最大。因此，与其他技术相比，它能有效抵抗差分攻击。

4.3. 相关性和对比度分析

明文图像的像素在水平、垂直和对角方向上具有高度相关性。如果一个密码系统能够显著降低像素之间的相关性并提高对比度，则该系统是安全的。

相关系数 $ r_{xy} $ 通过以下表达式计算：

$$
r_{xy} = \frac{\text{cov}(x,y)}{\sqrt{H(x)}\sqrt{H(y)}},
$$

其中

$$
\text{cov}(x,y) = \frac{1}{M} \sum_{i=1}^{M} (x_i - E(x))(y_i - E(y)),
$$
$$
H(x) = \frac{1}{M} \sum_{i=1}^{M} (x_i - E(x))^2,
$$
$$
E(x) = \frac{1}{M} \sum_{i=1}^{M} x_i.
$$

我们计算了像素在垂直、水平和对角方向的相关性，其结果如图4(a)–4(c)所示。对比度分析的结果显示在图4(d)中。这些图表明，所提出的安全技术产生了最小的相关性和最大的对比度。

垂直相关性结果与对比。(b) 水平相关性结果与对比。(c) 对角相关性结果与对比。(d) 对比度分析结果与对比。)

4.4. 频谱幅度分析

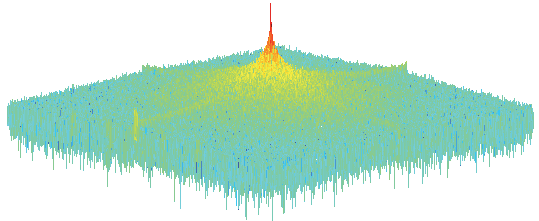
在图像中，频谱分布并不均匀。如果一个密码系统能够均匀地分布频率，并在明文图像和密文图像的频谱之间产生显著差异，则称该密码系统性能良好。我们已在所有31幅图像上进行了此项测试。三个加密图像及其频谱分别如图5(g)–5(i)和图5(j)–5(l)所示。图5(d)–5(f)显示了秘密图像的频谱。需要注意的是，图5(d)–5(f)中的频谱分布集中在每幅图像中间的一个小区域内。通常，这个小区域容易受到安全攻击。从图5(j)–5(l)可以明显看出，所提出方案加密的图像中频率分布均匀，能够抵御统计攻击。

秘密图像。 (b) 秘密图像。 (c) 秘密图像。 (d) (a)的频谱。 (e) (b)的频谱。 (f) (c)的频谱。 (g) (a)的加密。 (h) (b)的加密。(i) (c)的加密。 (j) (g)的频谱。 (k) (h)的频谱。 (l) (i)的频谱。)

5. 结论

在本研究中，我们提出了一种基于RTSs和隐写术的灰度图像加密技术。所提出的密码系统利用多个RTSs和相位嵌入技术，在秘密图像的空间域和频率域中产生混淆。模糊方法用于RTS盒的选择。分析与比较表明，与一些基于单S盒以及S盒与隐写术结合的知名密码系统相比，所提出的安全系统更加安全。未来，经过适当修改后，新开发的算法可用于彩色图像加密和数据隐藏。