[HNCTF 2022 WEEK2]来解个方程?

标准的Z3题，可以拿来当模版题

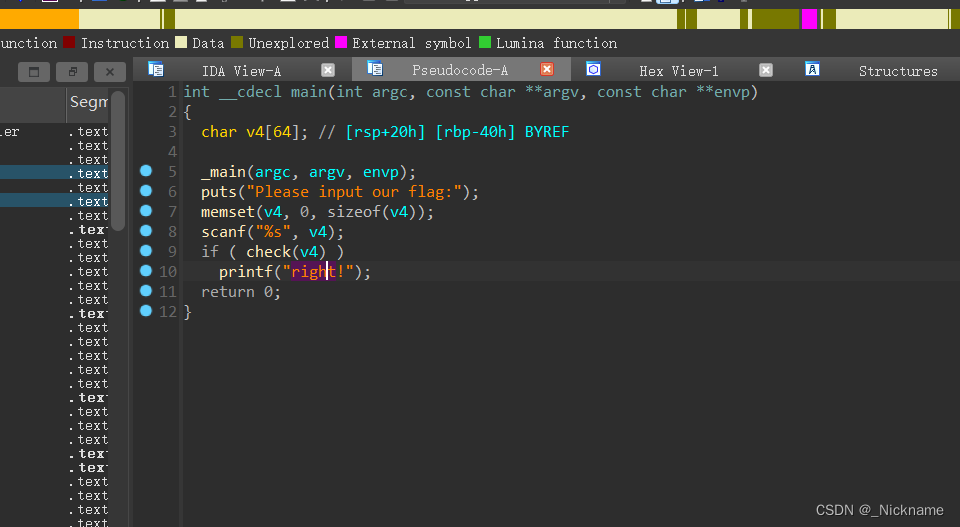
题目逻辑很简单

直接看check

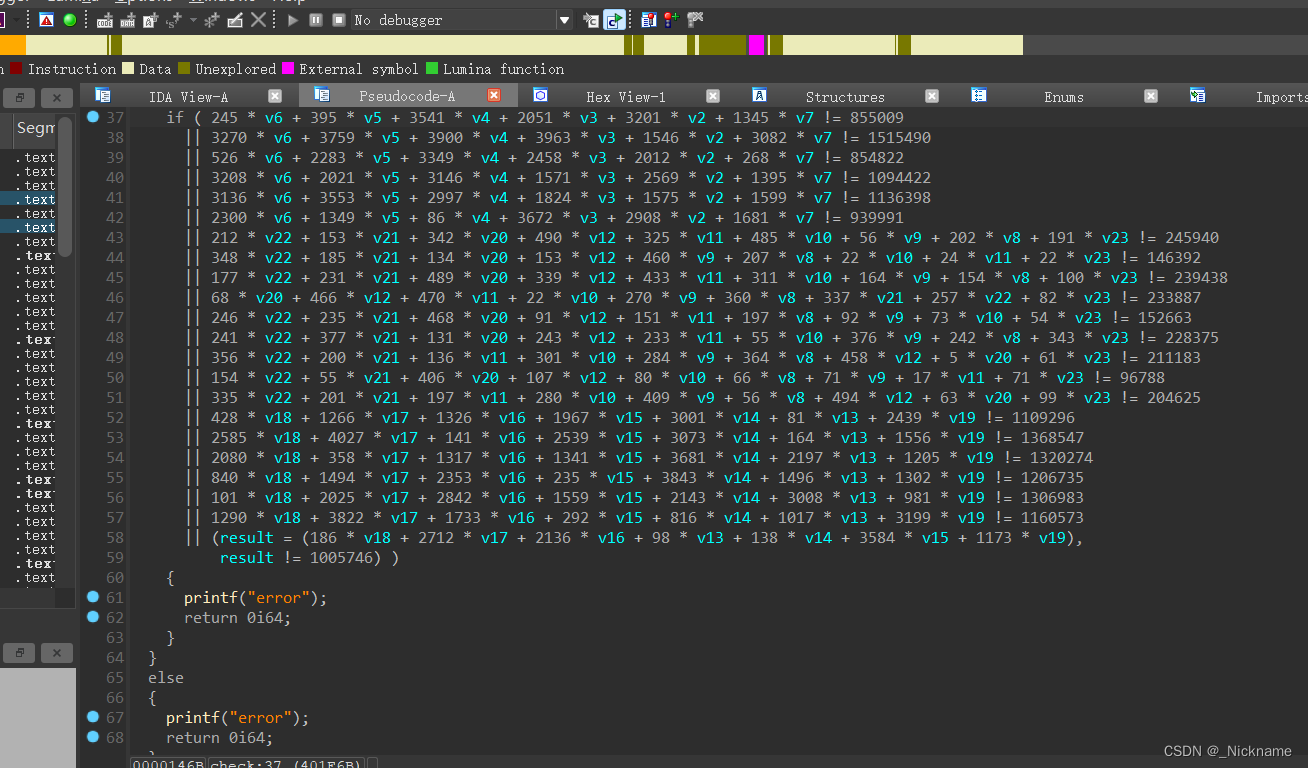
from z3 import *
# 初始化求解器
s = Solver()
# 定义6个未知数
n = 24
x = [Int('s' + str(i)) for i in range(0,24)]
s.add(
    245 * x[6]+ 395 * x[5 ]+ 3541 * x[4 ]+ 2051 * x[3 ]+ 3201 * x[2 ]+ 1345 * x[7 ]== 855009,
    3270 * x[6]+ 3759 * x[5 ]+ 3900 * x[4 ]+ 3963 * x[3 ]+ 1546 * x[2 ]+ 3082 * x[7 ]== 1515490,
    526 * x[6]+ 2283 * x[5 ]+ 3349 * x[4 ]+ 2458 * x[3 ]+ 2012 * x[2 ]+ 268 * x[7 ]== 854822,
    3208 * x[6]+ 2021 * x[5 ]+ 3146 * x[4 ]+ 1571 * x[3 ]+ 2569 * x[2 ]+ 1395 * x[7 ]== 1094422,
    3136 * x[6]+ 3553 * x[5 ]+ 2997 * x[4 ]+ 1824 * x[3 ]+ 1575 * x[2 ]+ 1599 * x[7 ]== 1136398,
    2300 * x[6]+ 1349 * x[5 ]+ 86 * x[4 ]+ 3672 * x[3 ]+ 2908 * x[2 ]+ 1681 * x[7 ]== 939991,
    212 * x[22] + 153 * x[21] + 342 * x[20] + 490 * x[12] + 325 * x[11] + 485 * x[10] + 56 * x[9 ]+ 202 * x[8 ]+ 191 * x[23] == 245940,
    348 * x[22] + 185 * x[21] + 134 * x[20] + 153 * x[12] + 460 * x[9 ]+ 207 * x[8 ]+ 22 * x[10] + 24 * x[11] + 22 * x[23] == 146392,
    177 * x[22] + 231 * x[21] + 489 * x[20] + 339 * x[12] + 433 * x[11] + 311 * x[10] + 164 * x[9 ]+ 154 * x[8 ]+ 100 * x[23] == 239438,
    68 * x[20] + 466 * x[12] + 470 * x[11] + 22 * x[10] + 270 * x[9 ]+ 360 * x[8 ]+ 337 * x[21] + 257 * x[22] + 82 * x[23] == 233887,
    246 * x[22] + 235 * x[21] + 468 * x[20] + 91 * x[12] + 151 * x[11] + 197 * x[8 ]+ 92 * x[9 ]+ 73 * x[10] + 54 * x[23] == 152663,
    241 * x[22] + 377 * x[21] + 131 * x[20] + 243 * x[12] + 233 * x[11] + 55 * x[10] + 376 * x[9 ]+ 242 * x[8 ]+ 343 * x[23] == 228375,
    356 * x[22] + 200 * x[21] + 136 * x[11] + 301 * x[10] + 284 * x[9 ]+ 364 * x[8 ]+ 458 * x[12] + 5 * x[20] + 61 * x[23] == 211183,
    154 * x[22] + 55 * x[21] + 406 * x[20] + 107 * x[12] + 80 * x[10] + 66 * x[8 ]+ 71 * x[9 ]+ 17 * x[11] + 71 * x[23] == 96788,
    335 * x[22] + 201 * x[21] + 197 * x[11] + 280 * x[10] + 409 * x[9 ]+ 56 * x[8 ]+ 494 * x[12] + 63 * x[20] + 99 * x[23] == 204625,
    428 * x[18] + 1266 * x[17] + 1326 * x[16] + 1967 * x[15] + 3001 * x[14] + 81 * x[13] + 2439 * x[19] == 1109296,
    2585 * x[18] + 4027 * x[17] + 141 * x[16] + 2539 * x[15] + 3073 * x[14] + 164 * x[13] + 1556 * x[19] == 1368547,
    2080 * x[18] + 358 * x[17] + 1317 * x[16] + 1341 * x[15] + 3681 * x[14] + 2197 * x[13] + 1205 * x[19] == 1320274,
    840 * x[18] + 1494 * x[17] + 2353 * x[16] + 235 * x[15] + 3843 * x[14] + 1496 * x[13] + 1302 * x[19] == 1206735,
    101 * x[18] + 2025 * x[17] + 2842 * x[16] + 1559 * x[15] + 2143 * x[14] + 3008 * x[13] + 981 * x[19] == 1306983,
    1290 * x[18] + 3822 * x[17] + 1733 * x[16] + 292 * x[15] + 816 * x[14] + 1017 * x[13] + 3199 * x[19] == 1160573,
    186 * x[18] + 2712 * x[17] + 2136 * x[16] + 98 * x[13] + 138 * x[14] + 3584 * x[15] + 1173 * x[19] ==1005746,
)
# 检查是否存在满足条件的解
if s.check() == sat:
    # 输出模型（解）
    print(s.model())
    # 提取有序解并转换为整数列表
    m = s.model()
    ordered_solution = [m[x[i]].as_long() for i in range(2,n)]
    print("按顺序排列的解：", ordered_solution)

a=[78, 83, 83, 67, 84, 70, 123, 112, 105, 112, 95, 105, 110, 115, 116, 64, 108, 108, 95, 90, 51, 125]
for i in a:
    print(chr(i),end='')

重点是代码，建议大家过一遍这个代码