校招算法笔面试 | 校招笔面试真题-山寨金闪闪

原创已于 2025-06-10 09:43:32 修改 · 868 阅读

27 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #面试 #职场和发展 #算法校招 #笔试 #算法校招笔试

于 2025-06-10 09:40:50 首次发布

牛客校招笔面试真题题单题解专栏收录该内容

238 篇文章

订阅专栏

题目## 题目

题目链接

解题思路

对于每个客人分配到的区间 $[l, r]$ ，需要判断能否从中选择三个武器组成三角形
关键是利用三角形的性质：任意两边之和大于第三边
优化策略：
- 当区间长度小于3时，无法形成三角形
- 当区间长度大于等于47时，必定能组成三角形（斐波那契数列）
- 其他情况需要排序后判断相邻的三个数是否能组成三角形

代码

#include<bits/stdc++.h>
using namespace std;
const int MAXN = (int)1e7 + 5;

int main() {
    int n, a[MAXN], m;
    vector<int> v;
    
    while(~scanf("%d", &n)) {
        for(int i = 1; i <= n; i++)
            scanf("%d", &a[i]);
        scanf("%d", &m);
        int cnt = 0;
        
        while(m--) {
            int l, r;
            scanf("%d%d", &l, &r);
            if(r-l+1 >= 47)  // 区间长度≥47必定能组成三角形
                cnt++;
            else if(r-l+1 < 3)  // 区间长度<3不可能组成三角形
                continue;
            else {
                v.clear();
                for(int i = l; i <= r; i++)
                    v.push_back(a[i]);
                sort(v.begin(), v.end());
                int len = v.size();
                for(int i = 0; i < len-2; i++) {
                    if(v[i] + v[i+1] > v[i+2]) {
                        cnt++;
                        break;
                    }
                }
            }
        }
        printf("%d\n", cnt);
    }
    return 0;
}

import java.util.*;

public class Main {
    static final int MAXN = (int)1e7 + 5;
    
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int[] a = new int[MAXN];
        ArrayList<Integer> v = new ArrayList<>();
        
        while(sc.hasNext()) {
            int n = sc.nextInt();
            for(int i = 1; i <= n; i++)
                a[i] = sc.nextInt();
            int m = sc.nextInt();
            int cnt = 0;
            
            while(m-- > 0) {
                int l = sc.nextInt();
                int r = sc.nextInt();
                if(r-l+1 >= 47)
                    cnt++;
                else if(r-l+1 < 3)
                    continue;
                else {
                    v.clear();
                    for(int i = l; i <= r; i++)
                        v.add(a[i]);
                    Collections.sort(v);
                    int len = v.size();
                    for(int i = 0; i < len-2; i++) {
                        if(v.get(i) + v.get(i+1) > v.get(i+2)) {
                            cnt++;
                            break;
                        }
                    }
                }
            }
            System.out.println(cnt);
        }
    }
}

import sys

MAXN = 10**7 + 5
a = [0] * MAXN

for line in sys.stdin:
    n = int(line)
    a[1:n+1] = map(int, input().split())
    m = int(input())
    cnt = 0
    
    for _ in range(m):
        l, r = map(int, input().split())
        if r-l+1 >= 47:
            cnt += 1
        elif r-l+1 < 3:
            continue
        else:
            v = sorted(a[l:r+1])
            len_v = len(v)
            for i in range(len_v-2):
                if v[i] + v[i+1] > v[i+2]:
                    cnt += 1
                    break
    
    print(cnt)

算法及复杂度

算法：排序 + 三角形判定
时间复杂度： $\mathcal{O}(m \cdot n\log n)$ ，其中 $m$ 为客人数量， $n$ 为区间长度
空间复杂度： $\mathcal{O}(n)$ ，需要存储武器数组和临时数组

题目链接

题目描述

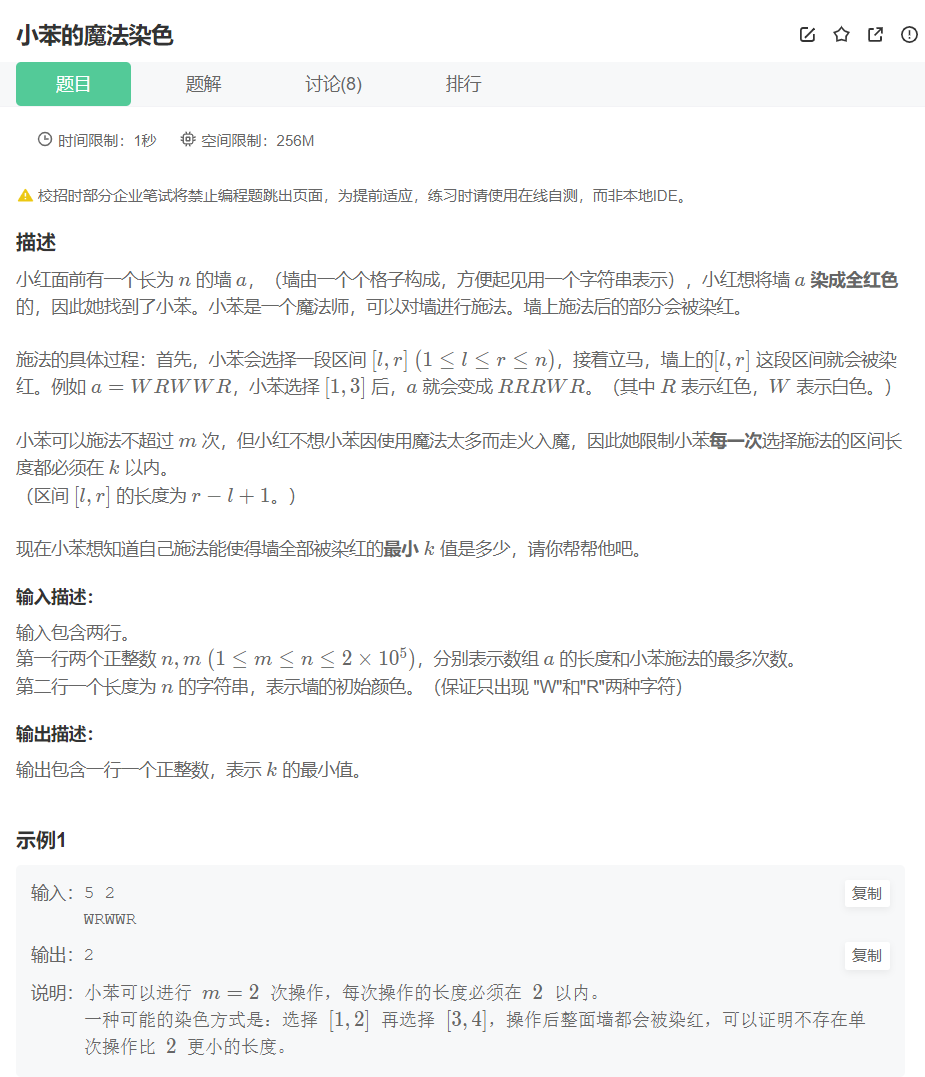
题目地址：24淘天春招-小苯的魔法染色
alt

解题思路

这是一个最小化问题，我们需要找到能将整面墙染红的最小区间长度。关键思路如下：

使用二分查找来寻找最小的区间长度 $k$
对于每个猜测的长度 $k$ ，我们需要验证是否能在最多 $m$ 次操作内将墙完全染红
验证过程中，我们采用贪心策略：
- 从左到右扫描墙面
- 遇到白色格子时，尽可能覆盖最多的未染色区域

代码

#include <iostream>
#include <string>
using namespace std;

bool check(string& s, int m, int k) {
    int n = s.length();
    int count = 0;  // 操作次数
    int i = 0;
    while (i < n) {
        if (s[i] == 'W') {  // 遇到白色需要染色
            count++;
            if (count > m) return false;
            i = i + k;  // 跳过已染色的区域
        } else {
            i++;
        }
    }
    return true;
}

int solve(int n, int m, string& s) {
    int left = 0, right = n + 1;
    int ans = n;
    
    while (left < right) {
        int mid = left + (right - left) / 2;
        if (check(s, m, mid)) {
            ans = mid;
            right = mid;
        } else {
            left = mid + 1;
        }
    }
    return ans;
}

int main() {
    int n, m;
    string s;
    cin >> n >> m >> s;
    cout << solve(n, m, s) << endl;
    return 0;
}

import java.util.Scanner;

public class Main {
    public static boolean check(String s, int m, int k) {
        int n = s.length();
        int count = 0;  // 操作次数
        int i = 0;
        while (i < n) {
            if (s.charAt(i) == 'W') {  // 遇到白色需要染色
                count++;
                if (count > m) return false;
                i = i + k;  // 跳过已染色的区域
            } else {
                i++;
            }
        }
        return true;
    }
    
    public static int solve(int n, int m, String s) {
        int left = 0, right = n + 1;
        int ans = n;
        
        while (left < right) {
            int mid = left + (right - left) / 2;
            if (check(s, m, mid)) {
                ans = mid;
                right = mid;
            } else {
                left = mid + 1;
            }
        }
        return ans;
    }
    
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        int m = sc.nextInt();
        String s = sc.next();
        System.out.println(solve(n, m, s));
        sc.close();
    }
}

def check(s, m, k):
    n = len(s)
    count = 0  # 操作次数
    i = 0
    while i < n:
        if s[i] == 'W':  # 遇到白色需要染色
            count += 1
            if count > m:  # 超过允许的操作次数
                return False
            i = i + k  # 跳过已染色的区域
        else:
            i += 1
    return True

def solve(n, m, s):
    left, right = 0, n + 1
    ans = n
    
    while left < right:
        mid = left + (right - left) // 2
        if check(s, m, mid):
            ans = mid
            right = mid
        else:
            left = mid + 1
            
    return ans

# 读取输入
n, m = map(int, input().split())
s = input()
print(solve(n, m, s))