LeetCode.132 分割回文串 II

最新推荐文章于 2025-03-20 21:53:52 发布

原创最新推荐文章于 2025-03-20 21:53:52 发布 · 85 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#leetcode #算法

力扣题解专栏收录该内容

82 篇文章

订阅专栏

这篇博客详细解析了如何运用动态规划方法解决LeetCode上的回文划分问题（Palindrome Partitioning II）。作者首先介绍了动态规划的基本思路，然后通过创建二维布尔数组记录子串是否为回文，并定义了一个表示子串结束位置的最小分割次数的数组。博客中还提供了具体的Java代码实现，包括如何初始化dp数组和计算最小分割次数。最后，通过示例字符串展示了算法的运行过程。

原题

https://leetcode-cn.com/problems/palindrome-partitioning-ii/

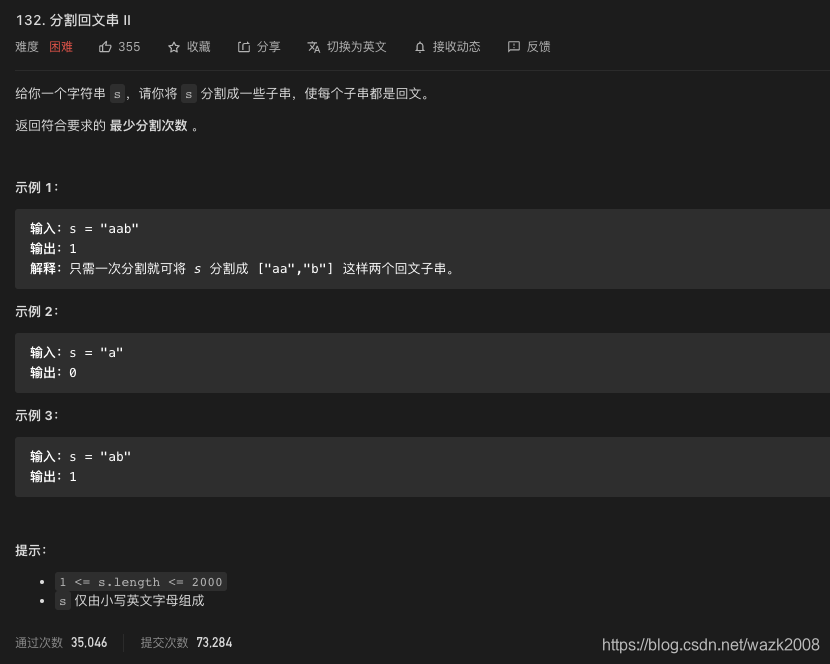
在这里插入图片描述

思路

动态规划
又是该死的动态规划

先用dp数组来保存子串 [i, j] 是否为回文串
再用f{j}函数来表示 j 下标对应结尾的字符串的最小分割次数
- 需要考虑 j 是否会独立占用一次分割
- 先按照需要独立占用一次分割来计算，也就是f[j] = f[j-1] + 1
- 然后从0遍历到 j 的位置，判断是否有对应的 [i, j] 形成回文串，也就是 f[j] = Math.min(f[j], f[i-1]+1)

我这里参考了大佬的解题思路，给大佬粘过来，以表感谢🙏
https://leetcode-cn.com/problems/palindrome-partitioning-ii/solution/xiang-jie-liang-bian-dong-tai-gui-hua-ji-s5xr/

题解

package com.leetcode.code;

/**
 * @Description:
 * @ClassName: Code132
 * @Author: ZK
 * @Date: 2021/3/8 22:16
 * @Version: 1.0
 */
public class Code132 {

    public static void main(String[] args) {
        String s = "aab";
        minCut(s);

    }

//    动态规划
//    1。先用dp数组来保存子串 [i, j] 是否为回文串
//    2。再用f{j}函数来表示 j 下标对应结尾的字符串的最小分割次数
//        需要考虑 j 是否会独立占用一次分割
//        先按照需要独立占用一次分割来计算，然后遍历到 j 的位置，判断是否有对应的 [i, j] 形成回文串，也就是 f[j] = Math.min(f[j], f[i-1]+1);
    public static int minCut(String s) {
        int len = s.length();
        char[] cs = s.toCharArray();

//        动态规划，设置dp数组来保存子串 [i, j] 是否为回文串
        boolean[][] st = new boolean[len][len];
        for (int j = 0; j < len; j++) {
            for (int i = j; i >= 0; i--) {
//                当 [i, j] 只有一个字符时，必然是回文串
                if (i == j) {
                    st[i][j] = true;
                } else {
//                    当 [i, j] 长度为 2 时，满足 cs[i] == cs[j] 即回文串
                    if (j-i == 1) {
                        st[i][j] = cs[i]==cs[j];
                    } else {
//                        当 [i, j] 长度超过 2 时，满足 cs[i]==cs[j] && f[i+1][j-1]==true 即回文串
//                        st[i][j] = cs[i]==cs[j] && cs[i+1]==cs[j-1];
                        st[i][j] = cs[i]==cs[j] && st[i+1][j-1];
                    }
                }
            }
        }

//        设：f{i}函数 代表下标为 i 的字符为结尾的最小分割次数
        int[] f = new int[len];
        for (int j = 1; j < len; j++) {
//            如果 [0, j] 为一个回文串，则无序分割
            if (st[0][j]) {
                f[j] = 0;
            } else {
//                如果 [0, j] 不是一个回文串，那么则依赖于 f[j-1]，即 f[j] = f[j-1]+1
//                注意：此时 j 是需要独立的占用一个分割次数,例如："aabbc"，j=4, f[j] = f[j-1]+1
//                备注：此时先按照 j 需要独立占用一个分割次数来计算，下边进行 min 计算
                f[j] = f[j-1] + 1;

//                但是：如果 j 不需要独立占用一个分割次数，例如："aabb", j=3, f[j]=f[j-1]+1 则错误
//                此时则需要与前边的某个 i 形成区间 [i, j]，使得 [i, j] 回文
                for (int i = 0; i < j; i++) {
                    if (st[i][j]) {
                        f[j] = Math.min(f[j], f[i-1]+1);
                    }
                }
            }
        }

        return f[len-1];
    }

}