LeetCode.51 N 皇后

最新推荐文章于 2025-06-22 21:37:57 发布

原创最新推荐文章于 2025-06-22 21:37:57 发布 · 102 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#leetcode #算法 #递归算法

力扣题解专栏收录该内容

82 篇文章

订阅专栏

本文介绍了如何使用递归回溯法解决LeetCode上的N皇后问题，通过实例展示了如何通过Java代码实现，包括解决方案的逻辑和关键函数的实现细节。

原题

https://leetcode-cn.com/problems/n-queens/

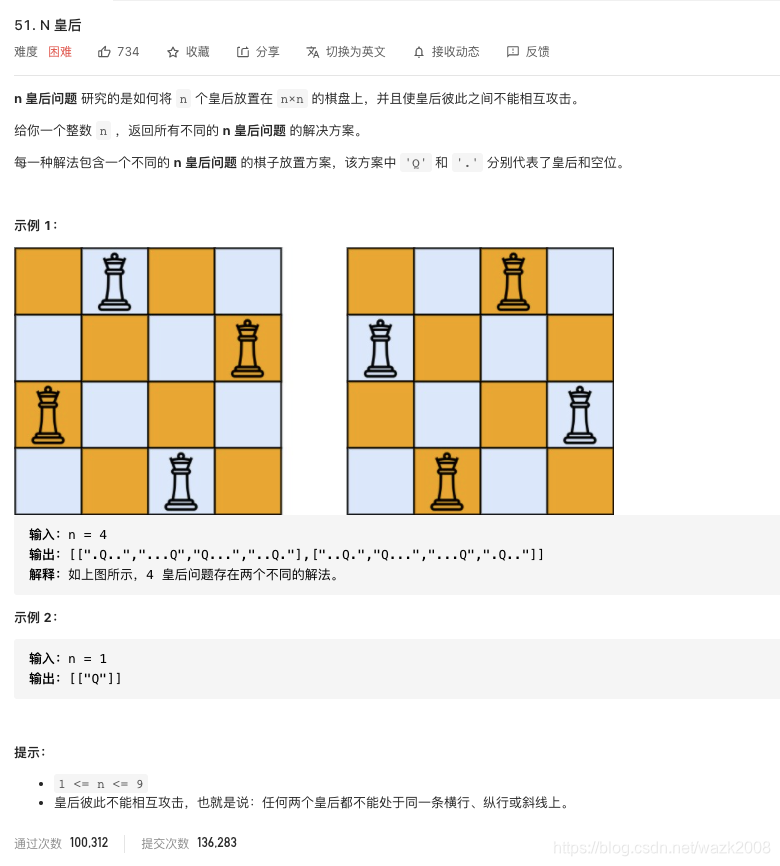
在这里插入图片描述
思路
递归回溯

题解

package com.leetcode.code;

import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;

/**
 * @Description:
 * @ClassName: Code51
 * @Author: ZK
 * @Date: 2021/1/30 14:36
 * @Version: 1.0
 */
public class Code51 {

    public static void main(String[] args) {
        int n = 4;
        List<List<String>> queens = solveNQueens(n);
        System.out.println(queens);
    }

    public static List<List<String>> solveNQueens(int n) {
        List<List<String>> res = new ArrayList<>();
        int[] arr = new int[n];
        solve(res, arr, n, 0);
        return res;
    }

    /**
     * 递归回溯填写8皇后问题
     * @param res   最终返回结果
     * @param arr   记录结果的一维数组，下标i表示第i+1个皇后，arr[i]表示第i+1个皇后在第i+1行的具体纵坐标
     * @param n     n个皇后
     * @param cur   当前在摆放第cur个皇后
     */
    public static void solve(List<List<String>> res, int[] arr, int n, int cur){
//        当前已经摆放到n个皇后，表示n皇后已经摆放完毕
        if ( cur == n) {
//            一维数组的结果转成需要的res集合
            toResult(res, arr);
            return;
        }
//        依次放入皇后，并判断是否发生了冲突
        for (int i = 0; i < n; i++) {
//            把当前这个皇后，依次往0-n的位置摆放，判断是否会发生冲突
            arr[cur] = i;
//            未发生冲突
            if (judge(arr, cur)) {
//                继续向下摆放下一个皇后
                solve(res, arr, n, cur+1);
            }
//            else，发生了冲突，回到循环头部，将当前这个皇后向后摆放一个位置，继续判断是否冲突
        }
    }

    /**
     * 判断放置的第cur个皇后，是否和前边已经摆放好的发生了冲突
     * @param arr   记录结果的一维数组
     * @param cur   当前摆放的第cur个皇后
     * @return      false：有冲突   true：无冲突
     */
    public static boolean judge(int[] arr, int cur){
//        i表示n前边的第几个皇后
        for (int i = 0; i < cur; i++) {
//            arr[i] == arr[cur]  表示同一列是否有冲突
//            Math.abs(cur-i) == Math.abs(arr[cur]-arr[i])  表示统一斜线上是否有冲突
            if (arr[i] == arr[cur] || Math.abs(cur-i) == Math.abs(arr[cur]-arr[i])){
                return false;
            }
        }
        return true;
    }


    /**
     * 一维数组的结果转成需要的res集合
     * @param res   结果需要的res集合
     * @param arr   当前记录结果的一维数组
     */
    public static void toResult(List<List<String>> res, int[] arr){
        int len = arr.length;
        List<String> list = new ArrayList<>();
        for (int i = 0; i < len; i++) {
            char[] chars = new char[len];
            Arrays.fill(chars, '.');
            chars[arr[i]] = 'Q';
            list.add(new String(chars));
        }
        res.add(list);
    }

}