给定n个结点的树，其中有k个结点是特殊结点（未知），定义好结点：该结点到k个特殊结点的距离之和最小。若随机k个结点为特殊结点，求好结点个数的期望值-优快云博客

本文链接：https://blog.youkuaiyun.com/way_back__/article/details/136116495

文章介绍了如何利用并查集数据结构和组合数计算公式解决一个特殊节点问题，当给定节点s值不等于k/2时，通过DFS遍历并计算符合条件的组合数，最终得出答案加一。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

思路：

举例：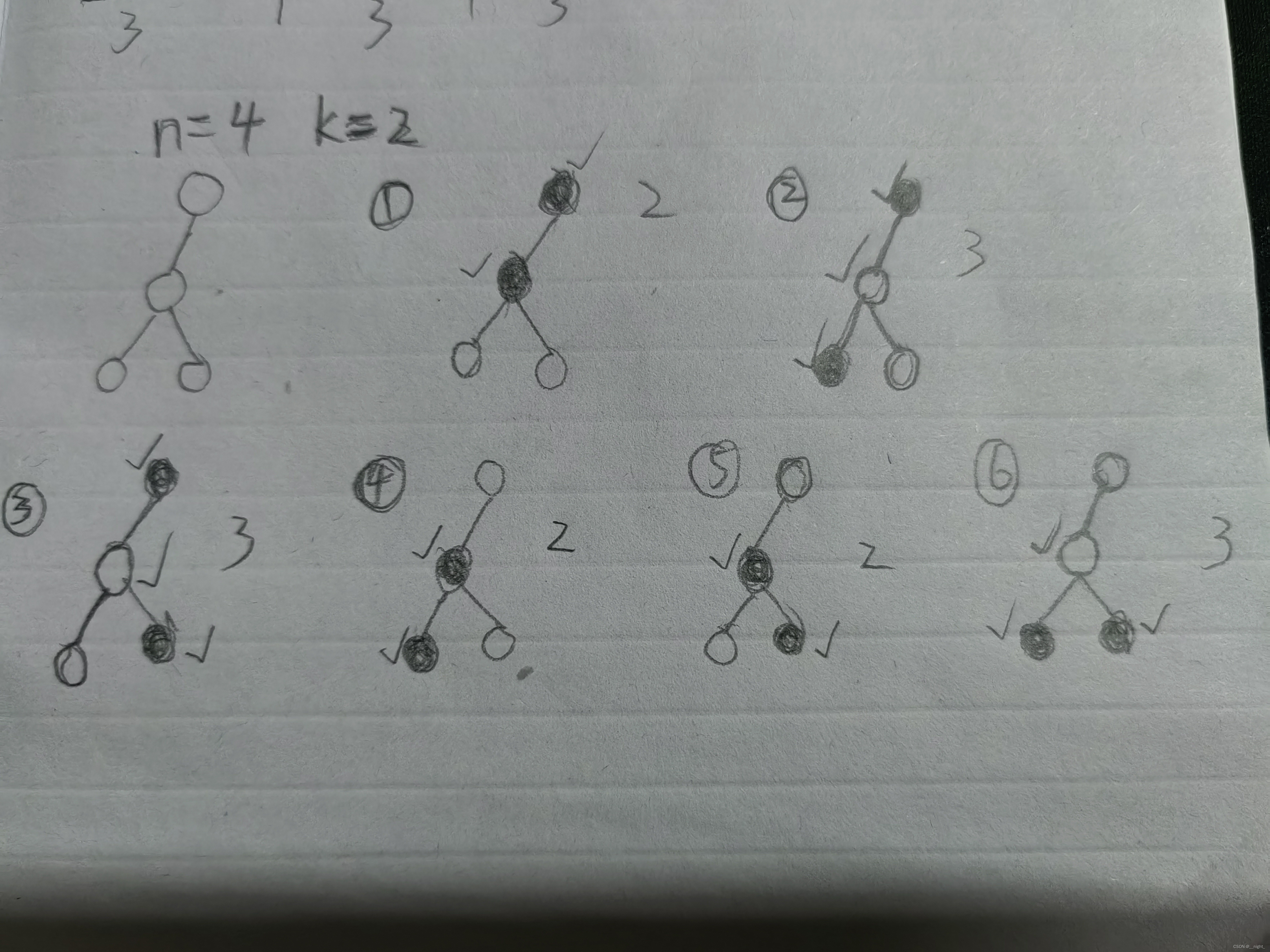

其中黑色结点为特殊结点，可以看出，每种情况都有一个结点的s值不等于k / 2，但是是好结点，所以最后答案加一。

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define pb push_back
#define fi first
#define se second
#define lson p << 1
#define rson p << 1 | 1
const int maxn = 1e6 + 5, inf = 1e18 + 5, maxm = 4e4 + 5, mod = 1e9 + 7, N = 1e6;
int a[maxn], b[maxn];
// bool vis[maxn];
int n, m;
string s;
vector<int> G[maxn];
int siz[maxn];
int fac[maxn], inv[maxn];

int qpow(int a, int b){
	int res = 1;
	while(b){
		if(b & 1) res = res * a % mod;
		a = a * a % mod;
		b >>= 1;
	}
	return res;
}

int C(int n, int m){
	if(n < m) return 0;
	return fac[n] * inv[m] % mod * inv[n - m] % mod;
}


void dfs(int u, int p){
    siz[u] = 1;
    for(auto v : G[u]){
        if(v == p) continue;
        dfs(v, u);
        siz[u] += siz[v];
    }
}

void solve(){
    int res = 0;
    int x, q, k;
    cin >> n >> k;
    for(int i = 1; i < n; i++){
        int u, v;
        cin >> u >> v;
        G[u].pb(v);
        G[v].pb(u);
    }
    if(k % 2 == 1){
        cout << 1 << '\n';
        return;
    }
    dfs(1, 1);
    res = 0;
    for(int i = 1; i <= n; i++){
        res = (res + C(siz[i], k / 2) * C(n - siz[i], k / 2) % mod * qpow(C(n, k), mod - 2) % mod) % mod;
    }
    res = (res + 1) % mod;
    cout << res << '\n';
}
    
signed main(){
    ios::sync_with_stdio(0);
    cin.tie(0);
    fac[0] = 1;
	for(int i = 1; i <= N; i++){
		fac[i] = fac[i - 1] * i % mod;
	}
	inv[N] = qpow(fac[N], mod - 2);
	for(int i = N - 1; i >= 0; i--){
		inv[i] = inv[i + 1] * (i + 1) % mod;
	}
    int T = 1;
    // cin >> T;
    while (T--)
    {
        solve();
    }
    return 0;
}