排序算法的稳定性和源码
稳定性:
所谓稳定性是指当待排序列中有两个或两个以上相同的关键字时,排序前和排序后这些关键字的相对位置,如果没有发生变化就是稳定的,否则就是不稳定的。
如果关键字不能重复,则排序结果是唯一的,那么选择的排序算法稳定与否就无关紧要;如果关键字可以重复,则在选择排序算法是,就要根据具体的需求来考虑选择稳定的还是不稳定的排序算法。
| 排序方式 | 源码链接 | 稳定性 |
|---|---|---|
| 直接插入排序 | 查看源码 | 稳定 |
| 折半插入排序 | 查看源码 | 稳定 |
| 希尔排序 | 查看源码 | 不稳定 |
| 冒泡排序 | 查看源码 | 稳定 |
| 快速排序 | 查看源码 | 不稳定 |
| 简单选择排序 | 查看源码 | 不稳定 |
| 堆排序 | 查看源码 | 不稳定 |
| 二路归并排序 | 查看源码 | 稳定 |
| 基数排序 | 查看源码 | 稳定 |
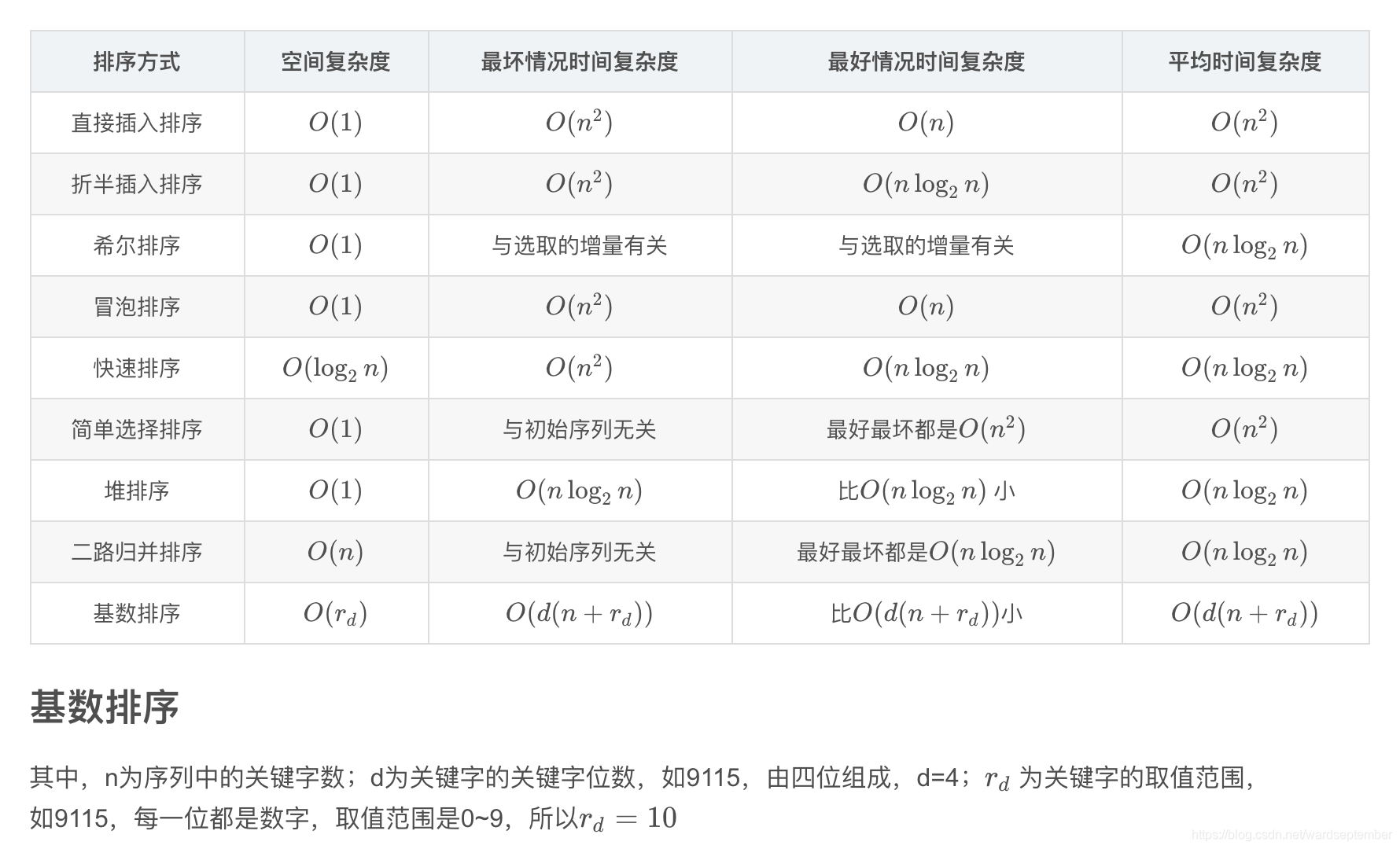
排序算法的空间、时间复杂度
| 排序方式 | 空间复杂度 | 最坏情况时间复杂度 | 最好情况时间复杂度 | 平均时间复杂度 |
|---|---|---|---|---|
| 直接插入排序 | O ( 1 ) O(1) O(1) | O ( n 2 ) O(n^2) O(n2) | O ( n ) O(n) O(n) | O ( n 2 ) O(n^2) O(n2) |
| 折半插入排序 | O ( 1 ) O(1) O(1) | O ( n 2 ) O(n^2) O(n2) | O ( n log 2 n ) O(n\log_{2} n) O(nlog2n) | O ( n 2 ) O(n^2) O(n2) |
| 希尔排序 | O ( 1 ) O(1) O(1) | 与选取的增量有关 | 与选取的增量有关 | O ( n log 2 n ) O(n\log_{2} n) O(nlog2n) |
| 冒泡排序 | O ( 1 ) O(1) O(1) | O ( n 2 ) O(n^2) O(n2) | O ( n ) O(n) O(n) | O ( n 2 ) O(n^2) O(n2) |
| 快速排序 | O ( log 2 n ) O(\log_{2} n) O(log2n) | O ( n 2 ) O(n^2) O(n2) | O ( n log 2 n ) O(n\log_{2} n) O(nlog2n) | O ( n log 2 n ) O(n\log_{2} n) O(nlog2n) |
| 简单选择排序 | O ( 1 ) O(1) O(1) | 与初始序列无关 | 最好最坏都是 O ( n 2 ) O(n^2) O(n2) | O ( n 2 ) O(n^2) O(n2) |
| 堆排序 | O ( 1 ) O(1) O(1) | O ( n log 2 n ) O(n\log_{2} n) O(nlog2n) | 比 O ( n log 2 n ) O(n\log_{2} n) O(nlog2n) 小 | O ( n log 2 n ) O(n\log_{2} n) O(nlog2n) |
| 二路归并排序 | O ( n ) O(n) O(n) | 与初始序列无关 | 最好最坏都是 O ( n log 2 n ) O(n\log_{2} n) O(nlog2n) | O ( n log 2 n ) O(n\log_{2} n) O(nlog2n) |
| 基数排序 | O ( r d ) O(r_d) O(rd) | O ( d ( n + r d ) ) O(d(n+r_d)) O(d(n+rd)) | 比 O ( d ( n + r d ) ) O(d(n+r_d)) O(d(n+rd))小 | O ( d ( n + r d ) ) O(d(n+r_d)) O(d(n+rd)) |
基数排序
其中,n为序列中的关键字数;d为关键字的关键字位数,如9115,由四位组成,d=4;
r
d
r_d
rd 为关键字的取值范围,
如9115,每一位都是数字,取值范围是0~9,所以
r
d
=
10
r_d=10
rd=10
外部排序
- 时间复杂度
外部排序时间复杂度涉及很多方面,且分析起来较为复杂,对于考研注意以下几个方面即可:
- m个初始归并段进行k路归并,归并躺数为 l o g k m log_k m logkm向上取整。
- 每一次归并,所有记录都要进行两次I/O操作。
- 置换——选择排序这一步中,所有记录都要进行两次I/O操作。
- k路归并的败者树的高度为(向上取整)
l
o
g
2
(
k
+
1
)
log_2(k+1)
log2(k+1),
因此利用败者树从k个记录中选出最值需要进行 l o g 2 k log_2 k log2k(向上取整)次比较,
即时间复杂度是 O ( l o g 2 k ) O(log_2 k) O(log2k)。 - k路归并败者树的建树时间复杂度为 O ( k l o g 2 k ) O(klog_2 k) O(klog2k)。
- 空间复杂度
O(1)
各种排序算法的应用场景
- 当n <= 50时,适合适用直接插入排序和简单选择排序,如果元素包含的内容过大,就不适合直接插入排序,因为直接插入排序需要移动元素的次数比较多。
- 当数组基本有序的情况下适合使用直接插入排序和冒泡排序,它们在基本有序的情况下排序的时间复杂度接近 O ( n ) O(n) O(n)。
- 若n较大,则应采用时间复杂度为
O
(
n
log
2
n
)
O(n\log_{2} n)
O(nlog2n)的排序方法:快速排序、堆排序或归并排序。
当待排序的关键字是随机分布、较复杂时,快速排序的平均时间最短。
堆排序所需的辅助空间少于快速排序,并且不会出现快速排序可能出现的最坏情况。
若要求排序稳定,则可选用归并排序。但前面介绍的从单个记录起进行两两归并的排序算法并不值得提倡,通常可以将它和直接插入排序结合在一起使用。先利用直接插入排序求得较长的有序子序列,然后再两两归并之。因为直接插入排序是稳定 的,所以改进后的归并排序仍是稳定的。 - 快速排序,归并排序,希尔排序,堆排序平均时间复杂度都是
O
(
n
log
2
n
)
O(n\log_{2} n)
O(nlog2n)
其中,快速排序是最好的,其次是归并和希尔,堆排序在数据量很大时效果明显(堆排序适合处理大数据)。
大数据处理的一个例子:找出一千万个数中最小的前一百个数。思路:建立一百个节点的大顶堆,首先将前一百个数放入堆中,之后每放入一个数就删除一个堆顶元素,最后剩下的就是最小的一百个数。
这四种排序可看作为“先进算法”,其中,快排效率最高(大数据就不行了,而且速度有概率性),但在待排序列基本有序 的情况下,会变成冒泡排序,接近 O ( n 2 ) O(n^2) O(n2).
希尔排序对增量的标准没有较为满意的答案,增量对性能会有影响。
归并排序效率非常不错,在数据规模较大的情况下,比希尔排序和堆排序要好。
多数先进的算法都是因为跳跃式的比较,降低了比较次数,但牺牲了排序的稳定 性。 - 希尔排序:n较小时较好,且关键字较为复杂较好。
- 基数排序:n较大时较好,且关键字较为复杂较好。





















 3546
3546

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








