 4.二叉树链式结构的实现
4.二叉树链式结构的实现
4.1二叉树链式结构的遍历
遍历(Traversal):
按照某种规则,对二叉树中的每个节点进行相应的操作(打印、每个节点值+1),并且每个节点只能操作一次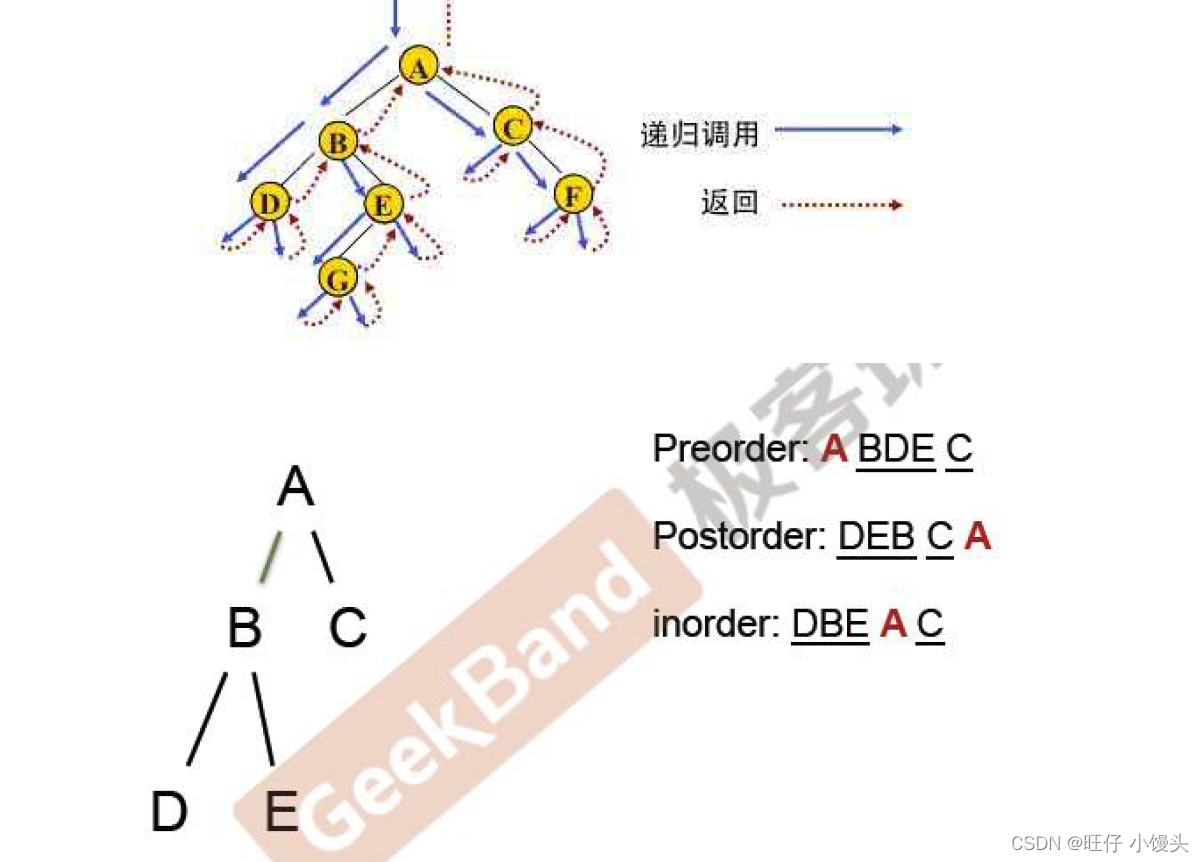
前序 / 中序 / 后序 的递归结构遍历:是根据访问结点操作发生位置命名
1. NLR:前序遍历—— : 根节点-----根节点的左子树-----根节点的右子树 根左右

假设:遍历操作就是将节点中的值域打印出来
遍历顺序 :
1 :打印1 6 : ① —>right : 打印4
2 : ① —>left 打印 2 7 : ④ —>left : 打印5
3 : ② —>left : 打印 3 8 : ⑤—>left /right: 无
4 : ③ —>left /right :无 9 : ④—>right: 打印6
5 : ② —>right : 无 10 : ⑥—>left /right: 无 遍历全部结束
2. LNR:中序遍历—— 根节点的左子树-----根节点-----根节点的右子树 左根右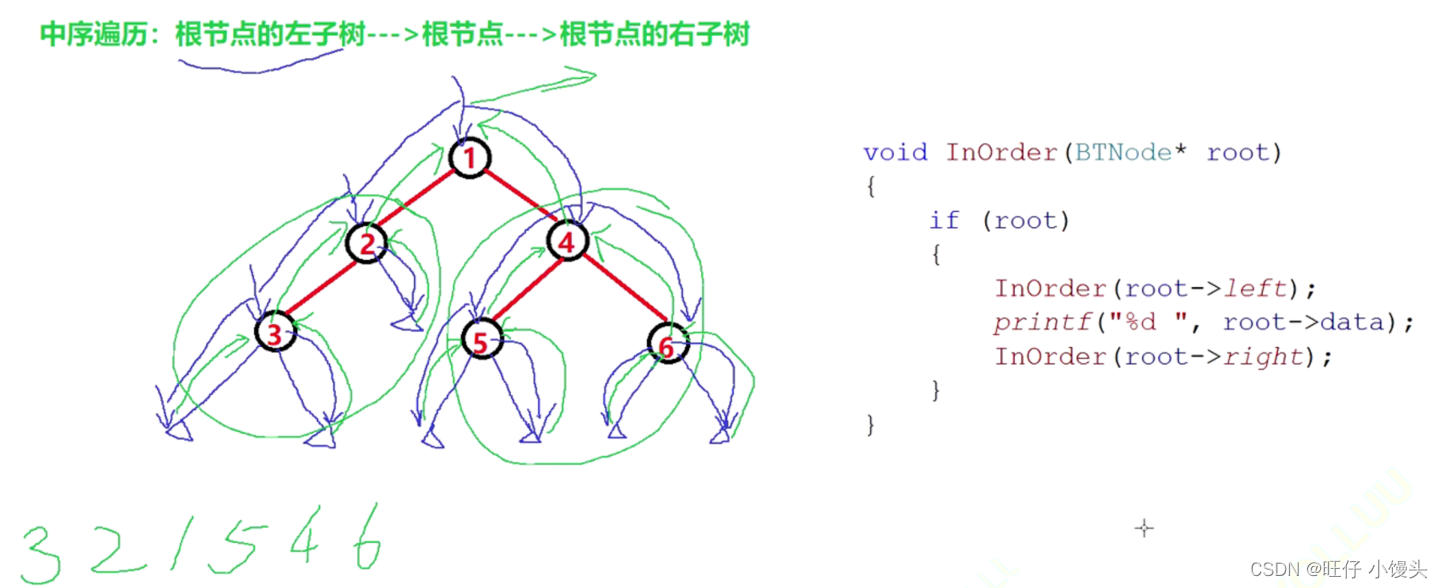
遍历顺序 :
1 :① —>left ② 9 : ①—>right: ④ 17 :⑥ : 打印 6
2 : ② —>left ③ 10 :④—>left: ⑤ 18 :⑥—>right: null
3 : ③ —>left :null 11 : ⑤—>left: null
4 : ③ :打印 3 12 : ⑤ : 打印 5
5 : ③ —>right : 无 13 : ⑤—>right: null
6 : ② :打印 2 14 :④ : 打印 ④
7 : ② —>right: null 15 :④—>right: ⑥
8 : ① : 打印 1 16 :⑥—>left: null
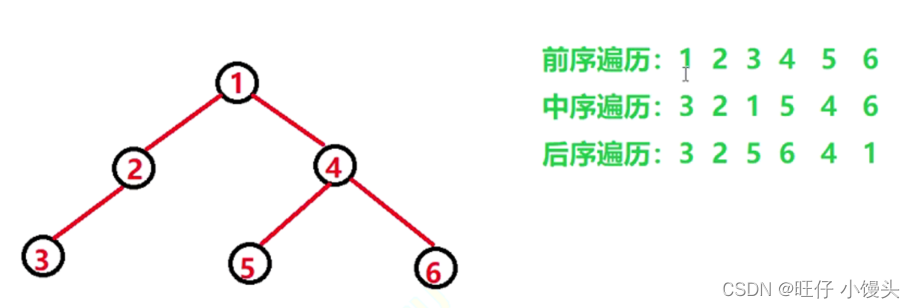
3. LRN:后序遍历—— 根节点的左子树-----根节点的右子树-----根节点 左右根
同理:
void PostOrder(BTNode * root)
{
if(root)
{
PostOrder(root->left);
PostOrder(root->right);
printf("%d", root->data);
}
}
BinaryTree.h
#pragma once
/*创建二叉树的节点的数据类型 binary tree node data type*/
typedef int BTNDataType;
/*创建二叉树的节点类型*/
typedef struct BTNode
{
BTNode* left;
BTNode* right;
BTNDataType data;
}BTNode;// BTNode 是结构体类型struct BTNode的别名
/*创建二叉树节点*/
BTNode* BuyBinTreeNode(BTNDataType data);
/*创建二叉树的函数*/
BTNode* CreatBinTree();
/*前序遍历*/
void PreOrder(BTNode * root);
/*中序遍历*/
void InOrder(BTNode* root);
/*后续遍历*/
void PostOrder(BTNode* root);
void TestBinTree();BinaryTree.cpp
#include "BinaryTree.h"
#include<malloc.h>
#include<iostream>
#include<assert.h>
using namespace std;
/*创建二叉树节点*/
BTNode* BuyBinTreeNode(BTNDataType data)
{
BTNode* newNode = (BTNode*)malloc(sizeof(BTNode));
if (NULL == newNode)
{
assert(0);
return NULL;
}
newNode->data = data;
newNode->left = NULL;
newNode->right = NULL;
return newNode;
}
BTNode* CreatBinTree()
{
BTNode* root = NULL;
BTNode* n1 = BuyBinTreeNode(1);
BTNode* n2 = BuyBinTreeNode(2);
BTNode* n3 = BuyBinTreeNode(3);
BTNode* n4 = BuyBinTreeNode(4);
BTNode* n5 = BuyBinTreeNode(5);
BTNode* n6 = BuyBinTreeNode(6);
root = n1;
n1->left = n2;
n2->left = n3;
n1->right = n4;
n4->left = n5;
n4->right = n6;
return root;
}
void PreOrder(BTNode* root)
{
if (root)
{
printf("%d ", root->data);
PreOrder(root->left);
PreOrder(root->right);
}
}
void InOrder(BTNode* root)
{
if (root)
{
InOrder(root->left);
printf("%d ", root->data);
InOrder(root->right);
}
}
void PostOrder(BTNode* root)
{
if (root)
{
PostOrder(root->left);
PostOrder(root->right);
printf("%d ", root->data);
}
}
void TestBinTree()
{
BTNode* root = CreatBinTree();
cout << "前序遍历结果 ";
PreOrder(root);
cout << endl;
cout << "中序遍历结果 ";
InOrder(root);
cout << endl;
cout << "后序遍历结果 ";
PostOrder(root);
return;
}二叉树的遍历.cpp
#include "BinaryTree.h"
int main()
{
TestBinTree();
return 0 ;
}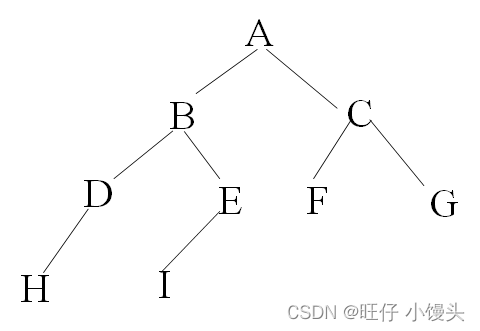
如上图:
前序排列 :根左右 A (根) B(左) C(右)
A B C → ABDEC → ABDECFG → ABDHEICFG
中序排列 :左根右 B A C → D B E A C → DBEA FCG → DBEA FCG →H DB I EA FCG
后序排列 :左右根 B C A → DEBCA → DEBFGCA → HDIEBFGCA
从后续遍历结果中找:树的根
从中序遍历中区分:根节点的左右子树 ,根节点之前的就是左子树,根节点之后的就是右子树
层序遍历:除了先序遍历、中序遍历、后序遍历外,还可以对二叉树进行层序遍历。设二叉树的根节点所在层数为1,层序遍历就是从所在二叉树的根节点出发,首先访问第一层的树根节点,然后从左到右访问第2层上的节点,接着是第三层的节点,以此类推,自上而下,自左至右逐层访问树的结点的过程就是层序遍历

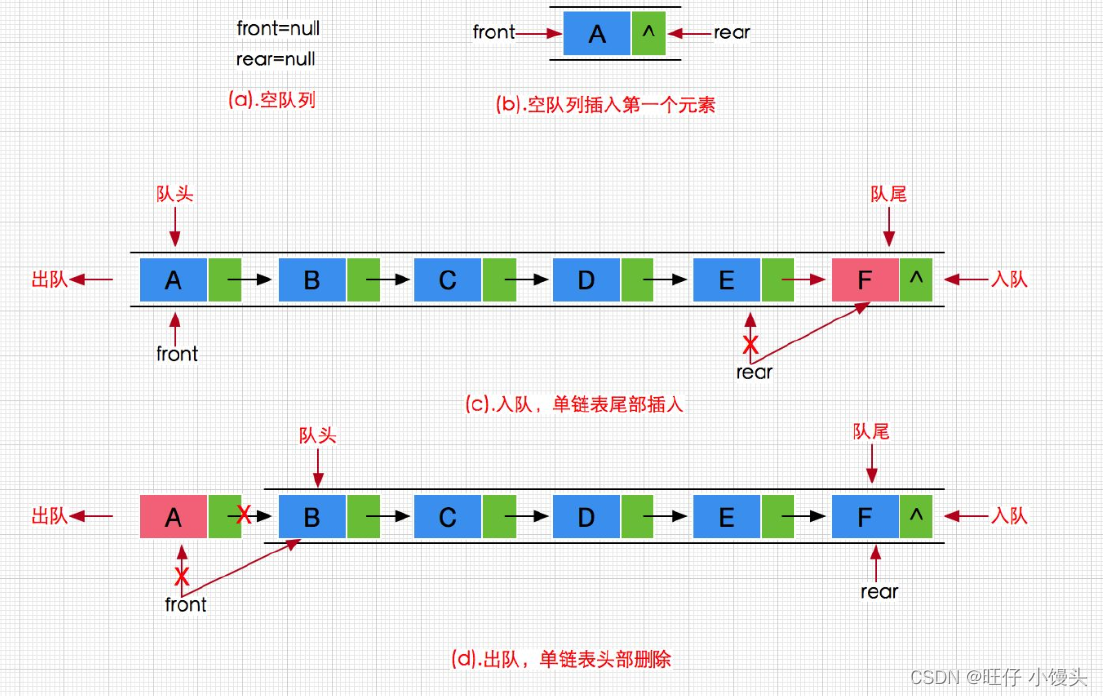
队列:只允许在一端进行插入数据操作,在另一端进行删除数据操作的特殊线性表,队列具有先进先出的特性:入队列 :进行插入操作的一端称为队尾rear
出队列 :进行删除操作的一端称为队头front

Queue.h
#pragma once
// 队列底层采用连续空间来实现,效果不是很好
// 队列:采用链表的方式实现的
/*QDataType:队列中节点的数据类型,这里存放的是一个二叉树的节点并不是一个简单的整型*/
typedef struct BTNode* QDataType;
/*创建队列中的节点类型*/
typedef struct QNode
{
struct QNode* next; // 链式存储都有指针域指向后继节点
QDataType data; // 数据为二叉树节点
}QNode;
typedef struct Queue
{
QNode* front;
QNode* rear;
int size;
}Queue;
// 初始化队列
void QueueInit(Queue* q);
// 队尾入队列
void QueuePush(Queue* q, QDataType data);
// 队头出队列
void QueuePop(Queue* q);
// 获取队列头部元素
QDataType QueueFront(Queue* q);
// 获取队列头部元素
QDataType QueueBack(Queue* q);
// 获取队列中有效元素个数
int QueueSize(Queue* q);
// 检测队列是否为空,如果为空返回非零结果,如果非空返回0
int QueueEmpty(Queue* q);
// 销毁队列
void QueueDestroy(Queue* q);Queue.cpp
#include "Queue.h"
#include <malloc.h>
#include <assert.h>
#include <stdio.h>
QNode* BuyQNode(QDataType data)
{
QNode* newNode = (QNode*)malloc(sizeof(QNode));
if (NULL == newNode)
{
assert(0);
return NULL;
}
newNode->data = data;
newNode->next = NULL;
return newNode;
}
void QueueInit(Queue* q)
{
assert(q);
q->front = NULL;
q->rear = NULL;
q->size = 0;
}
void QueuePush(Queue* q, QDataType data)
{
QNode* newNode = BuyQNode(data);
// 链表尾插
if (QueueEmpty(q))
{
q->front = newNode;
}
else
{
q->rear->next = newNode;
}
q->rear = newNode;
q->size++;
}
void QueuePop(Queue* q)
{
QNode* delNode = NULL;
if (QueueEmpty(q))
return;
delNode = q->front;
if (q->front == q->rear)
q->front = q->rear = NULL;
else
q->front = delNode->next;
free(delNode);
q->size--;
}
QDataType QueueFront(Queue* q)
{
assert(!QueueEmpty(q));
return q->front->data;
}
QDataType QueueBack(Queue* q)
{
assert(!QueueEmpty(q));
return q->rear->data;
}
int QueueSize(Queue* q)
{
assert(q);
return q->size;
}
int QueueEmpty(Queue* q)
{
assert(q);
return NULL == q->front;
}
void QueueDestroy(Queue* q)
{
assert(q);
QNode* cur = q->front;
while (cur)
{
q->front = cur->next;
free(cur);
cur = q->front;
}
q->front = q->rear = NULL;
q->size = 0;
}BinaryTree.h
#pragma once
/*层序遍历*/
void LevelOrder(BTNode* root);
void TestBinTree();BinaryTree.cpp
#include "BinaryTree.h"
#include "Queue.h"
#include<malloc.h>
#include<iostream>
#include<assert.h>
using namespace std;
/*创建二叉树节点*/
BTNode* BuyBinTreeNode(BTNDataType data)
{
BTNode* newNode = (BTNode*)malloc(sizeof(BTNode));
if (NULL == newNode)
{
assert(0);
return NULL;
}
newNode->data = data;
newNode->left = NULL;
newNode->right = NULL;
return newNode;
}
BTNode* CreatBinTree()
{
BTNode* root = NULL;
BTNode* n1 = BuyBinTreeNode(1);
BTNode* n2 = BuyBinTreeNode(2);
BTNode* n3 = BuyBinTreeNode(3);
BTNode* n4 = BuyBinTreeNode(4);
BTNode* n5 = BuyBinTreeNode(5);
BTNode* n6 = BuyBinTreeNode(6);
root = n1;
n1->left = n2;
n2->left = n3;
n1->right = n4;
n4->left = n5;
n4->right = n6;
return root;
}
void LevelOrder(BTNode* root)
{
Queue q;
QueueInit(&q);
QueuePush(&q, root); // 1. 将根节点入队列
while (!QueueEmpty(&q)) // 当队列不为空时, 便有元素没遍历完
{
BTNode* cur = QueueFront(&q);
cout << cur->data<<" "; // 2. 取队头元素front的值域(二叉树节点),访问打印
QueuePop(&q); // 3.将队中元素出列,
if (cur->left) // 4.如果该二叉树结点的左孩子存在---->将其左孩子入队列
QueuePush(&q, cur->left);
if (cur->right) // 5.如果该二叉树结点的右孩子存在---->将其右孩子入队列
QueuePush(&q, cur->right);
}
}
void TestBinTree()
{
BTNode* root = CreatBinTree();
cout << "前序遍历结果: ";
PreOrder(root);
cout << endl;
cout << "中序遍历结果: ";
InOrder(root);
cout << endl;
cout << "后序遍历结果: ";
PostOrder(root);
cout << endl;
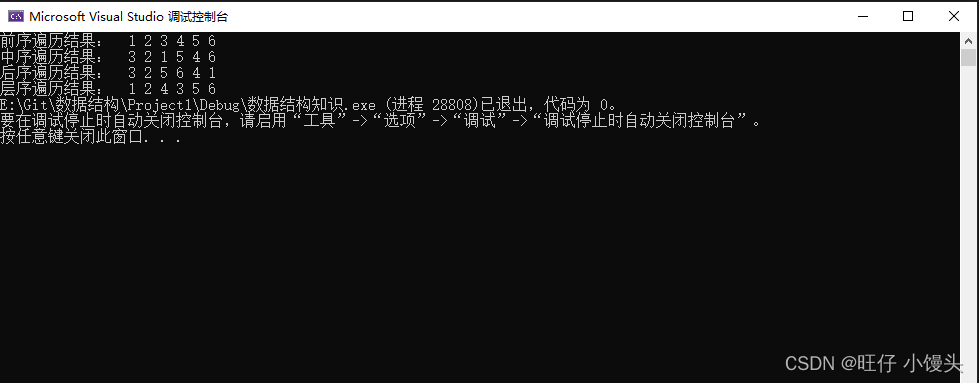
cout << "层序遍历结果: ";
LevelOrder(root);
return;
}
4.2 二叉树的基础面试题
1. 单值二叉树。力扣OJ965
2. 二叉树最大深度。 力扣OJ104
3. 翻转二叉树。力扣OJ226
4. 检查两颗树是否相同。力扣OJ100
5. 对称二叉树。力扣OJ101
6. 二叉树的前序遍历。 力扣OJ144
7. 二叉树中序遍历 。 力扣OJ94
8. 二叉树的后序遍历 。力扣OJ145
9. 另一颗树的子树。 力扣OJ572
10. 判断一颗二叉树是否是平衡二叉树。力扣OJ110
11. 二叉树的构建及遍历。牛客OJ
4.3 二叉树的基础面试题补充(没有合适的OJ)
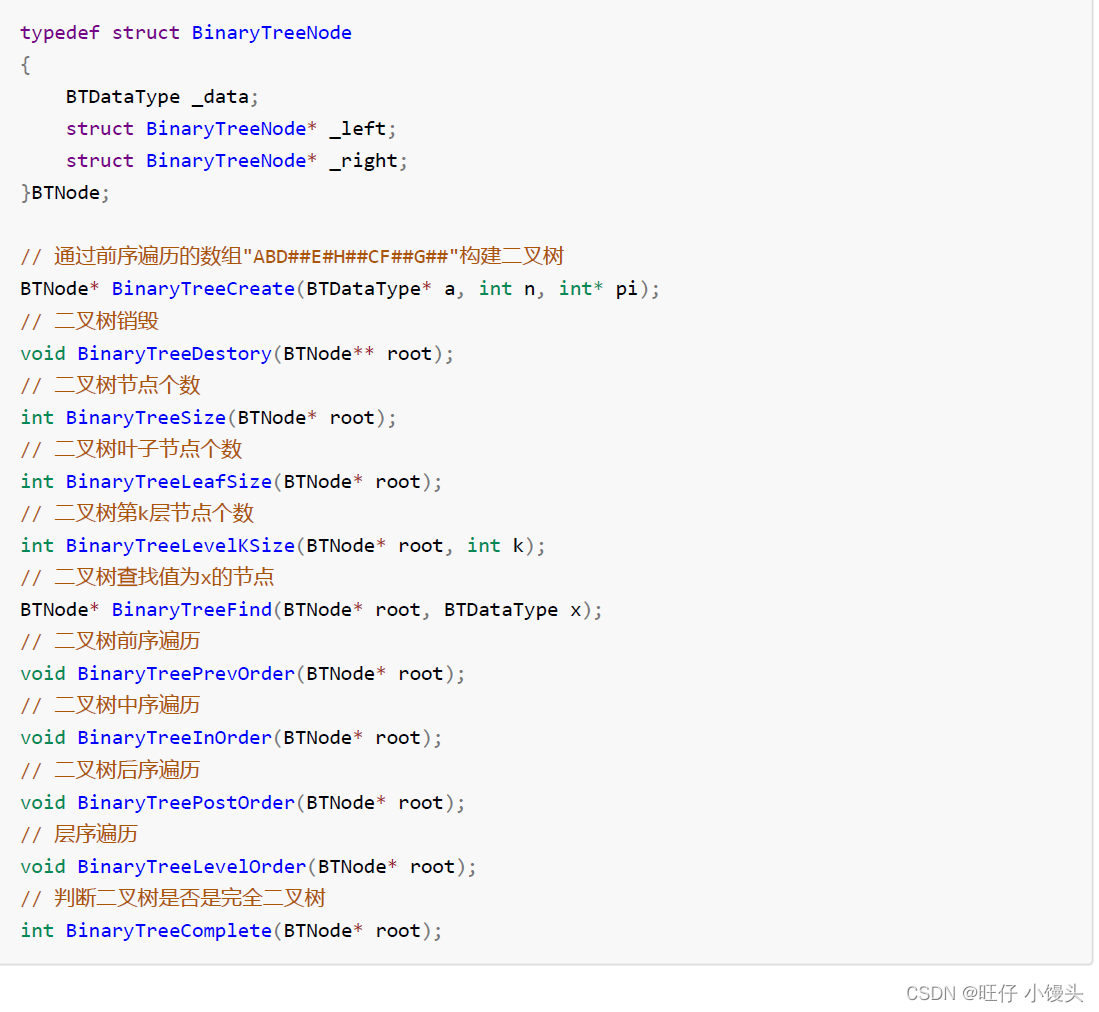




 本文详细介绍了二叉树的链式结构实现,包括前序、中序、后序遍历的递归算法,并提供了层序遍历的实现。此外,文章还列举了一些常见的二叉树面试题目,如单值二叉树、最大深度、翻转等。通过这些内容,读者可以深入理解二叉树的操作和遍历方法。
本文详细介绍了二叉树的链式结构实现,包括前序、中序、后序遍历的递归算法,并提供了层序遍历的实现。此外,文章还列举了一些常见的二叉树面试题目,如单值二叉树、最大深度、翻转等。通过这些内容,读者可以深入理解二叉树的操作和遍历方法。
















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








