Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 5804 Accepted Submission(s): 2192
Total Submission(s): 5804 Accepted Submission(s): 2192
Problem Description
There are a lot of trees in an area. A peasant wants to buy a rope to surround all these trees. So at first he must know the minimal required length of the rope. However, he does not know how to calculate it. Can you help him?
The diameter and length of the trees are omitted, which means a tree can be seen as a point. The thickness of the rope is also omitted which means a rope can be seen as a line.
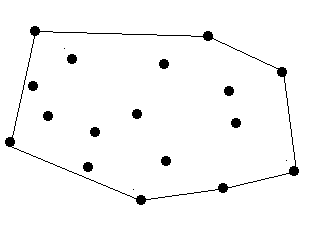
There are no more than 100 trees.
The diameter and length of the trees are omitted, which means a tree can be seen as a point. The thickness of the rope is also omitted which means a rope can be seen as a line.

There are no more than 100 trees.
Input
The input contains one or more data sets. At first line of each input data set is number of trees in this data set, it is followed by series of coordinates of the trees. Each coordinate is a positive integer pair, and each integer is less than 32767. Each pair is separated by blank.
Zero at line for number of trees terminates the input for your program.
Zero at line for number of trees terminates the input for your program.
Output
The minimal length of the rope. The precision should be 10^-2.
Sample Input
9 12 7 24 9 30 5 41 9 80 7 50 87 22 9 45 1 50 7 0
Sample Output
243.06
Source
Asia 1997, Shanghai (Mainland China)
思考:比较赤裸裸的凸包入门题目,注意n=1和n=2的情况,我感觉n个点共线也是一直情况,可能数据比较弱吧。
思考:比较赤裸裸的凸包入门题目,注意n=1和n=2的情况,我感觉n个点共线也是一直情况,可能数据比较弱吧。
#include <iostream>
#include <cmath>
#include <algorithm>
#include <cstdio>
#include <cstring>
#include <vector>
using namespace std;
//Accepted 1392 125MS 280K 2448 B C++
const double eps = 1e-8;
int dcmp(double x) {
if(fabs(x) < eps) return 0;
if(x > 0) return 1;
return -1;
}
struct point {
double x, y;
point() {}
point(double a, double b) : x(a), y(b) {}
friend point operator - (const point a, const point b) {
return point(a.x-b.x, a.y-b.y);
}
};
double det(const point &a, const point &b) {
return a.x * b.y - a.y * b.x;
}
bool comp_less(const point &a, const point &b) {
return dcmp(a.x-b.x)<0 || (dcmp(a.x-b.x)==0 && dcmp(a.y-b.y)<0);
}
bool cmp(const point &a, const point &b) {
if(a.x==b.x && a.y==b.y) return true;
else return false;
}
double dist(const point &a, const point &b) {
return sqrt((a.x-b.x)*(a.x-b.x) + (a.y-b.y)*(a.y-b.y));
}
struct polygon_convex {
vector <point> P;
polygon_convex(int Size = 0) {
P.resize(Size);
}
};
polygon_convex convex_hull(vector<point> a) {
polygon_convex res(2*a.size()+5);
sort(a.begin(), a.end(), comp_less);
///a.erase(unique(a.begin(), a.end()), a.end());
a.erase(unique(a.begin(), a.end(), cmp), a.end());
int m = 0;
for(int i = 0; i < (int)a.size(); ++i) {
while(m > 1 && dcmp(det(res.P[m-1]-res.P[m-2], a[i]-res.P[m-2]))<=0)
--m;
res.P[m++] = a[i];
}
int k = m;
for(int i = int(a.size())-2; i >= 0; --i) {
while(m > k && dcmp(det(res.P[m-1]-res.P[m-2], a[i]-res.P[m-2]))<=0)
--m;
res.P[m++] = a[i];
}
res.P.resize(m);
if(a.size()>1) res.P.resize(m-1);
return res;
}
int main()
{
int n;
point tmp;
vector <point> v(1000);
while(scanf("%d", &n) ==1 && n) {
v.clear();
for(int i = 0; i < n; i++) {
scanf("%lf%lf", &tmp.x, &tmp.y);
v.push_back(tmp);
}
double res = 0.0;
if(n==2) {
res = dist(v[0], v[1]);
printf("%.2lf\n", res);
continue;
}
polygon_convex result;
result = convex_hull(v);
int len = (int)result.P.size();
for(int i = 0; i < len; i++) {
res = res + dist(result.P[i], result.P[(i+1)%len]);
}
printf("%.2lf\n", res);
}
return 0;
}








 本文介绍了一种计算包围一组树木所需的最短绳长的方法。利用凸包算法处理坐标点,适用于不超过100个坐标点的数据集。文章通过具体实例展示了如何通过编程实现该算法。
本文介绍了一种计算包围一组树木所需的最短绳长的方法。利用凸包算法处理坐标点,适用于不超过100个坐标点的数据集。文章通过具体实例展示了如何通过编程实现该算法。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








