1.6 LeetCode总结（线性表）_单调栈类

编程总结

每每刷完一道题后，其思想和精妙之处没有地方记录，本篇博客用以记录刷题过程中的遇到的算法和技巧
这类型的题目有一定的套路模板，需要持续刷，熟练掌握模板，详见单调递增栈的伪代码。
本文基础讲解部分，参考如下链接，基础知识需要了解清楚，才会写代码
参考链接1：https://blog.youkuaiyun.com/lucky52529/article/details/89155694
参考链接2：https://www.bilibili.com/video/BV1my4y1Z7jj/?spm_id_from=333.788&vd_source=69b69aec9479090b82c45d4b18beb481

单调栈的作用：找其左\右第一个比它大\小的元素, 记录之前遍历过的元素(top)

什么是单调栈？

从名字上就听的出来，单调栈中存放的数据应该是有序的，所以单调栈也分为单调递增栈和单调递减栈

单调递增栈：单调递增栈就是从栈底到栈顶数据是从大到小
单调递减栈：单调递减栈就是从栈底到栈顶数据是从小到大

递增栈 ：
pointer: top bottom
Index : 3 2 1 0
val: 10 20 20 60
-》》》》》》》》- 递增

举例：
现在有一组数10，3，7，4，12。

从左到右依次入栈，则如果栈为空或入栈元素值小于栈顶元素值，则入栈；否则，如果入栈则会破坏栈的单调性，则需要把比入栈元素小的元素全部出栈。单调递减的栈反之。

1）10入栈时，栈为空，直接入栈，栈内元素为 10
2）3入栈时， 栈顶元素10比3大，则入栈，栈内元素为 10，3
3）7入栈时， 栈顶元素3比7小，则栈顶元素出栈，此时栈顶元素为10，比7大，则7入栈，栈内元素为 10，7
4）4入栈时， 栈顶元素7比4大，则入栈，栈内元素为 10，7，4
5）12入栈时，栈顶元素4比12小，4出栈，此时栈顶元素为7，仍比12小，栈顶元素7继续出栈，此时栈顶元素为10，仍比12小，10出栈， 此时栈为空，12入栈，栈内元素为 12。

单调递增栈的伪代码

int stack[size];
//此处一般需要给数组最后添加结束标志符，具体下面例题会有详细讲解
for (遍历这个数组)
{
	if (栈空 || 栈顶元素大于等于当前比较元素)
	{
		入栈;
	} else
	{
		while (栈不为空 && 栈顶元素小于当前元素)
		{
			栈顶元素出栈;
			更新结果;
		}
		当前数据入栈;
	}
}

739. 每日温度

示例 1:
输入: temperatures = [73, 74, 75, 71, 69, 72, 76, 73]
输出: output = [1, 1, 4, 2, 1, 1, 0, 0]
index = [0, 1, 2, 3, 4, 5, 6, 7]

思路：裸的单调栈的题目

下面的方法与伪代码提供的框架一致, stack数组是用来记录下标的, temperatures[stack[top]] 为值
这里的 stack 是用来记录遍历过的元素的下标，因为题目是求下一个更高温度出现在几天后，是坐标相减
思路
首先想到的当然是暴力解法，两层for循环，把至少需要等待的天数就搜出来了。时间复杂度是O(n^2)

那么接下来在来看看使用单调栈的解法。
那有同学就问了，我怎么能想到用单调栈呢？ 什么时候用单调栈呢？

通常是一维数组，要寻找任一个元素的右边或者左边第一个比自己大或者小的元素的位置，此时我们就要想到可以用单调栈了。时间复杂度为O(n)。

例如本题其实就是找找到一个元素右边第一个比自己大的元素，此时就应该想到用单调栈了。

那么单调栈的原理是什么呢？为什么时间复杂度是O(n)就可以找到每一个元素的右边第一个比它大的元素位置呢？

单调栈的本质是空间换时间，因为在遍历的过程中需要用一个栈来记录右边第一个比当前元素高的元素，优点是整个数组只需要遍历一次。

更直白来说，就是用一个栈来记录我们遍历过的元素，因为我们遍历数组的时候，我们不知道之前都遍历了哪些元素，以至于遍历一个元素找不到是不是之前遍历过一个更小的，所以我们需要用一个容器（这里用单调栈）来记录我们遍历过的元素。

在使用单调栈的时候首先要明确如下几点：
单调栈里存放的元素是什么？
单调栈里只需要存放元素的下标i就可以了，如果需要使用对应的元素，直接T[i]就可以获取。

单调栈里元素是递增呢？ 还是递减呢？
注意以下讲解中，顺序的描述为 从栈头到栈底的顺序，因为单纯的说从左到右或者从前到后，不说栈头朝哪个方向的话，大家一定比较懵。

这里我们要使用递增循序（再强调一下是指从栈头到栈底的顺序），因为只有递增的时候，栈里要加入一个元素i的时候，才知道栈顶元素在数组中右面第一个比栈顶元素大的元素是i。

即：如果求一个元素右边第一个更大元素，单调栈就是递增的，如果求一个元素右边第一个更小元素，单调栈就是递减的。

文字描述理解起来有点费劲，接下来我画了一系列的图，来讲解单调栈的工作过程，大家再去思考，本题为什么是递增栈。

使用单调栈主要有三个判断条件。
当前遍历的元素T[i]小于栈顶元素T[st.top()]的情况
当前遍历的元素T[i]等于栈顶元素T[st.top()]的情况
当前遍历的元素T[i]大于栈顶元素T[st.top()]的情况
把这三种情况分析清楚了，也就理解透彻了。

// 递增栈，栈顶最小，栈底最大
struct Stack {
	int val;
	int idx;
};
void printStack(struct Stack *stack, int top)
{
	for (int i = 0; i < top; i++) {
		printf("stack[%d] = %d ", stack[i].idx, stack[i].val);
	}
	printf("\n");
}
// 递增栈，栈顶最小，栈底最大
int *dailyTemperatures(int* temperatures, int temperaturesSize, int* returnSize)
{
	int n = temperaturesSize;
	int *res   = (int *)malloc(sizeof(int) * n);
	// stack数组记录下标, temperatures[stack[top - 1]]为值
	struct Stack *stack = (struct Stack *)malloc(sizeof(struct Stack) * n);
	int top = 0;
	int index;
	memset(res,   0, sizeof(int) * n);
	memset(stack, 0, sizeof(struct Stack) * n);
	*returnSize = n;
	for (int i = 0; i < n; i++) {
		// 1.当前元素小于等于栈顶元素，则入栈
		if ((top == 0) || (temperatures[i] <= temperatures[stack[top - 1].idx])) {
			stack[top].idx = i;
			stack[top].val = temperatures[i];
			top++;
			printf("stack[%d]=%d in_stack: ", i, temperatures[i]);
			printStack(stack, top);
		} else {
			// 2.当前元素大于栈顶元素大，则找到了答案计算其下标
			// top > 0 代表栈不为空
			while ((top > 0) && (temperatures[i] > temperatures[stack[top - 1].idx])) {
				index = stack[top - 1].idx;
				res[index] = (i - index); // 结果数组
				printf("stack[%d]=%d out_stack:", i, temperatures[i]);
				printStack(stack, top);
				top--; // 出栈
			}
			stack[top].idx = i;
			stack[top].val = temperatures[i];
			top++;
			printf("stack[%d]=%d in_stack: ", i, temperatures[i]);
			printStack(stack, top);
		}
	}
	return res;
}

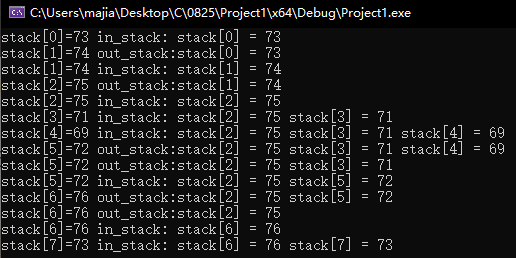
测试用例：int temperatures[8] = { 73, 74, 75, 71, 69, 72, 76, 73 }; 的进出函数调用栈如下图所示：
in_stack 代表进栈，out_stack 代表出栈

496. 下一个更大元素 I

思路：单调栈简单绕了一下，先求num2的单调栈，然后映射到num1即可

#define NUM_SIZE 10001
void GetNext(int *num, int size, int *res)
{
	int top = 0;
	int *stack = (int *)malloc(sizeof(int) * size);
	memset(stack, 0, sizeof(int) * size);
	for (int i = 0; i < size; i++) {
		if ((top == 0) || (num[i] <= stack[top - 1])) {
			stack[top] = num[i];
			top++;
		} else {
			while ((top > 0) && (num[i] > stack[top - 1])) { // 如果此时比较元素大于栈顶元素，则栈顶元素出栈.
				res[stack[top - 1]] = num[i];                 // 将找到的元素作为map存下来.
				top--;
			}
			stack[top] = num[i];
			top++;
		}
	}
	// 处理此时还未出栈的元素，都是不存在下一个更大元素的，赋值为-1。
	while (top > 0) {
		res[stack[top - 1]] = -1;
		top--;
	}
	free(stack);
}
int *nextGreaterElement(int *nums1, int nums1Size, int *nums2, int nums2Size, int *returnSize)
{
	int *ret = (int*)malloc(sizeof(int) * nums1Size);
	int *res = (int*)malloc(sizeof(int) * NUM_SIZE);  // hash map
	memset(ret, 0, sizeof(int) * nums1Size);
	memset(res, 0, sizeof(int) * NUM_SIZE);
	// 1. nums2求解右边第一个更大的元素.
	GetNext(nums2, nums2Size, res);
	// 2. nums1作为查询的行为，查找hash_map即可. 
	for (int i = 0; i < nums1Size; i++) {
		ret[i] = res[nums1[i]];
	}
	*returnSize = nums1Size;
	free(res);
	return ret;
}

503. 下一个更大元素Ⅱ

给定一个循环数组 nums （ nums[nums.length - 1] 的下一个元素是 nums[0] ），返回 nums 中每个元素的 下一个更大元素 。
数字 x 的 下一个更大的元素 是按数组遍历顺序，这个数字之后的第一个比它更大的数，这意味着你应该循环地搜索它的下一个更大的数。如果不存在，则输出 -1 。

示例 1:
输入: nums = [1,2,1]
输出: [2,-1,2]
解释: 第一个 1 的下一个更大的数是 2；
数字 2 找不到下一个更大的数；
第二个 1 的下一个最大的数需要循环搜索，结果也是 2。
示例 2：
输入: nums = [1,2,3,4,3]
输出: [2,3,4,-1,4]
提示:
1 <= nums.length <= 10^4
-10^9 <= nums[i] <= 10^9

思路：单调栈裸题，只是多了循环数组处理

手法1：循环数组的处理：a.数组下标两倍，b.下标 i % numsSize

int *nextGreaterElements(int *nums, int numsSize, int *returnSize)
{
    *returnSize = numsSize;
    if (numsSize == 0) {
        return NULL;
    }
    int *ret = malloc(sizeof(int) * numsSize);
    memset(ret, -1, sizeof(int) * numsSize);
    int stack[numsSize * 2 - 1];
    int top = 0;
    for (int i = 0; i < (numsSize * 2 - 1); i++) {
        while (top > 0 && nums[stack[top - 1]] < nums[i % numsSize]) {
            ret[stack[top - 1]] = nums[i % numsSize];
            top--;
        }
        stack[top++] = i % numsSize;
    }
    return ret;
}

42.接雨水

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。
示例 1：

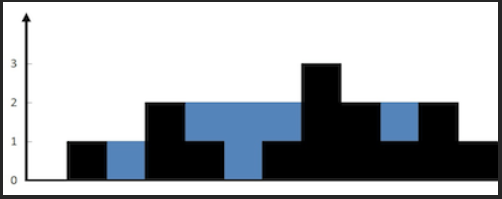
输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出：6
解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。
示例 2：
输入：height = [4,2,0,3,2,5]
输出：9

维护一个单调栈，单调栈存储的是下标，满足从栈底到栈顶的下标对应的数组 height 中的元素递减。
从左到右遍历数组，遍历到下标 i 时，如果栈内至少有两个元素，记栈顶元素为 top，top 的下面一个元素是 left，则一定有 height[left]≥height[top]。

1.如果 height[i] > height[top]，则得到一个可以接雨水的区域，该区域的宽度是 i−left−1，高度是 min(height[left], height[i]) − height[top]，根据宽度和高度即可计算得到该区域能接的雨水量。

2.为了得到 left，需要将 top 出栈。在对 top 计算能接的雨水量之后，left 变成新的 top，重复上述操作，直到栈变为空，或者栈顶下标对应的 height 中的元素大于或等于 height[i]。

3.在对下标 i 处计算能接的雨水量之后，将 i 入栈，继续遍历后面的下标，计算能接的雨水量。遍历结束之后即可得到能接的雨水总量

思路1：求当前元素右边第一个比它大的元素–单调栈

int trap(int *height, int heightSize)
{
    int n = heightSize;
    if (n == 0) {
        return 0;
    }
    int ans = 0;
    int stack[n], top = 0;
    for (int i = 0; i < n; ++i) {
        while ((top != 0) && (height[i] > height[stack[top - 1]])) {
            int stk_top = stack[top - 1];
            top--;
            if (top == 0) {
                break;
            }
            int left = stack[top - 1];
            int currWidth = i - left - 1;
            int currHeight = fmin(height[left], height[i]) - height[stk_top];
            ans += currWidth * currHeight;
        }
        stack[top++] = i;
    }
    return ans;
}