[ 算法 ] -- 归并排序，Java实现

归并排序基本思想：

归并排序是建立在归并操作上的一种有效的排序算法，采用“分治”思想。

归并排序将已经有序的子序列合并成一个序列，得到的序列完全有序；

二路归并：将两个有序表合成一个有序表

归并排序的特点：

时间复杂度：O(n*logn)
空间复杂度：O(n)
稳定性：稳定

归并排序的步骤：

1. 分解：将待排序的序列平均分解成两个元素个数相同的子序列；

2. 合并：合并两个有序的子序列，得到排序结果。

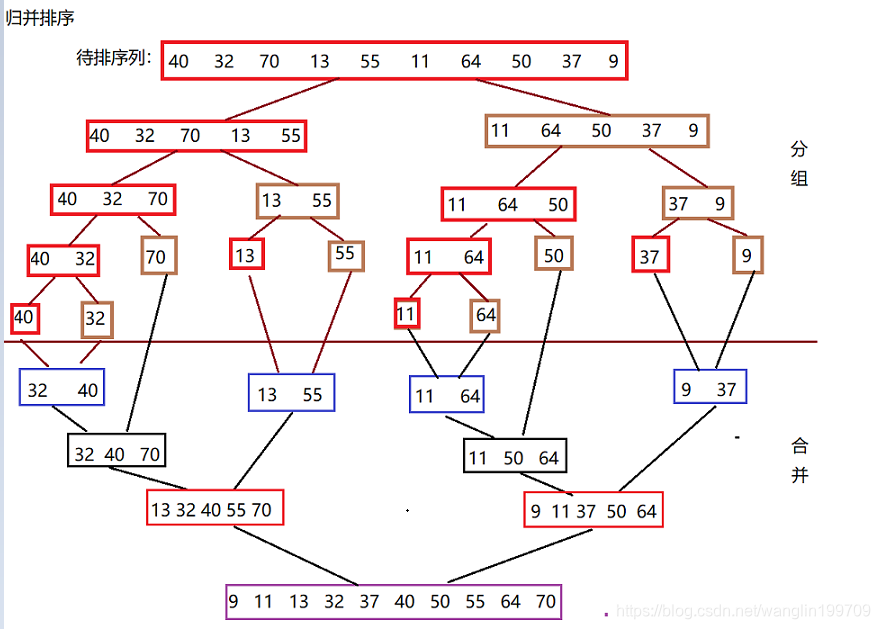
递归方法实现：

import java.util.Arrays;

public class MergeSort {
    //合并
    public static void merge(int[] arr, int start, int mid, int end,int[] tmpArray){
        int i = start;
        int tmpIndex = start;//新建数组的下标
        int s2 = mid + 1;
        //当有两个归并段时，且两个归并段都有数据
        while (start <= mid && s2 <= end){
            if (arr[start] <= arr[s2]){
                tmpArray[tmpIndex++] = arr[start++];
            }else {
                tmpArray[tmpIndex++] = arr[s2++];
            }
        }
        //证明第一个归并段有数据
        while (start <= mid){
            tmpArray[tmpIndex++] = arr[start++];
        }
        //证明第二个归并段有数据
        while (s2 <= end){
            tmpArray[tmpIndex++] = arr[s2++];
        }
        //将排好序的数据从tmpArray里边拷贝到arr
        while (i <= end){
            arr[i] = tmpArray[i];
            i++;
        }
    }

    private static void mergeSort(int[] arr, int start, int end,int[] tmpArray) {
        //分组的终止条件
        if (start >= end){
            return;
        }
        int mid = (start + end)/2;
        //右边
        mergeSort(arr, start, mid,tmpArray);
        //左边
        mergeSort(arr, mid + 1, end,tmpArray);
        //合并
        merge(arr,start,mid,end,tmpArray);
    }

    public static void main(String[] args) {
        int[] arr = {7,12,4,20,1,10,2};
        int[] tmpArray = new int[arr.length];
        System.out.println("排序之前："+Arrays.toString(arr));
        System.out.println();
        mergeSort(arr,0,arr.length - 1,tmpArray);
        System.out.println("排序之后："+Arrays.toString(arr));
    }
}

非递归方法实现：

import java.util.Arrays;

public class MergeSort1 {
    public static void main(String[] args) {
        int[] arr = {40,32,70,13,55,11,64,50,37,9};
        System.out.println("排序之前："+Arrays.toString(arr));
        System.out.println();
        mergeSort(arr);
        System.out.println("排序之后："+Arrays.toString(arr));
    }

    //mergeSort进行分组
    private static void mergeSort(int[] arr) {
        for (int i = 1; i < arr.length; i *= 2) {
            merge(arr,i);
        }
    }

    //gap表示一组里边有多少个数据
    //merge进行归并
    private static void merge(int[] arr, int gap) {
        int[] tmpArray = new int[arr.length];
        int i = 0;//tmpArray的下标
        int start1 = 0;//第一个数组开始
        int end1 = start1 + gap -1;//第一个数组结束
        int start2 = end1 + 1;//第二个数组开始
        int end2 = start2+gap-1 <= arr.length-1 ? start2+gap-1 : arr.length-1; //第二个数组结束
        //保证有两个归并段
        while (start2 < arr.length){
            //保证两个归并段都有数据
            while (start1 <= end1 && start2 <= end2){
                //开始比较
                if (arr[start1] <= arr[start2]){
                    tmpArray[i++] = arr[start1++];
                }else {
                    tmpArray[i++] = arr[start2++];
                }
            }
            while (start1 <= end1){
                tmpArray[i++] = arr[start1++];
            }
            while (start2 <= end2){
                tmpArray[i++] = arr[start2++];
            }
            start1 = end2+1;//第一个数组开始
            end1 = start1 + gap -1;//第一个数组结束
            start2 = end1 + 1;//第二个数组开始
            end2 = start2+gap-1 <= arr.length-1 ? start2+gap-1 : arr.length-1; //第二个数组结束

        }
        while (start1 < arr.length){

            tmpArray[i++] = arr[start1++];
        }
        //拷贝数据到原始数组
        for (int j = 0; j < tmpArray.length; j++) {
            arr[j] = tmpArray[j];
        }
    }
}