LeetCode每日一题(1627. Graph Connectivity With Threshold)

给定n个城市，城市间存在由共同最大公约数决定的双向道路。若两个城市的数字x和y有大于阈值z的公约数，则它们直接相连。根据n和threshold以及一组查询，判断每对城市ai和bi之间是否存在路径。返回一个布尔数组，表示每个查询的答案。

We have n cities labeled from 1 to n. Two different cities with labels x and y are directly connected by a bidirectional road if and only if x and y share a common divisor strictly greater than some threshold. More formally, cities with labels x and y have a road between them if there exists an integer z such that all of the following are true:

x % z == 0,
y % z == 0, and
z > threshold.

Given the two integers, n and threshold, and an array of queries, you must determine for each queries[i] = [ai, bi] if cities ai and bi are connected directly or indirectly. (i.e. there is some path between them).

Return an array answer, where answer.length == queries.length and answer[i] is true if for the ith query, there is a path between ai and bi, or answer[i] is false if there is no path.

Example 1:

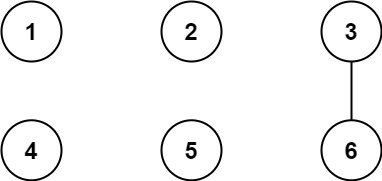
Input: n = 6, threshold = 2, queries = [[1,4],[2,5],[3,6]]
Output: [false,false,true]

Explanation: The divisors for each number:
1: 1
2: 1, 2
3: 1, 3
4: 1, 2, 4
5: 1, 5
6: 1, 2, 3, 6
Using the underlined divisors above the threshold, only cities 3 and 6 share a common divisor, so they are the
only ones directly connected. The result of each query:
[1,4] 1 is not connected to 4
[2,5] 2 is not connected to 5
[3,6] 3 is connected to 6 through path 3–6

Example 2:

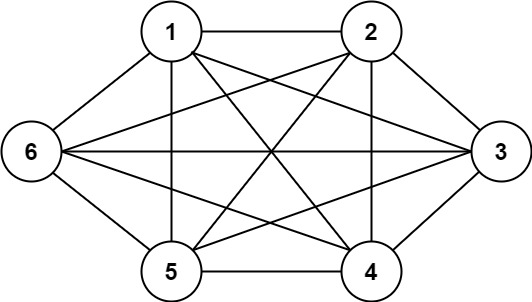
Input: n = 6, threshold = 0, queries = [[4,5],[3,4],[3,2],[2,6],[1,3]]
Output: [true,true,true,true,true]

Explanation: The divisors for each number are the same as the previous example. However, since the threshold is 0,
all divisors can be used. Since all numbers share 1 as a divisor, all cities are connected.

Example 3:

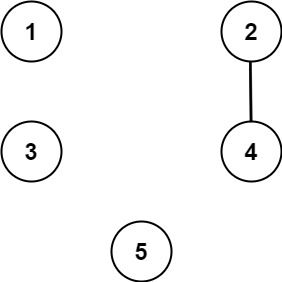
Input: n = 5, threshold = 1, queries = [[4,5],[4,5],[3,2],[2,3],[3,4]]
Output: [false,false,false,false,false]

Explanation: Only cities 2 and 4 share a common divisor 2 which is strictly greater than the threshold 1, so they are the only ones directly connected.
Please notice that there can be multiple queries for the same pair of nodes [x, y], and that the query [x, y] is equivalent to the query [y, x].

Constraints:

2 <= n <= 104
0 <= threshold <= n
1 <= queries.length <= 105
queries[i].length == 2
1 <= ai, bi <= cities
ai != bi

题目没有想象中的复杂，就是个最基本的 union find, 有共同的 divsor 的数字在同一个 disjoint set 中，查询的时候检查要查询的两个数是不是在同一个 disjoint set 中就可以了


impl Solution {
    fn find(parents: &mut [usize], i: usize) -> usize {
        if parents[i] == i {
            return i;
        }
        let p = Solution::find(parents, parents[i]);
        parents[i] = p;
        p
    }

    fn union(parents: &mut [usize], i: usize, j: usize) {
        let pi = Solution::find(parents, i);
        let pj = Solution::find(parents, j);
        if pi != pj {
            parents[pi] = pj;
        }
    }
    pub fn are_connected(n: i32, threshold: i32, queries: Vec<Vec<i32>>) -> Vec<bool> {
        let mut parents: Vec<usize> = (0usize..=n as usize).into_iter().collect();
        for i in threshold + 1..=n {
            let mut m = 1;
            while i * m <= n {
                Solution::union(&mut parents, i as usize, (i * m) as usize);
                m += 1;
            }
        }
        for i in 0..parents.len() {
            Solution::find(&mut parents, i);
        }
        let mut ans = vec![false; queries.len()];
        for (i, query) in queries.into_iter().enumerate() {
            let p1 = Solution::find(&mut parents, query[0] as usize);
            let p2 = Solution::find(&mut parents, query[1] as usize);
            ans[i] = p1 == p2;
        }
        ans
    }
}