LeetCode每日一题(2014. Longest Subsequence Repeated k Times)

You are given a string s of length n, and an integer k. You are tasked to find the longest subsequence repeated k times in string s.

A subsequence is a string that can be derived from another string by deleting some or no characters without changing the order of the remaining characters.

A subsequence seq is repeated k times in the string s if seq _ k is a subsequence of s, where seq _ k represents a string constructed by concatenating seq k times.

For example, “bba” is repeated 2 times in the string “bababcba”, because the string “bbabba”, constructed by concatenating “bba” 2 times, is a subsequence of the string “bababcba”.
Return the longest subsequence repeated k times in string s. If multiple such subsequences are found, return the lexicographically largest one. If there is no such subsequence, return an empty string.

Example 1:

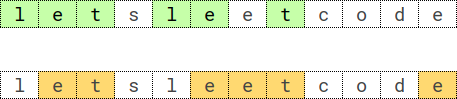
Input: s = “letsleetcode”, k = 2
Output: “let”

Explanation: There are two longest subsequences repeated 2 times: “let” and “ete”.
“let” is the lexicographically largest one.

Example 2:

Input: s = “bb”, k = 2
Output: “b”

Explanation: The longest subsequence repeated 2 times is “b”.

Example 3:

Input: s = “ab”, k = 2
Output: “”
Explanation: There is no subsequence repeated 2 times. Empty string is returned.

Constraints:

• n == s.length
• 2 <= n, k <= 2000
• 2 <= n < k * 8
• s consists of lowercase English letters.

---

限制条件中的 2 <= n < k * 8 是这题的关键， 两边同时除以 k 得到 n/k < 8, 也就是我们最终答案的长度不会超过 8。我们首先对 s 中的 char 进行 freq 计数， 只有 freq/k > 0 的 char 才可能出现在答案中。我们将这些 char 和对应的 freq 收集起来， 然后从 length = n / k 开始，以字母顺序倒序排列这些 char， 组成长度为 length 的字符串， 然后检验这些字符串是不是在 s 中出现 k 次，如果符合直接返回， 因为我们的 length 是递减的， 并且我们是按字母顺序倒序来组合的。

---

impl Solution {
    fn is_match(origin: &[char], target: &[char]) -> bool {
        let mut oi = 0;
        let mut ti = 0;
        while oi < origin.len() {
            if origin[oi] != target[ti] {
                oi += 1;
                continue;
            }
            if ti == target.len() - 1 {
                return true;
            }
            ti += 1;
            oi += 1;
        }
        false
    }

    fn match_permutation(counts: &mut Vec<(char, i32)>, target: &mut Vec<char>, indices: &mut Vec<usize>, k: usize, i: usize, origin: &[char]) -> Option<String> {
        if i == target.len() {
            if Solution::is_match(origin, &target.repeat(k)) {
                return Some(target.into_iter().map(|c| *c).collect());
            }
            return None;
        }
        let counts_length = counts.len();
        for _ in 0..counts_length {
            if counts[indices[i]].1 == 0 {
                indices[i] += 1;
                indices[i] %= counts_length;
                continue;
            }
            counts[indices[i]].1 -= 1;
            target[i] = counts[indices[i]].0;
            if let Some(ans) = Solution::match_permutation(counts, target, indices, k, i + 1, origin) {
                return Some(ans);
            }
            counts[indices[i]].1 += 1;
            indices[i] += 1;
            indices[i] %= counts_length;
        }
        None
    }

    pub fn longest_subsequence_repeated_k(s: String, k: i32) -> String {
        let counts = s.chars().fold(vec![0; 26], |mut l, c| {
            l[c as usize - 97] += 1;
            l
        });
        let mut max_length = 0;
        let mut counts: Vec<(char, i32)> = counts
            .into_iter()
            .enumerate()
            .filter(|&(_, n)| n / k > 0)
            .map(|(i, n)| {
                max_length += n / k;
                ((i + 97) as u8 as char, n / k)
            })
            .collect();
        counts.reverse();
        let origin: Vec<char> = s.chars().collect();
        for l in (1..=max_length).rev() {
            if let Some(ans) = Solution::match_permutation(&mut counts, &mut vec!['-'; l as usize], &mut vec![0; l as usize], k as usize, 0, &origin) {
                return ans;
            }
        }
        "".into()
    }
}