LeetCode每日一题(2368. Reachable Nodes With Restrictions)

There is an undirected tree with n nodes labeled from 0 to n - 1 and n - 1 edges.

You are given a 2D integer array edges of length n - 1 where edges[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the tree. You are also given an integer array restricted which represents restricted nodes.

Return the maximum number of nodes you can reach from node 0 without visiting a restricted node.

Note that node 0 will not be a restricted node.

Example 1:

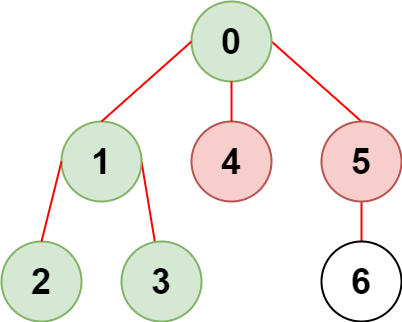
Input: n = 7, edges = [[0,1],[1,2],[3,1],[4,0],[0,5],[5,6]], restricted = [4,5]
Output: 4

Explanation:
The diagram above shows the tree.
We have that [0,1,2,3] are the only nodes that can be reached from node 0 without visiting a restricted node.

Example 2:

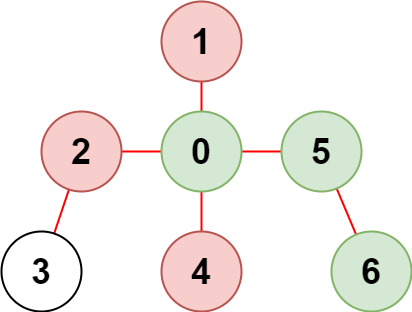
Input: n = 7, edges = [[0,1],[0,2],[0,5],[0,4],[3,2],[6,5]], restricted = [4,2,1]
Output: 3

Explanation:
The diagram above shows the tree.
We have that [0,5,6] are the only nodes that can be reached from node 0 without visiting a restricted node.

Constraints:

• 2 <= n <= 105
• edges.length == n - 1
• edges[i].length == 2
• 0 <= ai, bi < n
• ai != bi
• edges represents a valid tree.
• 1 <= restricted.length < n
• 1 <= restricted[i] < n
• All the values of restricted are unique.

---

既然说是一棵树了， 那我们就把 0 作为 root，dfs 向下遍历整棵树就好了， 实现写的有些麻烦了， 因为这是棵树，所以任意两个 node 之间一定是只有唯一一条 edge 的， 所以检查的时候不需要 visited，只需要检查上一个 node 就可以了。

---

use std::collections::{HashMap, HashSet};

impl Solution {
    fn dfs(
        n: i32,
        edges: &HashMap<i32, Vec<i32>>,
        restricted: &HashSet<i32>,
        visited: &mut HashSet<i32>,
        ans: &mut i32,
    ) {
        if restricted.contains(&n) || visited.contains(&n) {
            return;
        }
        visited.insert(n);
        *ans += 1;
        for &e in edges.get(&n).unwrap() {
            Solution::dfs(e, edges, restricted, visited, ans);
        }
    }
    pub fn reachable_nodes(n: i32, edges: Vec<Vec<i32>>, restricted: Vec<i32>) -> i32 {
        let edges = edges.into_iter().fold(HashMap::new(), |mut m, v| {
            m.entry(v[0]).or_insert(Vec::new()).push(v[1]);
            m.entry(v[1]).or_insert(Vec::new()).push(v[0]);
            m
        });
        let mut ans = 0;
        Solution::dfs(
            0,
            &edges,
            &restricted.into_iter().collect(),
            &mut HashSet::new(),
            &mut ans,
        );
        ans
    }
}