LeetCode每日一题(1457. Pseudo-Palindromic Paths in a Binary Tree)

Given a binary tree where node values are digits from 1 to 9. A path in the binary tree is said to be pseudo-palindromic if at least one permutation of the node values in the path is a palindrome.

Return the number of pseudo-palindromic paths going from the root node to leaf nodes.

Example 1:

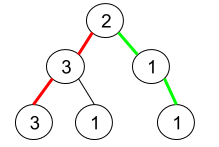
Input: root = [2,3,1,3,1,null,1]
Output: 2

Explanation: The figure above represents the given binary tree. There are three paths going from the root node to leaf nodes: the red path [2,3,3], the green path [2,1,1], and the path [2,3,1]. Among these paths only red path and green path are pseudo-palindromic paths since the red path [2,3,3] can be rearranged in [3,2,3] (palindrome) and the green path [2,1,1] can be rearranged in [1,2,1] (palindrome).

Example 2:

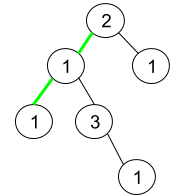
Input: root = [2,1,1,1,3,null,null,null,null,null,1]
Output: 1

Explanation: The figure above represents the given binary tree. There are three paths going from the root node to leaf nodes: the green path [2,1,1], the path [2,1,3,1], and the path [2,1]. Among these paths only the green path is pseudo-palindromic since [2,1,1] can be rearranged in [1,2,1] (palindrome).

Example 3:

Input: root = [9]
Output: 1

Constraints:

• The number of nodes in the tree is in the range [1, 105].
• 1 <= Node.val <= 9

---

既然是任意组合能形成回文就可以，那其实就是只对数量有限制，对位置没限制， 形成回文对数量的限制无非就是奇数数量的字符最多只能有 1 个， 其他字符都必须是偶数个， 就这道题而言， 我们只需要维护对每一个数字的计数， 同时维护这些计数里面奇数数量的个数就可以了， 只要这个奇数计数<=1， 那就可以认定当前路径是可以形成回文的。

---

use std::cell::RefCell;
use std::rc::Rc;
impl Solution {
    fn rc(
        root: Option<Rc<RefCell<TreeNode>>>,
        mut odd_count: i32,
        mut counts: Vec<i32>,
        ans: &mut i32,
    ) {
        if let Some(node) = root {
            let val = node.borrow().val;
            counts[val as usize - 1] += 1;
            if counts[val as usize - 1] % 2 == 1 {
                odd_count += 1;
            } else {
                odd_count -= 1;
            }
            if node.borrow().left.is_none() && node.borrow().right.is_none() {
                if odd_count == 0 || odd_count == 1 {
                    *ans += 1;
                }
                return;
            }
            Solution::rc(
                node.borrow_mut().left.take(),
                odd_count,
                counts.clone(),
                ans,
            );
            Solution::rc(
                node.borrow_mut().right.take(),
                odd_count,
                counts.clone(),
                ans,
            );
        }
    }
    pub fn pseudo_palindromic_paths(root: Option<Rc<RefCell<TreeNode>>>) -> i32 {
        let mut ans = 0;
        Solution::rc(root, 0, vec![0; 9], &mut ans);
        ans
    }
}