从研究生时期就接触了神经网络算法,其中的反向传播BP算法是目前应用神经网络算法里使用最为广泛的算法,包括最近非常火爆的深度学习算法中都用到了这个算法。但是一直以来,自己对BP算法都没有做过仔细的数学推导,只是做到大概了解原理,不能深刻记忆,每次再看的时候又需要重新理解一遍。

推导过程遇到的几个问题
1. 不同的Cost函数。开始的时候看到的网上有贴出来Ufldl里面的BP推导过程,虽然都是Ng的课程,但是这两个课程里面BP算法用到的Cost函数不一样
Ufldl课程里的Cost函数,用了最常规的最小二乘法代价函数
上面第二个J函数参数变量θ等价于第一个的W,b,但是上面两个函数形式完全不一样,网上的很多推导都是基于第一个Cost函数的形式,而实际上BP算法的cost函数是可以不同的,不利于对整个过程的理解,因此推导过程应该是基于函数范式而不是特定的函数表达式;
2. 链式法则。其实BP算法推导最主要用到的就是微积分里的偏导数链式法则,虽然数学系毕业,基本上也忘得也差不多,索性把找到的证明过程也贴出来,有兴趣的同学可以看一下
链式法则:
一元复合的情况

多元复合的情况
考虑函数z
对一元复合情况的证明:
设f和g为函数,x为常数,使得f在g(x)可导,且g在x可导。根据可导的定义,
-
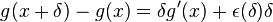 ,其中当
,其中当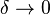 时,
时, 。
。
同理,
-
 ,其中当
,其中当 时,
时, 。
。
现在
其中 . 注意到当
. 注意到当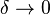 时,
时, 及
及 ,因此
,因此  。因此
。因此
下面正式进入推导过程
其实BP算法推导的关键点就是找到层之间的传递关系,即
第一步、先定义变量




























 1187
1187

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








