二叉树

1. 树（Tree）的基本概念

       树(Tree)是n(n≧0)个结点的有限集。在任意一颗非空树中：有且仅有一个特定的称为根的结点。n=0时称为空树。

       n=0时称为空树。

       n>1时，其余结点可分为m(m>0)个互不相交的有限集T1，T2，T3，……，Tm，其中每个集合本身又是一棵树，并且称为根的子树。

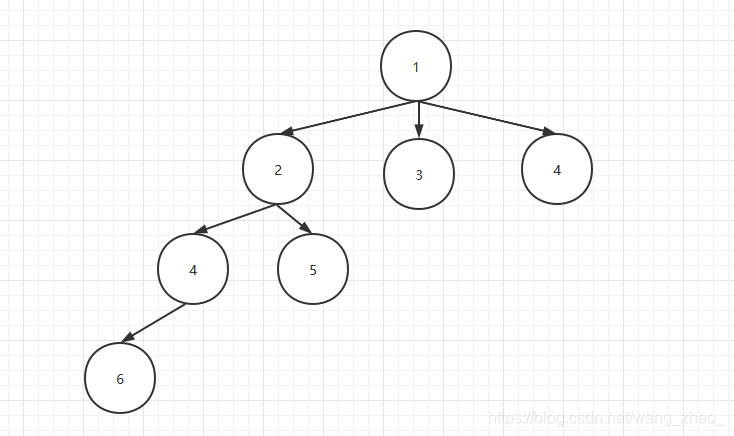
• 节点：树中的每一个元素都是一个节点，如上图中1，2，3，4，5，6等都是树的节点，节点可以为NULL，上图中并未直接画出。

• 根节点：一棵树中有且仅有一个根节点，上图中1为根节点。

• 父节点：上图中1是2、3、4的父节点，2是4和5的父节点…。

• 子节点：上图中2、3和4分别是1的子节点…。

• 兄弟节点：父节点的子节点被称为兄弟节点，如4和5之间为兄弟节点。

• 节点的度（degree）：子树的个数，如节点1的度为3，节点2的度为2。

• 树的度（degree）：所有节点度中最大的值。

• 叶子节点（leaf）：度为 0 的节点。

• 非叶子节点：度不为0的节点。

• 层数：根节点在第一层，根节点的子节点在第二层，以此类推。

• 节点的深度（depth）：从根节点到当前节点的唯一路径的节点总数，如节点4的深度为3。

• 节点的高度（height）：从当前节点到最远叶子节点的路径上的节点总数，如节点4的高度为2。

• 树的深度：所有节点深度中的最大值。

• 树的高度：所有节点高度中的最大值。

• 树的深度等于树的高度。

2. 有序树、无序树和森林

• 有序树

       树中任意节点的子节点之间有顺序关系

• 无序树

       树中任意节点的子节点之间没有顺序关系

       也称为”自由树”

• 森林

       由m (m≥0)棵互不相交的树组成的集合

3. 二叉树

• 二叉树的特点

       每个节点的度最大为2 （最多拥有2棵子树）。

       左子树和右子树是有顺序的。

       即使某节点只有一棵子树，也要区分左右子树。

• 二叉树是有序树还是无序树？

       有序树

4. 二叉树的性质

1. 非空二叉树的第i层最多有2^(i-1)个节点。
2. 在高度为h的二叉树上最多有2^h - 1个结点（h≥1）
3. 对于任何一棵非空二叉树，如果叶子节点个数为n0，度为2的节点个数为n2，则有：n0 = n2 + 1。

       假设度为1的节点的个数为n1，则有no + n1 + n2 = n，n为节点的个数。当节点个数为n时，则二叉树中边的个数为n-1。当度为2的节点个数为n2，则存在的边数为2 * n2，当度为1的节点个数为n1，则存在的边数为n1，当度为0的节点个数为n0，则存在的边数为0，可得2 * n2 + n1 = n - 1。

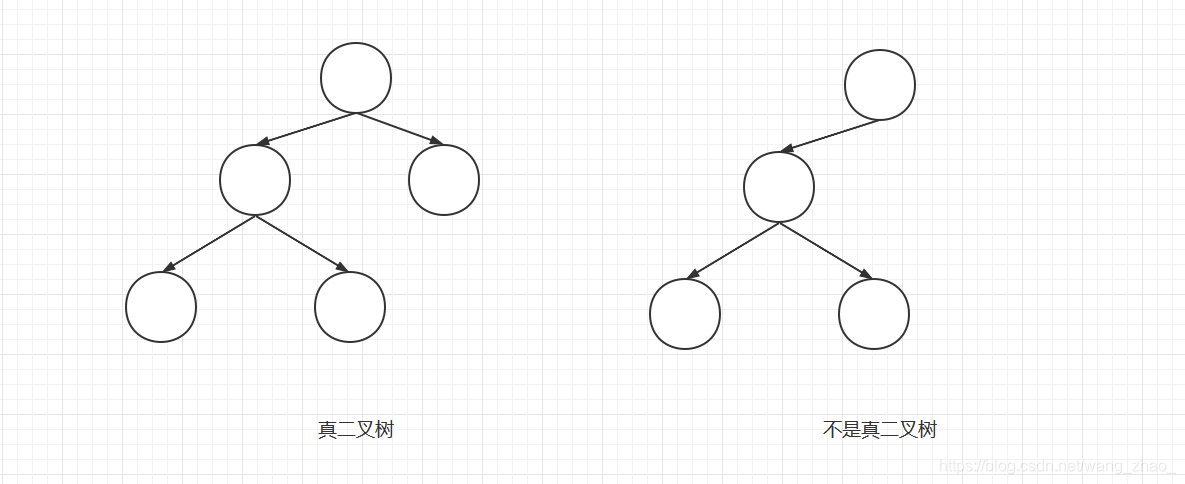
5. 真二叉树

• 真二叉树：所有节点的度都要么为0，要么为2。

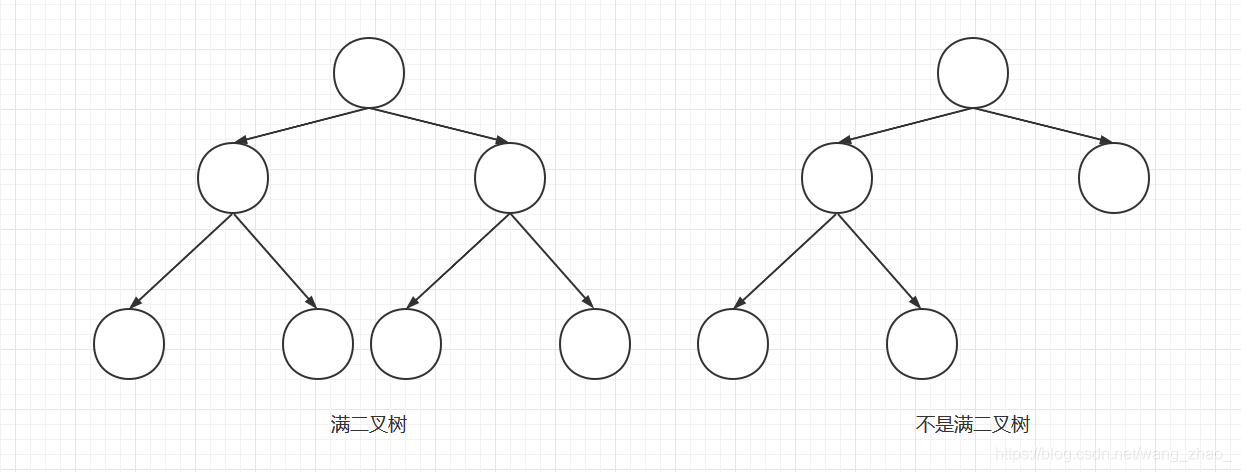
6. 满二叉树

• 满二叉树：一个二叉树，如果每一个层的结点数都达到最大值，则这个二叉树就是满二叉树。

• 在同样高度的二叉树中，满二叉树的叶子节点数量最多、总节点数量最多。

• 满二叉树一定是真二叉树，真二叉树不一定是满二叉树。

• 假设满二叉树的高度为h （h≥1），那么

       第i层的节点数量:2^(i-1)。

       叶子节点数量: 2^(h-1)。

       总节点的数量n，n = 2 ^ h- 1 = 2 ^ 0 + 2 ^ 1 + ...... + 2 ^ (h-1)，则h = log(n + 1)。

7. 完全二叉树

• 完全二叉树：叶子节点只会出现最后2层，且最后1层的叶子结点都靠左对齐。

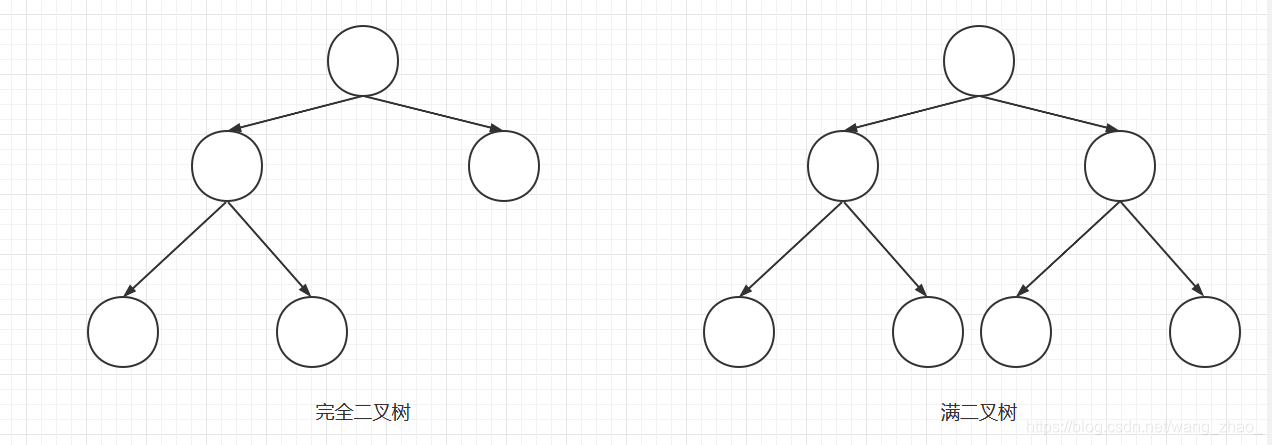
• 完全二叉树从根结点至倒数第2层是一棵满二叉树
• 满二叉树一定是完全二叉树，完全二叉树不一定是满二叉树

8. 完全二叉树的性质

• 度为1的节点只有左子树。

• 度为1的节点要么是1个，要么是0个。

• 同样节点数量的二叉树，完全二叉树的高度最小。

• 假设完全二叉树的高度为h(h≥1)，那么

  • 至少有2^(h-1)个节点( 2^0 + 2^1 +2^2 + ... + 2^(h-2) +1)

  • 最多有2^h - 1个节点(2^0 + 2^1 + 2^2 + ... + 2^(h-1)， 满二叉树)

  • 总节点数量为n

    • 2^(h-1) <= n < 2^h
    • h - 1 <= log(n) < h
    • h = floor(log(n)) + 1

• 一棵有n个节点的完全二叉树(n>0)，从上到下、从左到右对节点从0开始进行编号,对任意第i个节点。

  • 如果i = 0,它是根节点。
  • 如果i > 0，它的父节点编号为floor(i-1)/2)。
  • 如果2i + 1 ≤ n -1,它的左子节点编号为2i + 1。
  • 如果2i + 1 > n-1，它无左子节点。
  • 如果2i + 2 ≤ n-1，它的右子节点编号为2i+ 2。
  • 如果2i + 2 > n-1，它无右子节点。

测试题

       如果一棵完全二叉树有768个节点，求叶子节点的个数？

       假设叶子节点个数为n0，度为1的节点个数为n1，度为2的节点个数为n2。

       总结点个数n = n0 + n1 + n2，而且n0 = n2 + 1，所以有n = 2 * n0 + n1 - 1。

       完全二叉树的n1要么为0，要么为1

       n1为1时，n = 2 * n0，n必然是偶数：

              叶子节点个数n0 = n / 2，非叶子节点个数n1 + n2= n/2。

       n1为0时，n = 2 * n0 - 1，n必然是奇数：
              叶子节点个数n0 = (n + 1)/ 2，非叶子节点个数n1 + n2 = (n- 1)/2。

9. 构建二叉树

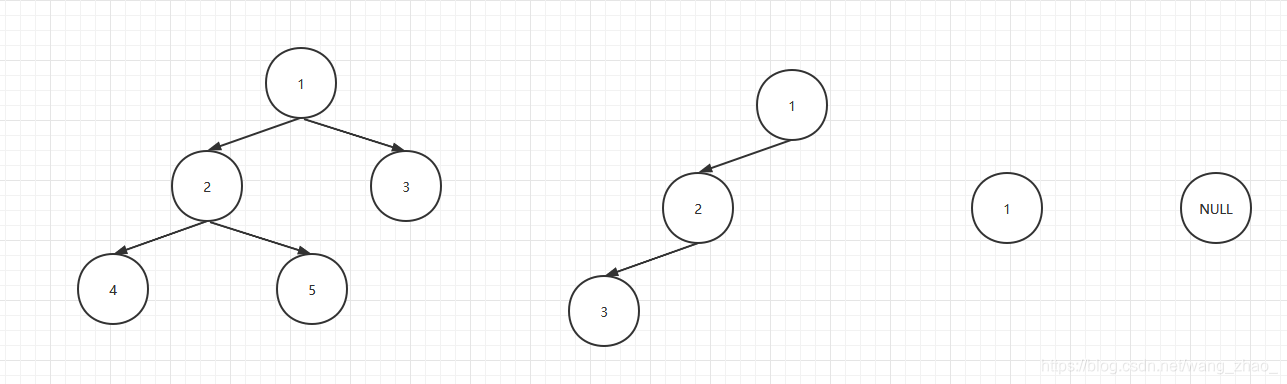
       倘若，我们想要构建下图所示的一棵二叉树，应该如何构建呢？

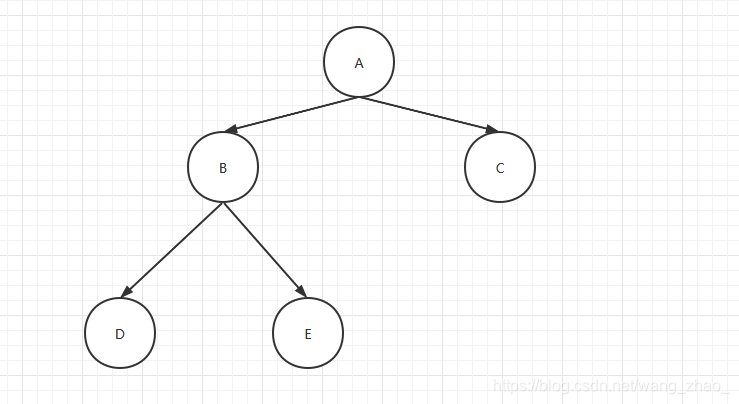
       采用递归的方式，首先可以构建根节点，然后构建根节点的左子树，接着构建根节点右子树。
       既然采用递归，那么一定得有递归的终止条件，那么何时终止呢？答案便是节点为NULL的时候，这里我们以#字符代替空节点。

       接下来，便进入代码的研究。

       首先，我们可以看一下，二叉树节点的定义。

/**
 * @author wangzhao
 * @date 2020/7/1 2:11
 */
public class TreeNode<E> {
   
   

    public E value;
    public TreeNode<E> left;
    public TreeNode<E> right;
    public TreeNode<E> parent;

    public TreeNode(E value, TreeNode<E> parent) {
   
   
        this.value = value;
        this.parent = parent;
    }
}

       相比于前面介绍的二叉树，多了一个parent指针，不过这并不影响我们对二叉树的使用，这样定义是为了后面其他树的学习。

       二叉树的构建代码可以看createTree()方法。

import	java.util.Scanner;
import	java.util.Scanner;/**
 * @author wangzhao
 * @date 2020/7/1 2:10
 */
public class BinaryTree {
   
   

    private TreeNode root;

    public TreeNode createTree(){
   
   
        root = createTree(null);
        return root;
    }

    private TreeNode createTree(TreeNode parentNode){
   
   
        Scanner input = new Scanner(System.in);
        char ch = input.next().charAt(0);
        // 递归的终止条件
        if (ch == '#'){
   
   
            return null;
        }
        // 首先构建根节点
        TreeNode node = new TreeNode(ch, parentNode);
        // 接着构建根节点的左子树
        node.left = createTree(node