力扣2829题解

学习记录

2025.3.26

题目：

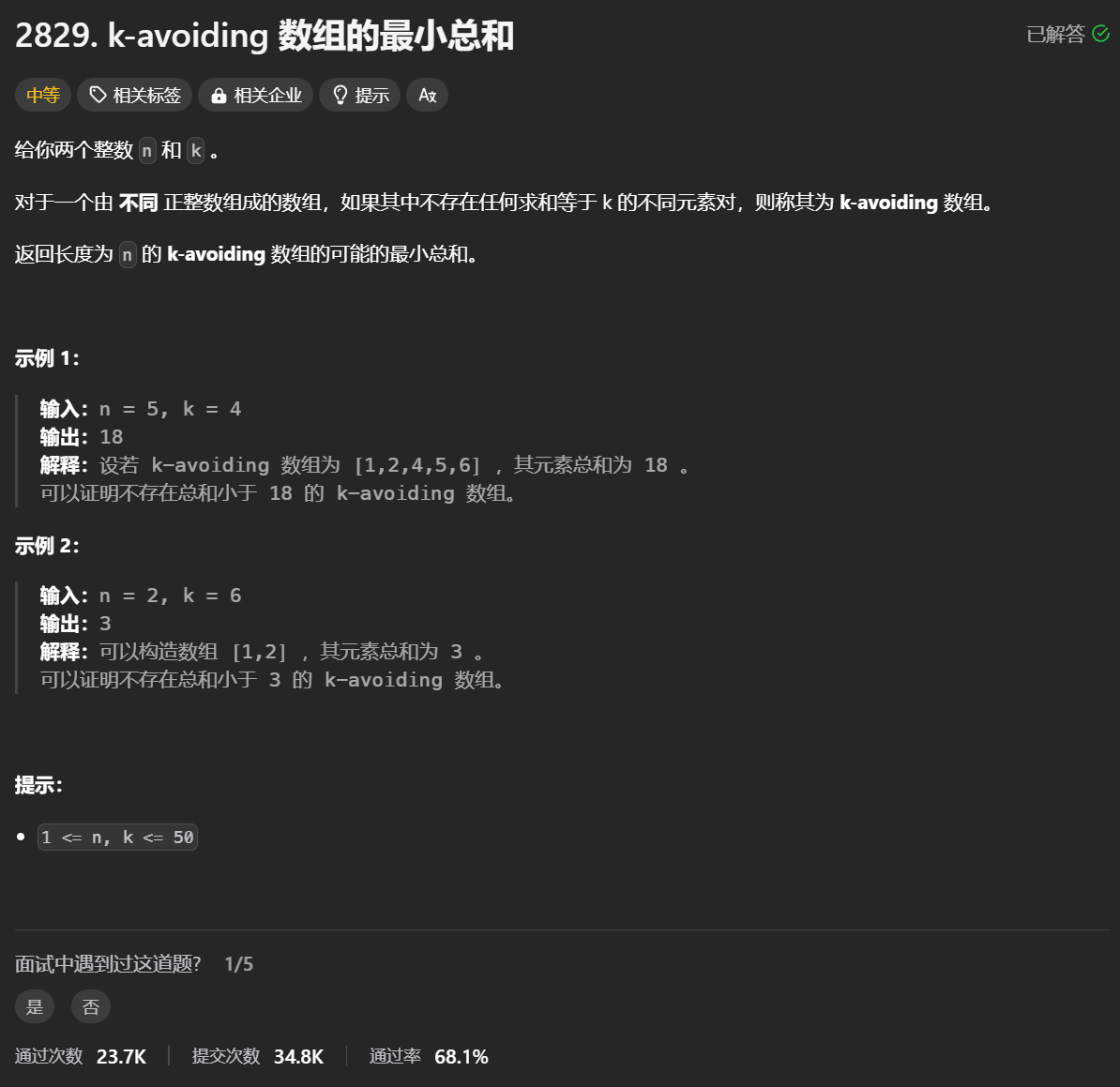
思路：

利用求和公式。

解题步骤：

1.计算 m:
m 表示我们可以安全取用的最大连续整数数量（从1开始），这些数不会违反两数之和等于 k 的条件
k/2 是临界点，因为超过这个值后，数字开始可能与前面的数字配对等于 k
2.公式求和·：
前 m 个数的和：使用等差数列求和公式 m*(m+1)/2
剩余 n-m 个数的和：从 k 开始取数，确保不与前面的数冲突，求和公式为 (k + (k + (n-m-1))) * (n-m)/2 = (2k + n-m-1) * (n-m)/2
合并两部分：(m*(m+1) + (2k + n-m-1)*(n-m)) / 2。
3.返回数组。

代码：

#define MIN(a, b) ((b) < (a) ? (b) : (a))

int minimumSum(int n, int k) {
    int m = MIN(k / 2, n);
    return (m * (m + 1) + (k * 2 + n - m - 1) * (n - m)) / 2;
}

class Solution {
    public int minimumSum(int n, int k) {
        int m = Math.min(k / 2, n);
        return (m * (m + 1) + (k * 2 + n - m - 1) * (n - m)) / 2;
    }
}

复杂度：

O（1）
O（1）