(513B1)codeforce

B1. Permutations

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

You are given a permutation p of numbers 1, 2, ..., n. Let's define f(p) as the following sum:

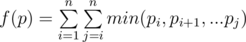
Find the lexicographically m-th permutation of length n in the set of permutations having the maximum possible value of f(p).

Input

The single line of input contains two integers n and m (1 ≤ m ≤ cntn), where cntn is the number of permutations of length n with maximum possible value of f(p).

The problem consists of two subproblems. The subproblems have different constraints on the input. You will get some score for the correct submission of the subproblem. The description of the subproblems follows.

• In subproblem B1 (3 points), the constraint 1 ≤ n ≤ 8 will hold.
• In subproblem B2 (4 points), the constraint 1 ≤ n ≤ 50 will hold.

Output

Output n number forming the required permutation.

Sample test(s)

input

2 2

output

2 1 

input

3 2

output

1 3 2 

Note

In the first example, both permutations of numbers {1, 2} yield maximum possible f(p) which is equal to 4. Among them, (2, 1) comes second in lexicographical order.

这个题主要是让你求 根据公式，然后求f(p)最大值的情况下，第m个排列是什么

这是简单版本，所以暴力搞

#include<iostream>

#include<cstdio>
#include<string.h>
#include<string>
#include<set>
#include<algorithm>
#include<cmath>


#define ll __int64
#define MAX 1000009
using namespace std;


/*
纯纯的暴力···  1<=n<=8 暴力可搞
最开始没有想到公式的意思，数学好渣ing
高数还在大挂
*/
int a[MAX];


int solve(int n)
{
    int sum = 0;
    int _min;
    for(int i = 1; i<=n; i++)
    {
        for(int j = i; j<=n; j++)
        {
            _min = MAX;
            for(int k = i; k<=j; k++)
            {
                _min = min(_min,a[k]);
            }
            sum+=_min;
            //cout<<sum<<endl;
        }
    }
    return sum;
}
int main()
{
    int n,m;
    int i,j;
    int maxn;
    while(~scanf("%d%d",&n,&m))
    {
        maxn = -MAX;
        for(i = 1; i<=n; i++)
            a[i] = i;
        do
        {
            maxn = max(maxn,solve(n));
        }
        while(next_permutation(a+1,a+n+1));
        cout<<maxn<<endl;
        sort(a+1,a+n+1);
        do
        {
            if(maxn == solve(n))
            {
                m--;
                if(m==0)break;
            }
        }
        while(next_permutation(a+1,a+n+1));
        for(i=1; i<=n; i++)
        {
            if(i!=1)
            {
                cout<<" ";
            }
            cout<<a[i];
        }
        cout<<endl;
    }


    return 0;
}