机器学习（三）：逻辑回归之从理论到实践

文中的代码和数据集下载地址：
https://github.com/TimePickerWang/MachineLearningInAction

一、基本理论

　　逻辑回归是一个二值型的分类器，它是利用Sigmoid函数来进行分类的，Sigmoid函数的表达式如下：

$g(z) = \frac{1}{1+e^{-z}}$

其函数图像如下图：

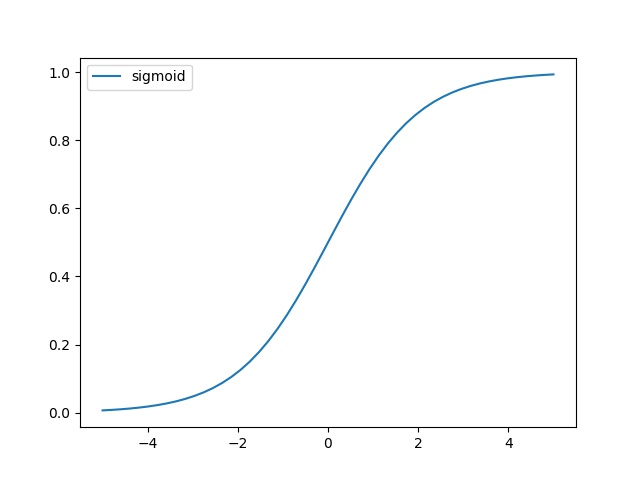
结合表达式可以知道：
$当z=0时，g(z)=0.5$
$当z>0时，g(z)>0.5$，且随着z的增大，g(z)会越来越接近1
$当z<0时，g(z)<0.5$，且随着z的减小，g(z)会越来越接近0

利用这一特性，我们可以进行这样一种分类方式：
当输入$z>0.5$时，把样本分为1类
当输入$z<0.5$时，把样本分为0类

那么$z$具体是什么呢？假设每一个样本有n个特征：{${x_1,x_2,x_3......x_n}$}，则：

$z=w_0x_0+w_1x_1+w_2x_2+...+w_nx_n$
　　
　　其中， $x_0=1$是一个常数，表示一个偏差量。 $w_0,w_1,w_2,...w_n$可以理解为每一个特征的权重，我们的目的就是寻求一组 $w_0,w_1,w_2,...w_n$，使得分类正确的概率尽可能的大。

　　那么问题来了，怎么表示分类正确的概率呢？假设有一个样本$i$，其类标签是$y(y=0或1)$，则可以利用上面提到的“$g(z)$”表示样本$i$为类1的概率，由于Sigmoid的值域为（０,１），所以可以令”$1-g(z)$”表示样本为类0的概率。则样本$i$分类正确的概率可以表示如下：

$p=g(z)^y(1-g(z))^{1-y}$

上式中，当$y=1$时，$p=g(z)$；当$y=0$时，$p=1-g(z)$。所以无论样本