本文深入探讨了自然语言处理中词向量的重要性，对比了one-hot vector与基于SVD的词向量表示方法，并详细介绍了word2Vec算法的两大模型：CBOW和Skip-Gram。此外，文章还讲解了Negative Sampling技术，以解决高维计算效率问题。
word2Vec 概述、算法实现过程
一、word2Vec 是什么，作用什么
背景
自然语言处理中，比如翻译，问答系统，都需要一个基础：如何用数据表示单个的词呢？只有很好的表征单个词以后，才能后续输入到模型中去训练。这样的表征能使每个词不一样，最好能反映出词更多的自身特性。
二、有哪些词向量表示方法
one-hot vector
这种是比较容易想到的表示方法：
每个单词表示成一个 V*1 维的向量，V 为整个词汇表的长度，向量中单词对应的行为1，其他为0；这样词汇表中每个词都不一样。假设词汇表中第一个单词是aardvark,第二个是a,最后一个是zebra，则形式可以表示为：
a
a
r
d
v
a
r
k
⇀
=
[
1
0
.
.
.
0
]
,
a
⃗
=
[
0
1
.
.
.
0
]
,
.
.
.
,
z
e
b
r
a
⇀
=
[
0
0
.
.
.
1
]
\overrightharpoon{aardvark} = \left[ \begin{matrix} 1 \\ 0 \\ . \\ . \\ . \\ 0 \\ \end{matrix} \right], \vec a = \left[ \begin{matrix} 0 \\ 1 \\ . \\ . \\ . \\ 0 \\ \end{matrix} \right], ... , \overrightharpoon{zebra} = \left[ \begin{matrix} 0 \\ 0 \\ . \\ . \\ . \\ 1 \\ \end{matrix} \right]
aardvark=⎣⎢⎢⎢⎢⎢⎢⎡10...0⎦⎥⎥⎥⎥⎥⎥⎤,a=⎣⎢⎢⎢⎢⎢⎢⎡01...0⎦⎥⎥⎥⎥⎥⎥⎤,...,zebra=⎣⎢⎢⎢⎢⎢⎢⎡00...1⎦⎥⎥⎥⎥⎥⎥⎤
缺点：
- 英语中大概有1300万个符号，这样词汇表维度V 将非常大。
- 词语直接是有关联的，比如
hotel to motel,man to woman,但是这样表示后，
h o t e l ⇀ T ∗ m o t e l ⇀ = 0 \overrightharpoon{hotel}^{T} * \overrightharpoon{motel} = 0 hotelT∗motel=0
任意两向量内积都为0，每个词之间没有任何的关系。
所以one-hot这并不是个很好的表征方法
基于SVD的方法
1、Word-Document Matrix
针对one-hot编码不能表达词与词之间关系的问题，我们可以统计文档中单词的数量，以此来表征词之间关系。比如 “banks”, “bonds”, “stocks”, "money"这些词出现在同一篇文档中概率很大。
用
X
i
,
j
\Chi_{i,j}
Xi,j 来表示词-文档矩阵。i 表示词的索引,维度V;j 表示文档的索引，维度记为M。通过训练大量文档，最终可以得出词矩阵，
X
i
,
j
\Chi_{i,j}
Xi,j的维度
R
V
∗
M
\Reals^{V*M}
RV∗M。可以发现，此矩阵维度仍然没有得到改进。
2、Window based Co-occurrence Matrix（基于窗口的共现矩阵）
假设语料库只有三句：
- I enjoy flying.
- I like NLP.
- I like deep learning.
共现矩阵试图表示出词语之间共同出现的次数，假设窗口为1，即只考虑相邻的单词，那么共现矩阵可以表示为：
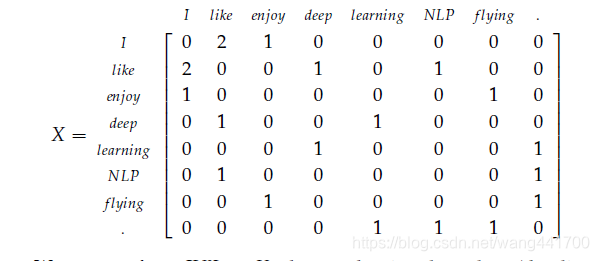
如果词汇表长度为V, 那么矩阵维度为 R V ∗ V \Reals^{V*V} RV∗V。
针对以上两种方法，可以看出矩阵是稀疏的，维度也过大。可以通过奇异值分解SVD来将得到的矩阵降维。大体思路是仍能保证大部分特征不丢失的前提下，找到一些维度更低的矩阵，比如 R V ∗ 100 \Reals^{V*100} RV∗100，来替代以前 R V ∗ 100 \Reals^{V*100} RV∗100的矩阵，这样来降为。具体方法可以参考PAC。
3、缺点
针对上述两种方法即使我们可以降维，可以表示词之间的关联性，但是还存在许多其他问题：
- 矩阵维度会经常变动，比如Word-Document Matrix中增加了新的训练文档进来。
- 矩阵太稀疏，因为共现的词数量相对太少
- SVD 降为因为维度过高会很耗时
- 有一些常用单词不平衡问题，比如"the", “he”, "has"的共现率就很高
基于迭代的方法
不同于上面的基于大量数据集，一次性统计单词的词频。我们希望有种方法来找到一个词模型可以表征出当给定上下文单词后，能给出哪个单词出现概率最大，而且最好可以通过一次次的迭代来改进模型。比如"The cat jumped over the puddle."，当‘jumped’,缺失时，是否可以根据上下文单词"The * jumped over the puddle."推断出’jumped’呢？
如何用数学来表述这种概率呢？
∏
P
(
w
1
,
w
2
,
.
.
.
,
w
n
)
=
∏
i
=
2
n
P
(
w
i
∣
w
i
−
1
)
\prod P(w_1,w_2,...,w_n) = \prod_{i=2}^{n} P(w_i|w_{i-1})
∏P(w1,w2,...,wn)=i=2∏nP(wi∣wi−1)
上式表明了句子(每个词出现在指定序列位置)出现的概率大小。
对于上面的例句，当cat出现时，后面一个词为jumped 的概率是不是比其他词要更大呢。当然这个公式模型只考虑了相邻的单词，没有考虑到整个句子，但是这个基本思想是很重要的，基于这个思想，我们引入了后续几个模型。
1、Continuous Bag of Words Model (CBOW)
思想
对于"The cat _ over the puddle."，我们想通过上下文词预测出缺失的是个什么词。即通过上下文词来预测中心词。
思路
首先需要一个损失函数来衡量单词训练样本结果的好坏，然后使用梯度下降算法来优化参数。
这里输入数据为词的one-hot表示，维度记为
R
V
∗
1
\Reals^{V*1}
RV∗1；输出数据也为词的one-hot表示，维度记为
R
V
∗
1
\Reals^{V*1}
RV∗1。对结果使用交叉熵cross-entropy损失函数以此来进行反向传播进行梯度优化。
H
(
y
,
y
^
)
=
−
∑
i
=
1
V
y
i
∗
l
o
g
(
y
i
^
)
H(\mathbf{y},\hat{\mathbf{y}}) = -\sum_{i=1}^{V} y_{i} * log(\hat{y_{i}})
H(y,y^)=−i=1∑Vyi∗log(yi^)
因为输出结果y也是on-hot形式，只有对应单词索引位置为1，其他全为0，所以上面损失函数可简化为
H
(
y
,
y
^
)
=
−
y
i
∗
l
o
g
(
y
i
^
)
H(\mathbf{y},\hat{\mathbf{y}}) = -y_{i} * log(\hat{y_{i}})
H(y,y^)=−yi∗log(yi^)
i为待预测单词的索引，即’jumped’ one-hot中为1的位置。
有了损失函数，通过反向传播，梯度下降就可以得到我们想要的模型。
具体步骤
以前知道大概步骤，但是具体怎么训练出来的词向量模型一直没有搞清楚，怎么从look up table（word embedding）算出最后的维度为 R V ∗ 1 \Reals^{V*1} RV∗1的结果。我也是通过学习资料，然后配合代码看才把具体训练过程搞明白。对于算法细节本身，通过代码来了解不失为一种好方法。
上图W即为对应的词向量，训练过程中还有个额外的
W
′
W'
W′ 需要训练。
- 选定一个中心词 x c x^c xc， 上下文窗口宽度m, 则输入数据为 ( x c − m , . . . , x c − 1 , x c + 1 , . . . , x c + m ) (x^{c-m}, . . . , x^{c-1}, x^{c+1}, . . . , x^{c+m}) (xc−m,...,xc−1,xc+1,...,xc+m)。 每个x 为one-hot编码维度为 R V ∗ 1 \Reals^{V*1} RV∗1.
- 词向量 W ， 维 度 为 V ∗ N W，维度为V*N W，维度为V∗N(N为自己设定的数), 计算出上下文的词向量： ( v c − m = W x c − m , v c − m + 1 = W x c − m + 1 , . . . , v c + m = W x c + m ) (v^{c-m} = Wx^{c-m}, v^{c-m+1} = Wx^{c-m+1}, . . ., v^{c+m} = Wx^{c+m}) (vc−m=Wxc−m,vc−m+1=Wxc−m+1,...,vc+m=Wxc+m)。可看出上下文词向量即为W中对应单词所在的一行。输入层的每个单词与矩阵W相乘得到的向量的就是我们想要的词向量（word embedding），这个矩阵（所有单词的word embedding）也叫做look up table。也就是说，任何一个单词的onehot乘以这个矩阵都将得到自己的词向量。 V 的 维 度 为 ( N , ) V的维度为(N,) V的维度为(N,)
- 将所有上下文词求均值：
v ^ = v c − m + v c − m + 1 + . . . + v c + m 2 m \hat{v} = \cfrac{v^{c-m} + v^{c-m+1} + ... + v^{c+m}} {2m} v^=2mvc−m+vc−m+1+...+vc+m - z = W ′ v ^ z = W'\hat{v} z=W′v^
- y ^ = s o f t m a x ( z ) \hat{y} = softmax(z) y^=softmax(z)
- 根据损失函数： H ( y , y ^ ) = − y i ∗ l o g ( y i ^ ) H(\mathbf{y},\hat{\mathbf{y}}) = -y_{i} * log(\hat{y_{i}}) H(y,y^)=−yi∗log(yi^)，和反向传播梯度下降进行求解最优的 W W W,即为词向量。
其中梯度下降过程需要用链式求导，算出softmax，sigmoid等函数的微分，这里不再细述。
2、Skip-Gram Model
和CBOW类似，不同的是输入变为了一个，即步骤3有差异，不用再求平均；预测输出变为了多个(上下文词)。
梯度下降时，针对每个输出，都需要更新词向量参数。
3、Negative Sampling
对于上面两种算法，没次计算都会涉及到维度为
V
V
V（词汇表长度）的softmax运算，比较慢。负采样思想是采集句子中相关联的词(o,c)，句子外无关的词对(k，c), 使其损失函数最小。
负样本数为K，正确答案为o，那么有o∉{1,…,K}。负采样损失函数定义如下：
J
n
e
g
−
s
a
m
p
l
e
(
o
,
v
c
,
U
)
=
−
l
o
g
(
σ
(
u
o
T
v
c
)
)
−
∑
k
=
1
K
l
o
g
(
σ
(
−
u
k
T
v
c
)
)
J_{neg-sample}(\boldsymbol{o}, \boldsymbol{v}_{c}, \boldsymbol{U}) = − log(\sigma(\boldsymbol{u}_{o}^{T} \boldsymbol{v}_{c})) - \sum\limits_{k=1}^{K} log(\sigma(-\boldsymbol{u}_{k}^{T} \boldsymbol{v}_{c}))
Jneg−sample(o,vc,U)=−log(σ(uoTvc))−k=1∑Klog(σ(−ukTvc))
其中
σ
(
x
)
=
1
1
+
e
−
x
\sigma(x) = \frac{1}{1 + e^{-x}}
σ(x)=1+e−x1
为logistic 函数。
利用反向传播,不断更新
d
u
o
，
d
u
k
。
u
即
为
词
向
量
du_{o}，du_{k}。 \boldsymbol{u} 即为词向量
duo，duk。u即为词向量。
三、程序实现word2Vec
借用斯坦福大学 cs224n 的作业1 的代码来说明具体实现细节参考
1、CBOW
def cbow(currentWord, C, contextWords, tokens, inputVectors, outputVectors,
dataset, word2vecCostAndGradient=softmaxCostAndGradient):
cost = 0.0
gradIn = np.zeros(inputVectors.shape)
gradOut = np.zeros(outputVectors.shape)
### YOUR CODE HERE
predicted_indices = [tokens[word] for word in contextWords]
predicted_vectors = inputVectors[predicted_indices]
predicted = np.sum(predicted_vectors, axis=0) # why not divid the 2*C ?, got it. softmax(x)=softmax(x/(2*C))
target = tokens[currentWord]
cost, gradIn_predicted, gradOut = word2vecCostAndGradient(predicted, target, outputVectors, dataset)
for i in predicted_indices:
gradIn[i] += gradIn_predicted
### END YOUR CODE
return cost, gradIn, gradOut
对应 具体步骤 章节来说明。其中入参，outputVectors 即为cbow 图中的
W
′
W'
W′， inputVectors 为对应的词向量
W
W
W
softmaxCostAndGradient(predicted, target, outputVectors, dataset) 的predicted 对应 具体步骤 章节中的
y
^
\hat{y}
y^，target对应
y
y
y, softmaxCostAndGradient函数将返回的
c
o
s
t
,
d
W
′
,
d
v
^
cost, dW', d\hat{v}
cost,dW′,dv^。
即gradOut为
d
W
′
dW'
dW′, gradIn_predicted 为
d
v
^
d\hat{v}
dv^, 要求
d
W
dW
dW 的词向量
W
W
W的梯度，由步骤2所示，
(
v
c
−
m
=
W
x
c
−
m
,
v
c
−
m
+
1
=
W
x
c
−
m
+
1
,
.
.
.
,
v
c
+
m
=
W
x
c
+
m
)
(v^{c-m} = Wx^{c-m}, v^{c-m+1} = Wx^{c-m+1}, . . ., v^{c+m} = Wx^{c+m})
(vc−m=Wxc−m,vc−m+1=Wxc−m+1,...,vc+m=Wxc+m)，所以
d
W
dW
dW 的梯度更新仅仅影响对应上下文词所在索引的
W
W
W， 于是会有代码：
for i in predicted_indices:
gradIn[i] += gradIn_predicted
备足，要看懂代码，需要知道反向传播中softmax等函数的中微分，可以参考这里；反向传播中的矩阵维度也挺让人头大，可以配合代码debug看。
2、Skip-Gram
代码类似，只不过梯度更新时不一样，因为有多个 中心词->上下文词 的映射,所以会多次更新 d W dW dW， d W ′ dW' dW′的梯度
def skipgram(currentWord, C, contextWords, tokens, inputVectors, outputVectors,
dataset, word2vecCostAndGradient=softmaxCostAndGradient):
cost = 0.0
gradIn = np.zeros(inputVectors.shape)
gradOut = np.zeros(outputVectors.shape)
### YOUR CODE HERE
cword_idx = tokens[currentWord]
vhat = inputVectors[cword_idx]
for j in contextWords:
u_idx = tokens[j]
c_cost, c_grad_in, c_grad_out = \
word2vecCostAndGradient(vhat, u_idx, outputVectors, dataset)
cost += c_cost
gradIn[cword_idx] += c_grad_in
gradOut += c_grad_out
### END YOUR CODE
return cost, gradIn, gradOut
3、Negative Sampling
negSamplingCostAndGradient 函数返回(cost、正样本梯度、负样本梯度)
扫一扫
3191
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
