python Erdos-Renyi图的由来场景用途示例

python Erdos-Renyi图的由来用法场景用途示例–点击此处看全文

1. 由来

Erdos-Renyi图是一种随机图模型，由数学家Paul Erdos和Alfred Renyi于1959年提出。它以两个参数为基础：节点数量n和边的概率p。

在Erdos-Renyi图中，所有可能的节点对之间都有一个连接，并且每个连接以概率p独立地存在。这意味着对于每对节点，以概率p选择将它们连接起来。

在Python的networkx库中，可以使用nx.erdos_renyi_graph(n, p)函数创建Erdos-Renyi图。其中，n是节点数量，p是边的概率。

示例：

import networkx as nx

# 创建一个具有100个节点和边概率为0.01的Erdos-Renyi图
G = nx.erdos_renyi_graph(15, 0.2)
pos = nx.spring_layout(G)
nx.draw(G, pos, with_labels=True)
plt.show()

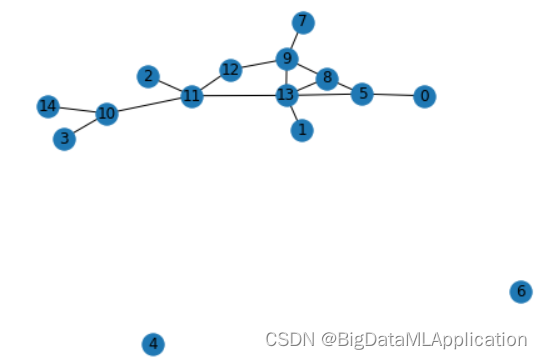
2. 参数用法

erdos_renyi_graph

erdos_renyi_graph(n, p, seed=None, directed=False)

返回一个随机图，也称为Erdős-Rényi图或二项式图。

模型根据概率p选择每条可能的边。

参数：

• n：节点数。
• p：边创建的概率。
• seed：整数、随机状态或None（默认值），用于指示随机数生成的状态。参见Randomness。
• directed：布尔值，可选（默认为False）。如果为True，则返回有向图。

另请参阅：

• fast_gnp_random_graph

注意事项：

• 该算法的时间复杂度为O(n^2)。对于稀疏图（即小的n值），fast_gnp_random_graph()是更快的算法。
• binomial_graph()和erdos_renyi_graph()是gnp_random_graph()的别名。

3. 适用场景

Erdos-Renyi图在以下情况下适用：

2.1 研究随机图的性质和行为

2.2 评估社区检测算法的性能

2.3 模拟各种类型的网络

2.4 设计和测试图算法和网络分析方法

4. 示例

4.1 研究随机图的性质和行为

import networkx as nx
import matplotlib.pyplot as plt

# 创建一个具有100个节点和边概率为0.1的Erdos-Renyi图
G = nx.erdos_renyi_graph(100, 0.1)

# 绘制图形
pos = nx.spring_layout(G)
nx.draw(G, pos, with_labels=True)
plt.show()

# 计算图的平均度数
average_degree = sum(dict(G.degree()).values()) / len(G)
print