【oj题】环形链表

最新推荐文章于 2025-07-28 14:53:07 发布

原创最新推荐文章于 2025-07-28 14:53:07 发布 · 396 阅读

15 ·

CC 4.0 BY-SA版权

文章标签：

#链表 #数据结构

数据结构专栏收录该内容

1 篇文章

订阅专栏

一. OJ链接：环形链表

【思路】快慢指针

编辑【扩展问题】为什么快指针每次走两步，慢指针走一步可以解决问题？

编辑【扩展问题】快指针一次走3步，走4步，...n步行吗？

二. OJ链接：环形链表||

一. OJ链接：环形链表

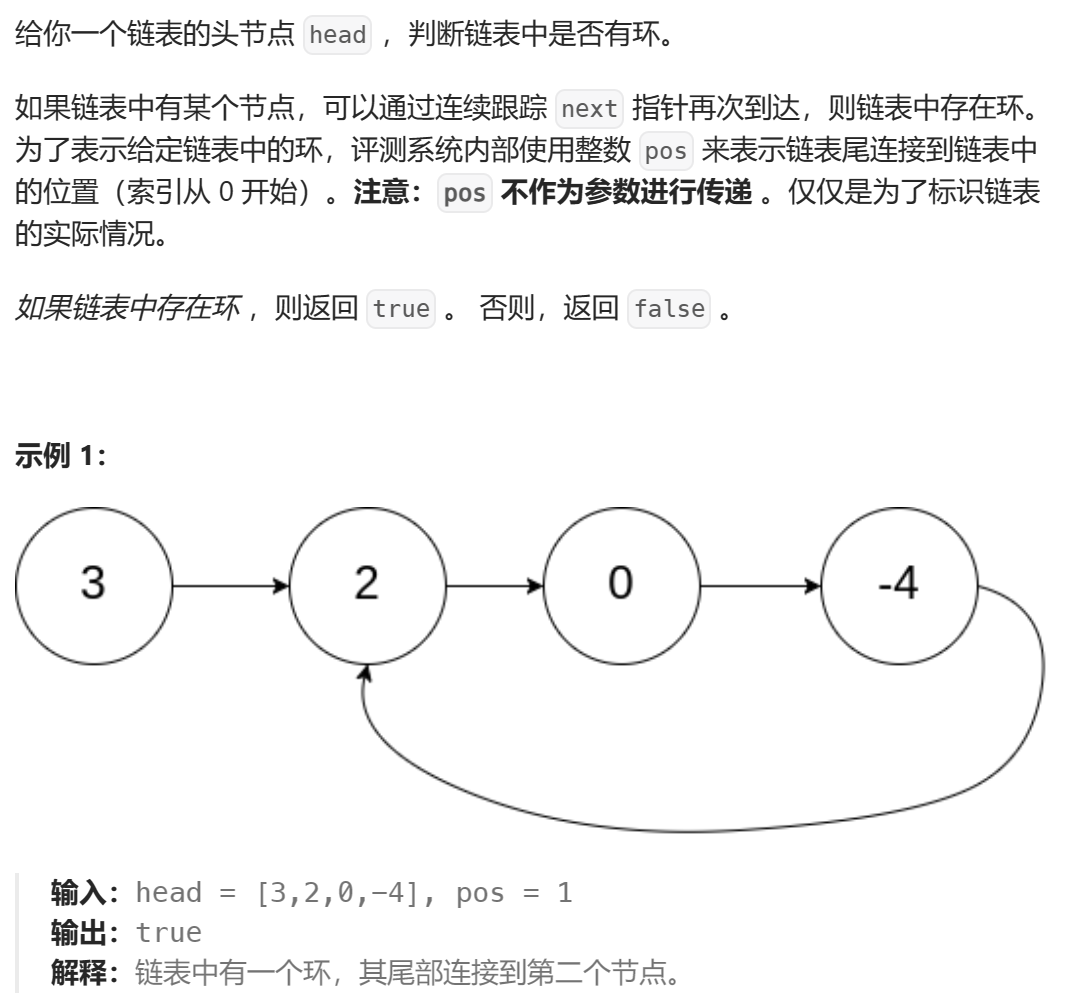
【思路】快慢指针

即慢指针一次走一步，快指针一次走两步，两个指针从链表起始位置开始运行，如果链表带环则一定会在环中相遇，否则快指针率先走到链表的末尾。
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */
typedef struct ListNode ListNode;
bool hasCycle(struct ListNode *head) 
{
    ListNode* fast , *slow;
    fast = slow = head;
    while(fast && fast->next)
    {
        fast = fast->next->next;
        slow = slow->next;
        if(fast == slow)
        return true;
    }   
    return false;
}

【扩展问题】为什么快指针每次走两步，慢指针走一步可以解决问题？

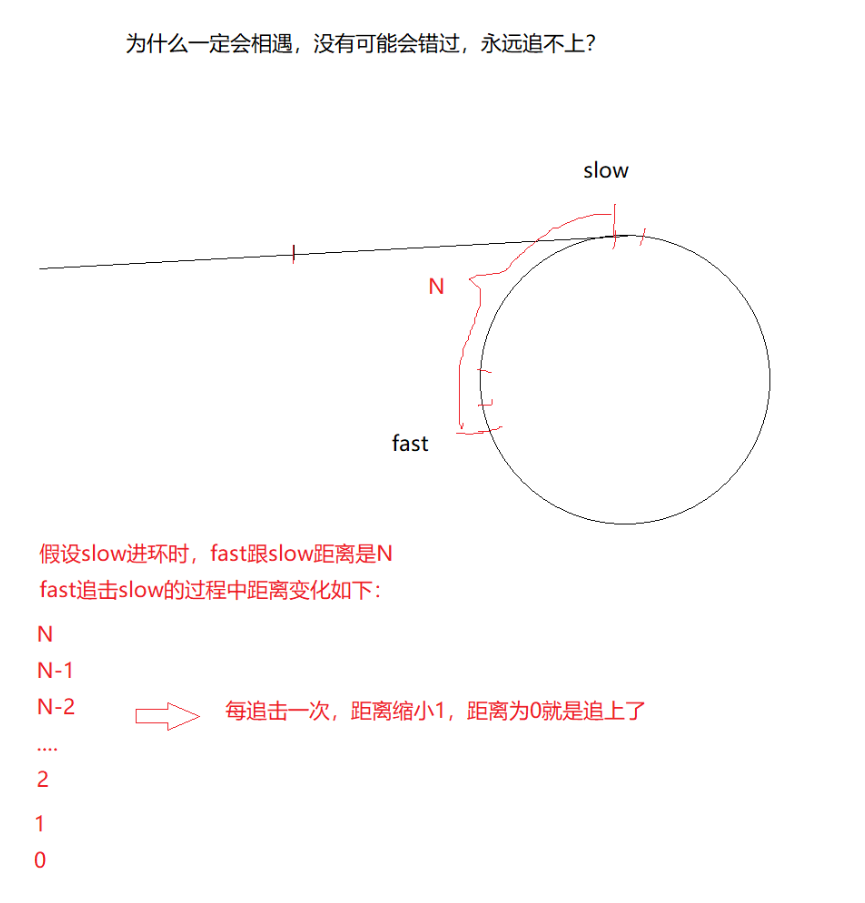
        如果链表不带环，两个指针一定不会相遇，因为fast = 2slow

        假设链表带环，两个指针最后都会进入环，快指针先进环，慢指针后进环。

        当慢指针刚进环时，可能就和快指针相遇了，最差情况下两个指针之间的距离刚好就是环的长度-1。

        此时，两个指针每移动一次，之间的距离就缩小一步。因此，在慢指针走到一圈之前，快指针肯定是可以追上慢指针的，即相遇。

【扩展问题】快指针一次走3步，走4步，...n步行吗？

假设快指针一次走3步，慢指针一次走1步

同理可证，快指针走4,5……也行

二. OJ链接：环形链表||

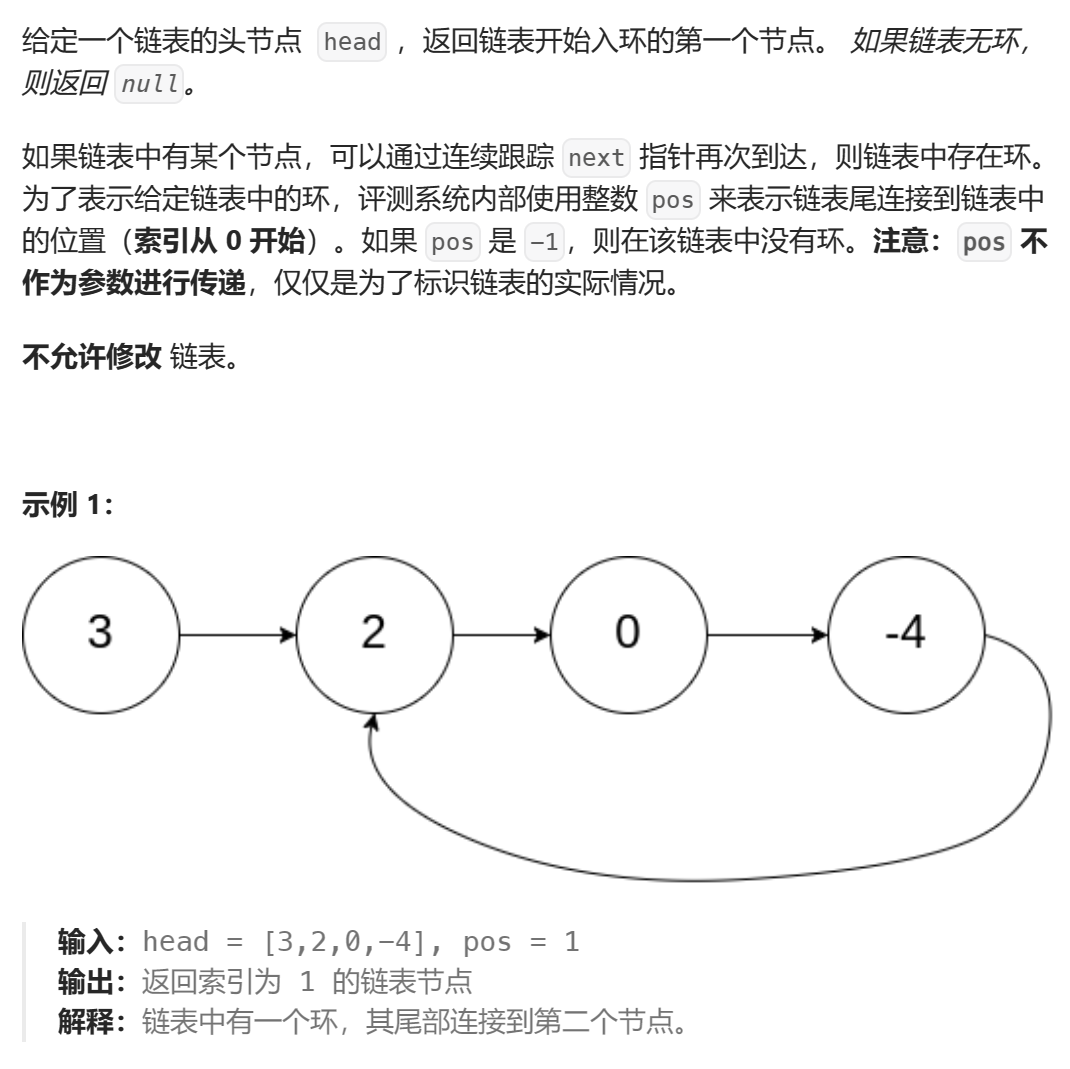
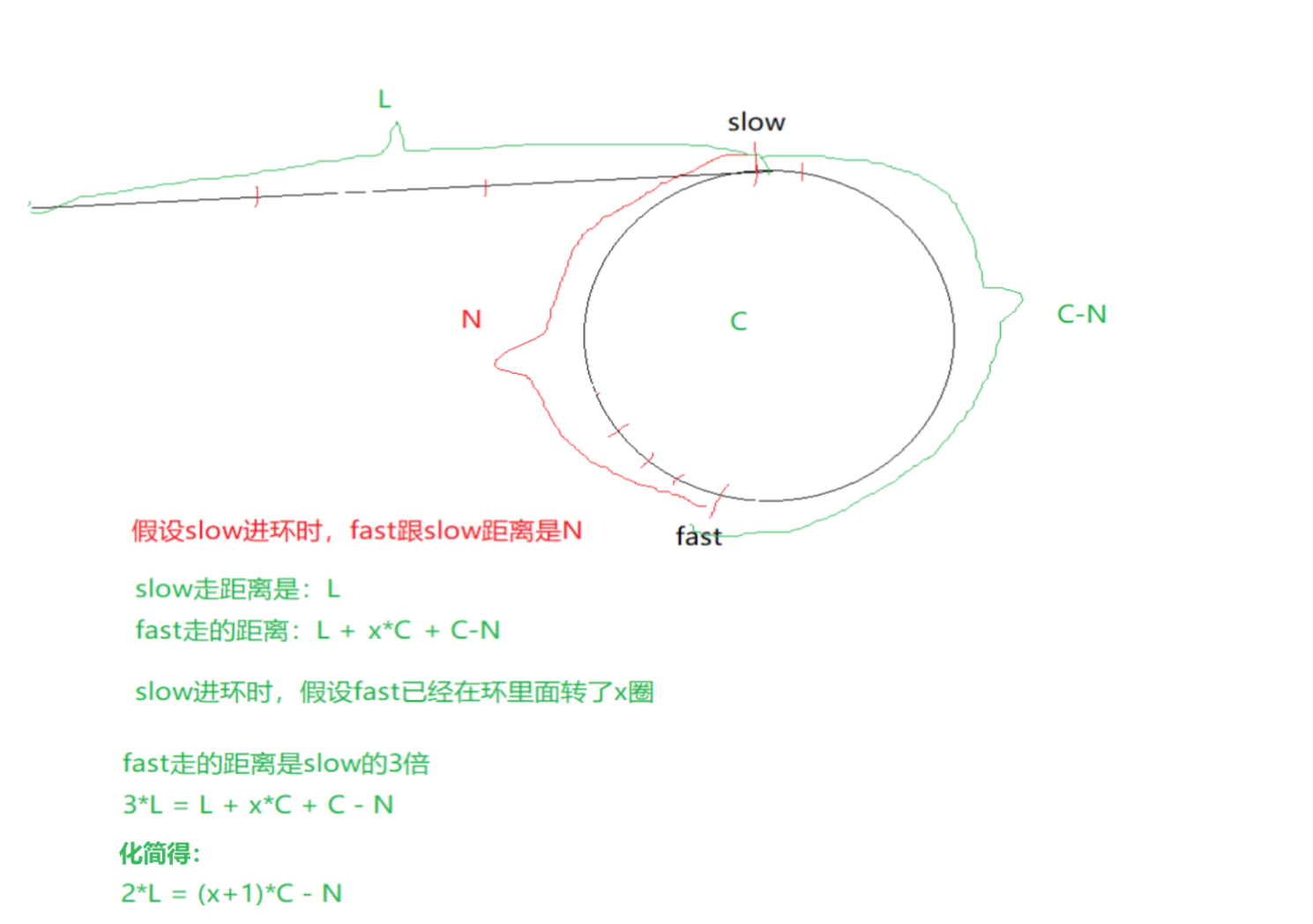
相遇时，slow指针与fast指针走的路程

head指针走L步，meet指针走C-N步，head指针和meet指针相遇，此时就是环的第一个节点

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */
struct ListNode* detectCycle(struct ListNode* head) {
    struct ListNode *slow = head, *fast = head;
    while (fast != NULL && fast->next) 
    {
        slow = slow->next;
        fast = fast->next->next;
        if (fast == slow) {
            struct ListNode *ptr = head, *meet = slow;
            while (ptr != meet) {
                ptr = ptr->next;
                meet = meet->next;
            }
            return ptr;
        }
    }
    return NULL;
}