论文《Feature Generation by Convolutional Neural Network for Click-Through Rate Prediction》

最新推荐文章于 2023-07-17 16:42:10 发布

原创最新推荐文章于 2023-07-17 16:42:10 发布 · 2.2k 阅读

5 ·

CC 4.0 BY-SA版权

pytorch 专栏收录该内容

28 篇文章

订阅专栏

本文介绍了华为方舟实验室等团队在CTR预测上的创新模型。该模型创新了特征交互方法，将新老特征拼接输入分类器可提升效果。分析了MLP和CNN在CTR问题中的不足，给出计算部分的详细过程，最后提到了pytorch代码实现及遇到的性能问题。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

前言

Bin Liu1, Ruiming Tang‡ 1, Yingzhi Chen⋆ 2, Jinkai Yu1, Huifeng Guo1, Yuzhou Zhang1
1华为方舟实验室和2JNU的实习生做的。
论文地址：https://arxiv.org/pdf/1904.04447
实现语言：pytorch

模型概述

如果我们把现有的关于CTR预测的各种state-of-the-art模型作为积木来看，可以统称为classifier model。
在这块积木之前的积木，可以称为feature extraction model或者feature interaction model。

本文的创新之处就在于，创新了一种feature interaction方法，可以对feature进行augment，然后将new_features和old_features拼接在一起，输入到其他任何classifier中，都能提高它们的效果。

听上去挺神奇的，有点像早些年的xx鸡精广告，无论是烹饪烘焙熬汤炒菜，加上一点味道都会提升。

作者的思路是这样的。
1.为什么Multi-layer Perceptron在CTR问题中表现不好？

写作MLP（多层感知机），就是传统的DNN网络。
首先，我们知道CTR问题中特征很稀疏。
于是，我们知道DNN网络的参数是海量的。
进一步地，想从海量的参数中寻找到最优化解，求解难度就无穷高。
原文(due to that useful feature interactions are usually sparse,
it is rather difficult for MLP to learn such interactions from a huge
parameter space)
这里的逻辑，怎么寻思怎么不对劲。
作者举了个例子，比如有age,gender,height三个特征，假设只跟age和gender有关，那么我们希望height的参数趋向于0，但在反向传播中这是很难做到的。
这句话我又觉得有点疑问了，整的好像其他DNN模型中没有参数趋0问题似的？

2.为什么CNN在CTR问题中表现不太好

这个很好理解。CNN只关注neighbour pattern，而忽略global pattern。
所以无脑使用CNN并不可取。
虽然CNN有着降低参数量，减少optimizing difficulty的良好特性。

于是机智的中国人就想到把两种方法结合一下。
如果我用CNN出来的neighbour pattern，接上几层MLP，不就又有局部又有全局了吗！

小天才嘛！
原文管这叫 completement each other

整个图大概长这样。
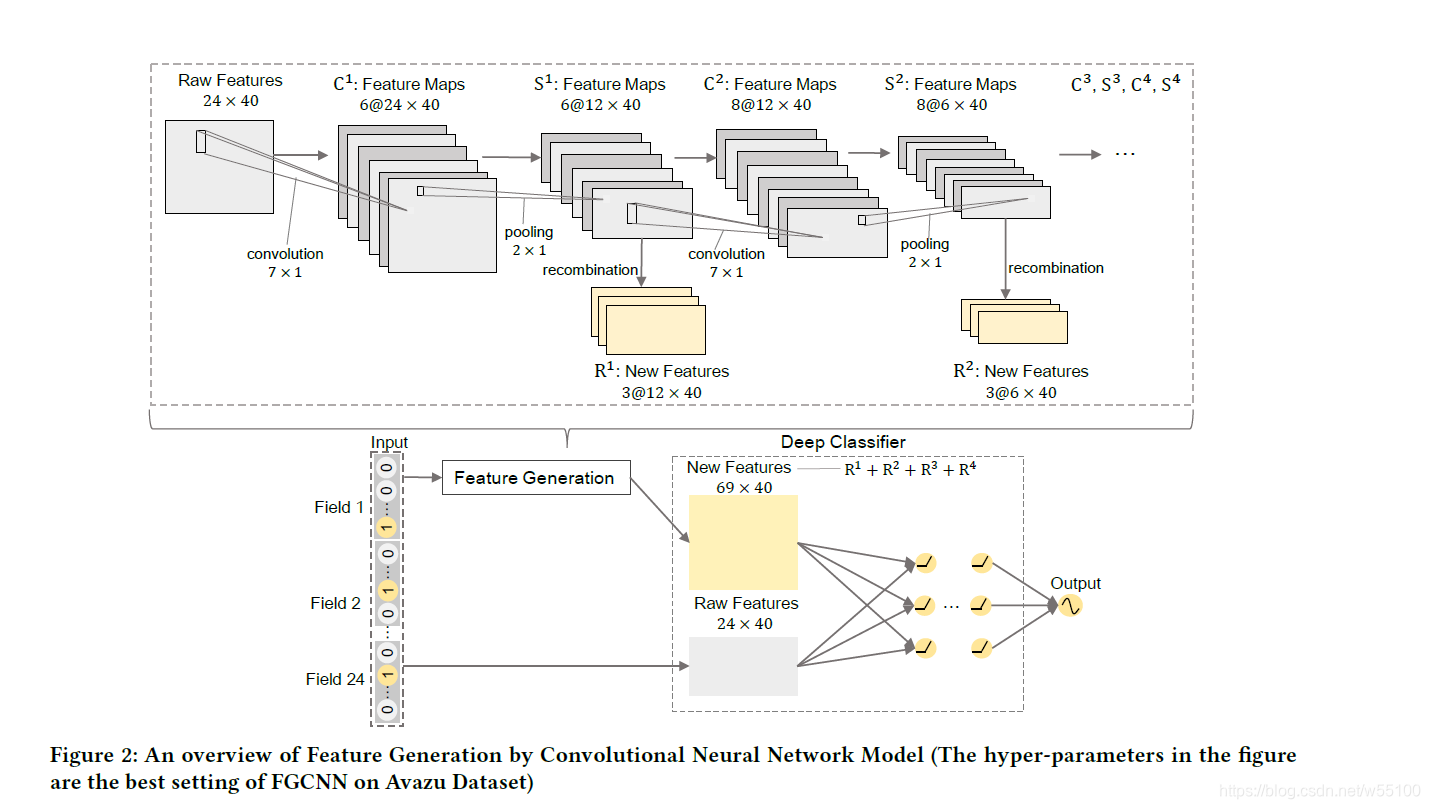
在这里插入图片描述
看图是绝对看不懂的。
没关系，我们往下走。

计算部分

假设我们有 $n_f$ 个field，全部经过embedding变成了形状为 $n_f, k)$ 的矩阵 $E$ ，然后 $c l o n e$ 一份 $E$ ，得到 $E^{'}$ 。

我们有 $4* \{ Conv,Max-pooling, Recombination \}$
每个 $Conv^i$ 有 $n_c^i$ 个filter
4层网络的 $f i l t e r s = (6, 8, 10, 12)$ 。
方便起见，我们假设filter的size统一为 $(7, 1)$ 。
max-pooling的size统一为 $(2, 1)$
我们希望4层分别输出的新特征向量的乘数为
$n e w = (2, 2, 2, 2)$

第一层

$=(n_f,k), reshape \to (n_f,k,1)$
经过6个(7,1)的filter卷积，加上padding，
输出 $tempC^1 = (n_f,k,6)$
经过tanh() 得到 $C^1 = (n_f,k,6)$
经过(2,1)的max-pooling
输出 $P^1=(n_f/2,k,6)$

重点
此处 $P^1$ 有2个去处。
$\text{ } Conv \text{ } Layer$
$P^1$ 作为 $C^2$ 的输入
得到 $C^2=(n_f/2,k,8)$
$P^2=(n_f/4,k,8)$

$2) R e c o m b i n a t i o n$
$P^1$ reorganized $→(nf2,6,k)→(nf2∗6,k)\to ( \frac{n_f}{2},6,k) \to ( \frac{n_f}{2}*6,k)$
进入一个全连接c层
$(nf2∗6,nf2∗new1)=(nf2∗6,nf2∗2)(\frac{n_f}{2}*6, \frac{n_f}{2}*new_1 )=(\frac{n_f}{2}*6, \frac{n_f}{2}*2 )$
得到
$R1=(nf2∗2,k)R^1 = ( \frac{n_f}{2}*2 ,k)$

输出

经过4层，我们得到
$R1=(nf2∗2,k)R^1 = ( \frac{n_f}{2}*2 ,k)$
$R2=(nf4∗2,k)R^2 = ( \frac{n_f}{4}*2 ,k)$
$R3=(nf8∗2,k)R^3 = ( \frac{n_f}{8}*2 ,k)$
$R4=(nf16∗2,k)R^4 = ( \frac{n_f}{16}*2 ,k)$

上式中的2，是我们设好的乘数 $new_i$ 。

在dim=0上concatenate一下，就能得到新特征构成的矩阵 $R = (N, k)$
再与旧特征 $E'=(n_f,k)$ concatenate一下
得到 $new E =(n_f+N,k)$

完成。

然后把这个new E丢进随便哪个classifier里跑一跑，就能发现它很有效。

整体思路和理论都不复杂。
但这是在华为应用商店检验的算法，所以值得尊重一手。

代码部分

FGCNN in pytorch

class ConvPoolRecombine(nn.Module):
    """
    input=(N,C_in,H,W)
    output=(N,newi,H/2,W)
    
    arguments:
        $in_channel = C_in = filters_{i-1}$
        $out_channel = C_out = filters_{i}$
        $new_channel = new_{i}$
        $out_wh = H/2*W$
    """
    def __init__(self,in_channel,out_channel,new_channel,out_wh, device):
        super().__init__()
        
        self.device=device
        self.out_channel = out_channel
        self.new_channel = new_channel
        
        self.conv = nn.Conv2d(in_channel,out_channel,kernel_size=(7,1),stride=1,padding=(3,0)).to(self.device)
        self.tanh = torch.nn.Tanh()
        self.pool = nn.MaxPool2d(kernel_size=(2,1)).to(self.device)
        self.recomb = nn.Linear(out_wh*out_channel,out_wh*new_channel).to(self.device)

    def forward(self,x):
        #x = (N,C_in,H,W)
        batch_size=x.shape[0]
        width = x.shape[3]

        #c = (N,C_out,H,W)
        c = self.conv(x)
        c = self.tanh(c)
        
        #p = (N,C_out,H/2,W)
        p = self.pool(c)
        
        #f = (N,H/2,W,C_out)
        f = p.permute([0,2,3,1]).contiguous()
        #f = (N,H/2*W*C_out)
        f= f.view(batch_size,-1)
        
        #r=(N,H/2,W,C_new)
        r = self.recomb(f).view(batch_size,-1,width,self.new_channel)
        
        #out_r = (N,C_new*H/2,W)
        out_r = r.permute([0,3,1,2]).contiguous().view(batch_size,-1,width)
        
        return p,out_r
        
        
class FGCNN(nn.Module):
    def __init__(self, feature_sizes, use_cuda=True):
        super(FGCNN,self).__init__()
        
        self.feature_sizes = feature_sizes
        self.n_fields = len(feature_sizes)
        self.embd_size = 40
        
        self.channels = [6,8,10,12]

        print('n_fields',self.n_fields)
        print(feature_sizes)
        
        if use_cuda and torch.cuda.is_available():
            print('cuda enabled')
            self.device = 'cuda'
        else:
            self.device = 'cpu'


        self.embd_layers = nn.ModuleList(
            [nn.Embedding(self.feature_sizes[i], self.embd_size) for i in range( self.n_fields)]
        ).to(self.device).double()
        
        
        self.conv1 = ConvPoolRecombine(1,6,2,self.n_field*self.embd_size/2 , self.device)
        self.conv2 = ConvPoolRecombine(6,8,2,self.n_field*self.embd_size/4 , self.device)
        self.conv3 = ConvPoolRecombine(8,10,2,self.n_field*self.embd_size/8, self.device)
        
        N = (self.n_fields/2+self.n_fields/4+self.n_fields/8)*2 # set new_i all equals 2
        self.inpt1_size = self.n_fields*self.embd_size + (N+self.n_fields)*(N+self.n_fields-1)/2
        
        #classifier部分
        self.mlp = nn.Sequential(
                        nn.Linear(self.inpt1_size,2048),
                        nn.BatchNorm1d(2048),
                        nn.ReLU(inplace=True),
                        
                        nn.Linear(inpt1_size,1024),
                        nn.BatchNorm1d(1024),
                        nn.ReLU(inplace=True),
                        
                        nn.Linear(inpt1_size,512),
                        nn.BatchNorm1d(512),
                        nn.ReLU(inplace=True),
                        
                        nn.Linear(inpt1_size,256),
                        nn.BatchNorm1d(256),
                        nn.ReLU(inplace=True),
                        
                        nn.Linear(inpt1_size,1),
                        nn.Sigmoid(),
                    )
    
        self.loss_fn = nn.BCEloss()
       
    def forward(self,idx,value,true_y):
    
        batch_size = idx.shape[0]
        
        results = []    #n_f*(m,k)
        for i , module in enumerate(self.embd_layers):
            #当前为 i_th_field
            batch_idx = train_idx[:,i]         #shape=(m)
            batch_vis = module(batch_idx)      #vi,shape=(m,k),dtype=float32
            batch_xis = train_values[:,i]      #xi,shape=(m),dtype=float64
         
            #我们让每个样本的vi与对应的xi相乘
            #print('type of batch_vis',type(batch_vis),batch_vis.dtype)
            #print('type of batch_xis',type(batch_xis),batch_xis.dtype)
            res = (batch_vis.t())*batch_xis      #(k,m)*(m)=(k,m)
            res = res.t()                           #shape=(m,k)
            results.append(res)
            

        #embd_x = (batch_size,n_fileds,embd_size)
        embd_x = torch.cat(results,dim=1)    #shape=(m,nf*k)
        embd_x = embd_x.view(batch_size,self.n_fields,self.embd_size) #shape=(m,nf,k)
        embd_x_ = embd_x.clone() # denotes E' in the paper
        
        input_x = embd_x.view(batch_size,1,self.n_fields,self.embd_size) #shape=(m,1,nf,k)
        
        p1,r1 = self.conv1(input_x)
        p2,r2 = self.conv2(p1)
        p3,r3 = self.conv3(p2)
        
        #r1 = (batch_size,C_new*H/2^i,embd_size)
        new_features = torch.cat([r1,r2,r3],dim=1)
        
        combine_features = torch.cat([embd_x,new_features],dim=1)
        
        #输入nf_16
        #则获得N=16+8+4=28
        #combine_features = (batch_size,N+n_f,embd_size)=(bz,28+16,40)=(bz,44,40)
        
        #inner product,fmlayer
        tmps = []
        for b in range(batch_size):
            results=[]
            for i in range(combine_features.shape[1]-1):
                for j in range(i+1,combine_features.shape[1]):
                        res = combine_features[b,i,:].view(1,-1).mm(combine_features[b,j,:].view(-1,1))
                        results.append(res) #(1,1)
            
            tmp = torch.cat(results,dim=1) #  [1,(N+nf)*(N+nf-1)/2]
            tmps.append(tmp)
        
        inner_producted = torch.cat(tmps,dim=0)  #[batch_size,(N+nf)*(N+nf-1)/2] =(bz,946)
        
        #flatten E'
        #inpt1 = [batch_size,(N+nf)*(N+nf-1)/2+nf*embd_size] =(bz,946+16*40)=(bz,1586)
        inp1= torch.cat([inner_producted,embd_x_.view(batch_size,-1)],dim=1) 
        
        #out=(bz,1)
        out = self.mlp(inp1)
        
        loss = self.loss_fn(out,true_y)
        
        return loss