OpenJ_Bailian - 7622：求排列的逆序数

011:求排列的逆序数

总Time Limit: 1000ms Memory Limit: 65536kB

Description
在Internet上的搜索引擎经常需要对信息进行比较，
比如可以通过某个人对一些事物的排名来估计他（或她）对各种不同信息的兴趣，从而实现个性化的服务。

对于不同的排名结果可以用逆序来评价它们之间的差异。
考虑1,2,…,n的排列i1，i2，…，in，如果其中存在j,k，满足 j < k 且 ij > ik， 那么就称(ij,ik)是这个排列的一个逆序。

一个排列含有逆序的个数称为这个排列的逆序数。
例如排列 263451 含有8个逆序(2,1),(6,3),(6,4),(6,5),(6,1),(3,1),(4,1),(5,1)，因此该排列的逆序数就是8。
显然，由1,2,…,n 构成的所有n!个排列中，最小的逆序数是0，
对应的排列就是1,2,…,n；最大的逆序数是n(n-1)/2，对应的排列就是n,(n-1),…,2,1。
逆序数越大的排列与原始排列的差异度就越大。

现给定1,2,…,n的一个排列，求它的逆序数。

Input
第一行是一个整数n，表示该排列有n个数（n <= 100000)。
第二行是n个不同的正整数，之间以空格隔开，表示该排列。

Output
输出该排列的逆序数。

Sample Input
6
2 6 3 4 5 1

Sample Output
8

Hint
1. 利用二分归并排序算法（分治）；
2. 注意结果可能超过int的范围，需要用long long存储。

解题思路：
    笨办法：O(n2)
    分治O(nlogn)：
        1） 将数组分成两半，分别求出左半边的逆序数和右半边的逆序数
        2） 再算有多少逆序是由左半边取一个数和右半边取一个数构成(要求O(n)实 现）
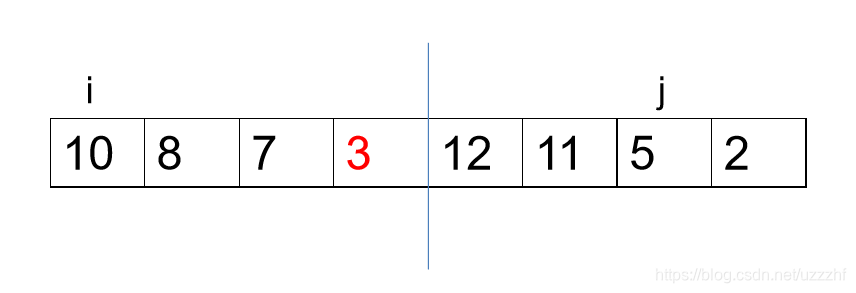
            2) 的关键：左半边和右半边都是排好序的。
            比如，都是从大到小排序的。
            这样，左右半边只需要从头到尾各扫一遍，就可以找出由两边各取一个数构成的逆序个数

            

#include <iostream>
#include <cstdio>
#define p 100001
using namespace std;

int a[p]; //源空间
int b[p]; //辅助空间
long long cnt=0;

void MergeNum(int s,int m,int e){
    int pb=s; //指向源空间
    int p1=s,p2=m+1; //分别指向两段空间的首地址

    while(p1 <= m && p2 <= e)
    {
        if(a[p1] > a[p2]) //从大到小排序
        {
            b[pb++]=a[p1++];
            cnt += e+1-p2;
        }
        else
            b[pb++]=a[p2++];
    }
    while(p1<=m)//说明左半部分还有剩下的元素，因为排好序了，就直接放入数组中即可
        b[pb++]=a[p1++];
    while(p2<=e)//说明右半部分还有剩下的元素，因为排好序了，就直接放入数组中即可
        b[pb++]=a[p2++];
    for(int i=s;i<=e;i++)//将a[]进行排序
        a[i]=b[i];
}

void MergeSortAndCount(int s,int e){
    if(s < e)
    {
        int m = s + (e-s)/2;//有效的避免了数据溢出问题
        MergeSortAndCount(s,m);//对前一半进行归并排序并计算逆序数
        MergeSortAndCount(m+1,e);//对后一半进行归并排序并计算逆序数
        MergeNum(s,m,e);//将这两半合起来计算逆序数
    }

}

int main()
{
    int n;
    scanf("%d",&n);
    for(int i=0; i<n ;++i)
        scanf("%d",&a[i]);
    MergeSortAndCount(0,n-1);
    printf("%lld\n",cnt);
}

 

#include <iostream>
#include <cstdio>
#define p 100001
using namespace std;

int a[p]; //源空间
int b[p]; //辅助空间
long long cnt=0;

void MergeNum(int s,int m,int e){
    int pb=s; //指向源空间
    int p1=s,p2=m+1; //分别指向两段空间的首地址

    while(p1 <= m && p2 <= e)
    {
        if(a[p1] < a[p2]) //从小到大排序
            b[pb++]=a[p1++];
        else
        {
            b[pb++]=a[p2++];
            cnt += m+1 - p1;//因为两部分已经排好序，若前半部分的a[i]已经大于a[j]了，则a[j]后面到a[m]都将大于a[j]
        }
    }
    while(p1<=m)//说明左半部分还有剩下的元素，因为排好序了，就直接放入数组中即可
        b[pb++]=a[p1++];
    while(p2<=e)//说明右半部分还有剩下的元素，因为排好序了，就直接放入数组中即可
        b[pb++]=a[p2++];
    for(int i=s;i<=e;i++)//将a[]进行排序
        a[i]=b[i];
}

void MergeSortAndCount(int s,int e){
    if(s < e)
    {
        int m = s + (e-s)/2;//有效的避免了数据溢出问题
        MergeSortAndCount(s,m);//对前一半进行归并排序并计算逆序数
        MergeSortAndCount(m+1,e);//对后一半进行归并排序并计算逆序数
        MergeNum(s,m,e);//将这两半合起来计算逆序数
    }

}

int main()
{
    int n;
    scanf("%d",&n);
    for(int i=0; i<n ;++i)
        scanf("%d",&a[i]);
    MergeSortAndCount(0,n-1);
    printf("%lld\n",cnt);
}