【LeetCode经典题解】二叉树层序遍历：从思路拆解到代码实现，手把手教你搞定！

最新推荐文章于 2026-01-08 21:36:59 发布

原创最新推荐文章于 2026-01-08 21:36:59 发布 · 995 阅读

74 ·

CC 4.0 BY-SA版权

文章标签：

#leetcode #算法 #职场和发展

Java.数据结构专栏收录该内容

18 篇文章

订阅专栏

在这里插入图片描述

🎁个人主页：User_芊芊君子
🎉欢迎大家点赞👍评论📝收藏⭐文章
🔍系列专栏：Java.数据结构

在这里插入图片描述

【前言】

二叉树的层序遍历是面试高频考点之一，它要求“逐层、从左到右”访问树的所有节点，最终返回每层节点值组成的二维列表。本文将通过一段代码，图文并茂的方式拆解其实现思路与核心逻辑。

一、二叉树层序遍历

二叉树层序遍历遵循“从上到下，从左到右”的原则访问树的所有节点，然后返回二维数组列表
在这里插入图片描述

二、思路分析

队列 + 分层循环

1.初始化“容器”

定义二维数组列表：List<List<Character>> ret = new ArrayList<>();
存储每层节点组成的列表；

2.空树处理：

判断跟是否为空，为空就直接返回ret

3.辅助：队列

队列先进先出的原则符合层序遍历从上到下，从左到右的访问顺序
Queue<TreeNode> queue = new LinkedList<>();
先将根节点入队

4.循环逻辑处理

4.1 外层循环

队列只要不为空，就一直访问每个节点，直到全部处理完成

4.2 内层循环

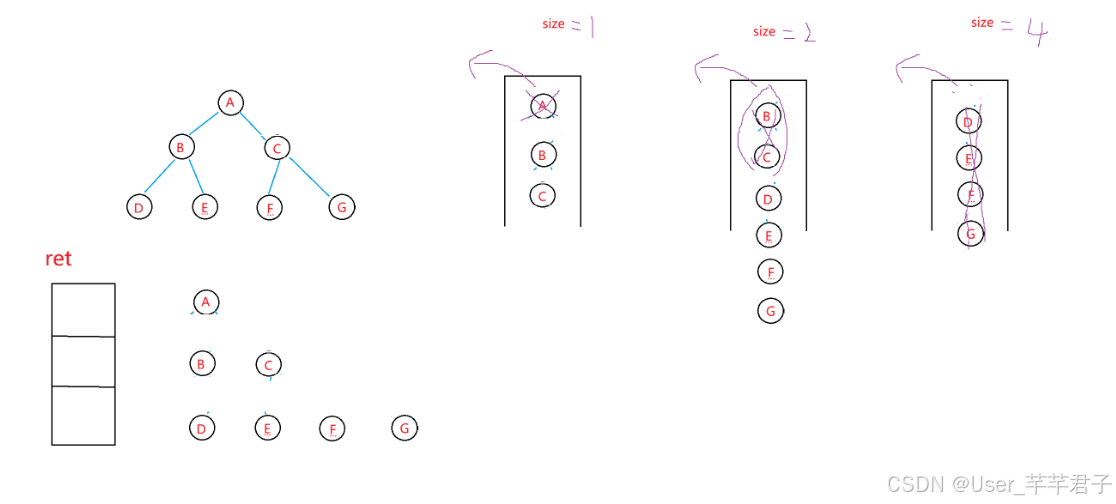
创建当前层容器: List<Character> curRow = new ArrayList<>();存储每层节点
固定当前层节点数:int size = queue.size();获取队列当前长度
(size可以确保当前层不会混入其他节点，因为后面处理时，会将下一层的节点入队)
遍历当前每个节点

先出队:TreeNode cur = queue.poll();
然后存进当前层；
判断左右子节点是否为空，不为空就进队；
size–，直到当前层节点全部处理完成

在这里插入图片描述

三、代码展示

【注意】：注释详解

 public List<List<Character>> levelOrder(TreeNode root) {
        //创建二维数组列表：储存每层节点
        List<List<Character>> ret = new ArrayList<>();
        //空树处理
        if(root == null){
            return ret;
        }
        //创建队列
        Queue<TreeNode> queue = new LinkedList<>();
        //进队
        queue.offer(root);
        //外层循环：处理每一层
        while(!queue.isEmpty()){
            //当前层存储列表
            List<Character> curRow = new ArrayList<>();
            //当前层节点树
            int size = queue.size();
            //内层循环：处理当前层
            while(size != 0){
                //出队
                TreeNode cur = queue.poll();
                //存入当前层
                curRow.add(cur.val);
                if(cur.left != null){
                    queue.offer(cur.left);
                }
                if(cur.right != null){
                    queue.offer(cur.right);
                }
                size--;
            }
            //将当前层加入结果列表
            ret.add(curRow);
        }
        return ret;
    }

四、总结

本次博客围绕二叉树层序遍历展开，其核心是遵循“从上到下、从左到右”的遍历原则，通过“二维列表存结果、队列辅助控顺序、嵌套循环分层次”的思路实现：先初始化结果容器并处理空树边界，再以队列存储待遍历节点，最后通过外层循环控制层级、内层循环处理层内节点（借助 size 变量固定当前层节点数），完成每层节点值的收集；这一实现不仅清晰完成了基础层序遍历，也为后续算法拓展提供了简洁框架，是二叉树广度优先遍历思路与实践结合的典型案例。

在这里插入图片描述