在大数据时代中,如何从海量数据中挖掘优质内容,算法成为有效规整和利用的一种常见应用手段。同时作为程序员修炼内功最直接的途径,就是深度学习和活用这强大的算法,所以让我们奔回曾经学习的起点,回溯这经典的排序算法。
诚然,我们能发现无论是算法书籍,还是论坛里面的优质文章,发现讲述经典排序算法还真不少。
所以我们还是进行汇总式学习吧!直接上总概览图理论性认识经典排序算法哈。
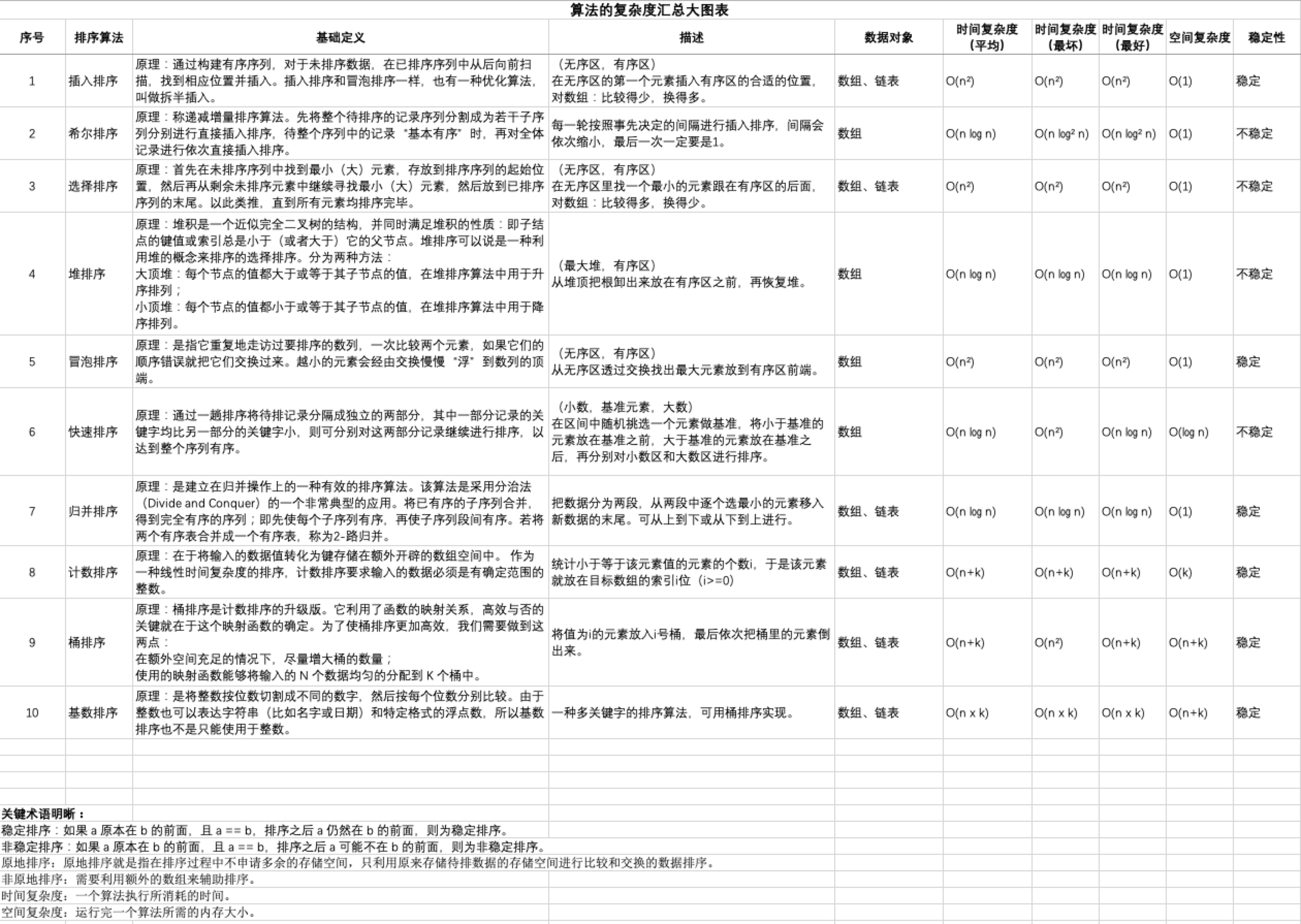
RUNOOB.COM 十大经典算法(里面包含多种编程语言的算法实现):
https://www.runoob.com/w3cnote/ten-sorting-algorithm.html
接着,跨越理论的认识,我们还是踏踏实实在引擎编辑中,进行排序算法的实战练习吧。
1、按照常规操作,新建UnitySortExample Unity3D项目,简单的配置我们直接略过,我们直奔核心算法逻辑类(C#)。
using
System
;
using
System
.
Collections
.
Generic
;
using
UnityEngine
;
/// <summary>
/// 排序逻辑控制器(参照:https://www.runoob.com/w3cnote/ten-sorting-algorithm.html)
/// </summary>
public
class
SortController
:
MonoBehaviour
{
private
static
SortController
_instance
;
public
static
SortController
GetInstance
(
)
{
return
_instance
;
}
void
Awake
(
)
{
if
(
_instance
==
null
)
{
_instance
=
this
;
DontDestroyOnLoad
(
gameObject
)
;
}
else
{
if
(
_instance
!=
this
)
{
Debug
.
Log
(
"warning: multiple Manager creating!"
)
;
GameObject
.
Destroy
(
gameObject
)
;
}
}
}
#
region
选择排序
/// <summary>
/// 选择排序
/// </summary>
/// <param name="arr">需要排序的数组值</param>
/// <returns></returns>
public
int
[
]
SelectSort
(
int
[
]
arr
)
{
int
n
=
arr
.
Length
;
for
(
int
i
=
0
;
i
<
n
-
1
;
i
++
)
{
int
min
=
i
;
for
(
int
j
=
i
+
1
;
j
<
n
;
j
++
)
{
if
(
arr
[
min
]
>
arr
[
j
]
)
min
=
j
;
}
//交换
int
temp
=
arr
[
i
]
;
arr
[
i
]
=
arr
[
min
]
;
arr
[
min
]
=
temp
;
}
return
arr
;
}
#
endregion
#
region
插入排序
/// <summary>
/// 插入排序
/// </summary>
/// <param name="arr">需要排序的数组值</param>
/// <returns></returns>
public
int
[
]
InsertSort
(
int
[
]
arr
)
{
if
(
arr
==
null
||
arr
.
Length
<
2
)
return
arr
;
int
n
=
arr
.
Length
;
for
(
int
i
=
1
;
i
<
n
;
i
++
)
{
int
temp
=
arr
[
i
]
;
int
k
=
i
-
1
;
while
(
k
>=
0
&&
arr
[
k
]
>
temp
)
k
--
;
//腾出位置插进去,要插的位置是 k + 1;
for
(
int
j
=
i
;
j
>
k
+
1
;
j
--
)
arr
[
j
]
=
arr
[
j
-
1
]
;
//插进去
arr
[
k
+
1
]
=
temp
;
}
return
arr
;
}
#
endregion
#
region
冒泡排序
/// <summary>
/// 冒泡排序
/// </summary>
/// <param name="arr">需要排序的数组值</param>
/// <returns></returns>
public
int
[
]
BubbleSort
(
int
[
]
arr
)
{
if
(
arr
==
null
||
arr
.
Length
<
2
)
{
return
arr
;
}
int
n
=
arr
.
Length
;
for
(
int
i
=
0
;
i
<
n
;
i
++
)
{
for
(
int
j
=
0
;
j
<
n
-
i
-
1
;
j
++
)
{
if
(
arr
[
j
+
1
]
<
arr
[
j
]
)
{
int
t
=
arr
[
j
]
;
arr
[
j
]
=
arr
[
j
+
1
]
;
arr
[
j
+
1
]
=
t
;
}
}
}
return
arr
;
}
#
endregion
#
region
希尔排序
/// <summary>
/// 希尔排序
/// </summary>
/// <param name="arr">需要排序的数组值</param>
/// <returns></returns>
public
int
[
]
ShellSort
(
int
[
]
arr
)
{
if
(
arr
==
null
||
arr
.
Length
<
2
)
return
arr
;
int
n
=
arr
.
Length
;
// 对每组间隔为 h的分组进行排序,刚开始 h = n / 2;
for
(
int
h
=
n
/
2
;
h
>
0
;
h
/=
2
)
{
//对各个局部分组进行插入排序
for
(
int
i
=
h
;
i
<
n
;
i
++
)
{
// 将arr[i] 插入到所在分组的正确位置上
InsertIValue
(
arr
,
h
,
i
)
;
}
}
return
arr
;
}
/// <summary>
/// 将arr[i]插入到所在分组的正确位置上,arr[i]] 所在的分组为 ... arr[i-2*h],arr[i-h], arr[i+h] ...
/// </summary>
/// <param name="arr"></param>
/// <param name="h"></param>
/// <param name="i"></param>
private
void
InsertIValue
(
int
[
]
arr
,
int
h
,
int
i
)
{
int
temp
=
arr
[
i
]
;
int
k
;
for
(
k
=
i
-
h
;
k
>
0
&&
temp
<
arr
[
k
]
;
k
-=
h
)
{
arr
[
k
+
h
]
=
arr
[
k
]
;
}
arr
[
k
+
h
]
=
temp
;
}
#
endregion
#
region
归并排序
/// <summary>
/// 归并排序(递归式)
/// </summary>
/// <param name="arr">需要排序的数组值</param>
/// <param name="left">左半部分索引</param>
/// <param name="right">右半部分索引</param>
/// <returns></returns>
public
int
[
]
MergeSort
(
int
[
]
arr
,
int
left
,
int
right
)
{
// 如果 left == right,表示数组只有一个元素,则不用递归排序
if
(
left
<
right
)
{
// 把大的数组分隔成两个数组
int
mid
=
(
left
+
right
)
/
2
;
// 对左半部分进行排序
arr
=
MergeSort
(
arr
,
left
,
mid
)
;
// 对右半部分进行排序
arr
=
MergeSort
(
arr
,
mid
+
1
,
right
)
;
//进行合并
Merge
(
arr
,
left
,
mid
,
right
)
;
}
return
arr
;
}
/// <summary>
/// 归并排序(非递归式)
/// </summary>
/// <param name="arr"></param>
/// <returns></returns>
public
int
[
]
MergeNonFuncSort
(
int
[
]
arr
)
{
int
n
=
arr
.
Length
;
//子数组的大小分别为1,2,4,8...,合并的数组大小是1,接着是2,接着4...
for
(
int
i
=
1
;
i
<
n
;
i
+=
i
)
{
//进行数组进行划分
int
left
=
0
;
int
mid
=
left
+
i
-
1
;
int
right
=
mid
+
i
;
//进行合并,对数组大小为 i 的数组进行两两合并
while
(
right
<
n
)
{
//合并函数和递归式的合并函数一样
Merge
(
arr
,
left
,
mid
,
right
)
;
left
=
right
+
1
;
mid
=
left
+
i
-
1
;
right
=
mid
+
i
;
}
// 剩余数组合并
if
(
left
<
n
&&
mid
<
n
)
{
Merge
(
arr
,
left
,
mid
,
n
-
1
)
;
}
}
return
arr
;
}
/// <summary>
/// 合并函数,把两个有序的数组合并起来。arr[left..mif]表示一个数组,arr[mid+1 .. right]表示一个数组
/// </summary>
/// <param name="arr"></param>
/// <param name="left"></param>
/// <param name="mid"></param>
/// <param name="right"></param>
private
void
Merge
(
int
[
]
arr
,
int
left
,
int
mid
,
int
right
)
{
//临时数组进行合并汇总
int
[
]
a
=
new
int
[
right
-
left
+
1
]
;
int
i
=
left
;
int
j
=
mid
+
1
;
int
k
=
0
;
while
(
i
<=
mid
&&
j
<=
right
)
{
if
(
arr
[
i
]
<
arr
[
j
]
)
{
a
[
k
++
]
=
arr
[
i
++
]
;
}
else
{
a
[
k
++
]
=
arr
[
j
++
]
;
}
}
while
(
i
<=
mid
)
a
[
k
++
]
=
arr
[
i
++
]
;
while
(
j
<=
right
)
a
[
k
++
]
=
arr
[
j
++
]
;
//临时数组复制到原数组
for
(
i
=
0
;
i
<
k
;
i
++
)
{
arr
[
left
++
]
=
a
[
i
]
;
}
}
#
endregion
#
region
快速排序
/// <summary>
/// 快速排序
/// </summary>
/// <param name="arr">需要排序的数组值</param>
/// <param name="left"></param>
/// <param name="right"></param>
/// <returns></returns>
public
int
[
]
QuickSort
(
int
[
]
arr
,
int
left
,
int
right
)
{
if
(
left
<
right
)
{
//获取中轴元素所处的位置
int
mid
=
PartPosition
(
arr
,
left
,
right
)
;
//进行分割
arr
=
QuickSort
(
arr
,
left
,
mid
-
1
)
;
arr
=
QuickSort
(
arr
,
mid
+
1
,
right
)
;
}
return
arr
;
}
/// <summary>
/// 获取中轴元素所处的位置
/// </summary>
/// <param name="arr"></param>
/// <param name="left"></param>
/// <param name="right"></param>
/// <returns></returns>
private
int
PartPosition
(
int
[
]
arr
,
int
left
,
int
right
)
{
//选取中轴元素
int
pivot
=
arr
[
left
]
;
int
i
=
left
+
1
;
int
j
=
right
;
while
(
true
)
{
// 向右找到第一个小于等于 pivot 的元素位置
while
(
i
<=
j
&&
arr
[
i
]
<=
pivot
)
i
++
;
// 向左找到第一个大于等于 pivot 的元素位置
while
(
i
<=
j
&&
arr
[
j
]
>=
pivot
)
j
--
;
if
(
i
>=
j
)
break
;
//交换两个元素的位置,使得左边的元素不大于pivot,右边的不小于pivot
int
temp
=
arr
[
i
]
;
arr
[
i
]
=
arr
[
j
]
;
arr
[
j
]
=
temp
;
}
arr
[
left
]
=
arr
[
j
]
;
// 使中轴元素处于有序的位置
arr
[
j
]
=
pivot
;
return
j
;
}
#
endregion
#
region
堆排序
/// <summary>
/// 堆排序
/// </summary>
/// <param name="arr"></param>
/// <returns></returns>
public
int
[
]
HeadSort
(
int
[
]
arr
)
{
int
n
=
arr
.
Length
;
//构建大顶堆
for
(
int
i
=
(
n
-
2
)
/
2
;
i
>=
0
;
i
--
)
{
DownAdjust
(
arr
,
i
,
n
-
1
)
;
}
//进行堆排序
for
(
int
i
=
n
-
1
;
i
>=
1
;
i
--
)
{
// 把堆顶元素与最后一个元素交换
int
temp
=
arr
[
i
]
;
arr
[
i
]
=
arr
[
0
]
;
arr
[
0
]
=
temp
;
// 把打乱的堆进行调整,恢复堆的特性
DownAdjust
(
arr
,
0
,
i
-
1
)
;
}
return
arr
;
}
/// <summary>
/// 下沉操作
/// </summary>
/// <param name="arr"></param>
/// <param name="parent"></param>
/// <param name="n"></param>
public
void
DownAdjust
(
int
[
]
arr
,
int
parent
,
int
n
)
{
//临时保存要下沉的元素
int
temp
=
arr
[
parent
]
;
//定位左孩子节点的位置
int
child
=
2
*
parent
+
1
;
//开始下沉
while
(
child
<=
n
)
{
// 如果右孩子节点比左孩子大,则定位到右孩子
if
(
child
+
1
<=
n
&&
arr
[
child
]
<
arr
[
child
+
1
]
)
child
++
;
// 如果孩子节点小于或等于父节点,则下沉结束
if
(
arr
[
child
]
<=
temp
)
break
;
// 父节点进行下沉
arr
[
parent
]
=
arr
[
child
]
;
parent
=
child
;
child
=
2
*
parent
+
1
;
}
arr
[
parent
]
=
temp
;
}
#
endregion
#
region
计算排序
/// <summary>
/// 计算排序
/// </summary>
/// <param name="arr"></param>
/// <returns></returns>
public
int
[
]
CountSort
(
int
[
]
arr
)
{
if
(
arr
==
null
||
arr
.
Length
<
2
)
return
arr
;
int
n
=
arr
.
Length
;
int
min
=
arr
[
0
]
;
int
max
=
arr
[
0
]
;
// 寻找数组的最大值与最小值
for
(
int
i
=
1
;
i
<
n
;
i
++
)
{
if
(
max
<
arr
[
i
]
)
max
=
arr
[
i
]
;
if
(
min
>
arr
[
i
]
)
min
=
arr
[
i
]
;
}
int
d
=
max
-
min
+
1
;
//创建大小为max的临时数组
int
[
]
temp
=
new
int
[
d
]
;
//统计元素i出现的次数
for
(
int
i
=
0
;
i
<
n
;
i
++
)
{
temp
[
arr
[
i
]
-
min
]
++
;
}
int
k
=
0
;
//把临时数组统计好的数据汇总到原数组
for
(
int
i
=
0
;
i
<
d
;
i
++
)
{
for
(
int
j
=
temp
[
i
]
;
j
>
0
;
j
--
)
{
arr
[
k
++
]
=
i
+
min
;
}
}
return
arr
;
}
#
endregion
#
region
桶排序
/// <summary>
/// 桶排序
/// </summary>
/// <param name="arr"></param>
/// <param name="bucketNum"></param>
public
double
[
]
BucketSort
(
double
[
]
arr
,
int
bucketNum
)
{
//创建bucket时,在二维中增加一组标识位,其中bucket[x, 0]表示这一维所包含的数字的个数
//通过这样的技巧可以少写很多代码
double
[
,
]
bucket
=
new
double
[
bucketNum
,
arr
.
Length
+
1
]
;
foreach
(
var
num
in
arr
)
{
int
bit
=
(
int
)
(
bucketNum
*
num
)
;
bucket
[
bit
,
(
int
)
++
bucket
[
bit
,
0
]
]
=
num
;
}
//为桶里的每一行使用插入排序
for
(
int
j
=
0
;
j
<
bucketNum
;
j
++
)
{
//为桶里的行创建新的数组后使用插入排序
double
[
]
insertion
=
new
double
[
(
int
)
bucket
[
j
,
0
]
]
;
for
(
int
k
=
0
;
k
<
insertion
.
Length
;
k
++
)
{
insertion
[
k
]
=
bucket
[
j
,
k
+
1
]
;
}
//调用插入排序
StraightInsertionSort
(
insertion
)
;
//把排好序的结果回写到桶里
for
(
int
k
=
0
;
k
<
insertion
.
Length
;
k
++
)
{
bucket
[
j
,
k
+
1
]
=
insertion
[
k
]
;
}
}
//将所有桶里的数据回写到原数组中
for
(
int
count
=
0
,
j
=
0
;
j
<
bucketNum
;
j
++
)
{
for
(
int
k
=
1
;
k
<=
bucket
[
j
,
0
]
;
k
++
)
{
arr
[
count
++
]
=
bucket
[
j
,
k
]
;
}
}
return
arr
;
}
private
void
StraightInsertionSort
(
double
[
]
array
)
{
//插入排序
for
(
int
i
=
1
;
i
<
array
.
Length
;
i
++
)
{
double
sentinel
=
array
[
i
]
;
int
j
=
i
-
1
;
while
(
j
>=
0
&&
sentinel
<
array
[
j
]
)
{
array
[
j
+
1
]
=
array
[
j
]
;
j
--
;
}
array
[
j
+
1
]
=
sentinel
;
}
}
#
endregion
#
region
基数排序
/// <summary>
/// 基数排序
/// </summary>
/// <param name="myArray"></param>
/// <param name="keyNum"></param>
public
int
[
]
RandixSort
(
int
[
]
myArray
,
int
keyNum
)
{
SingleLinkedList
<
int
>
listArray
=
new
SingleLinkedList
<
int
>
(
)
;
foreach
(
int
i
in
myArray
)
{
listArray
.
AddLast
(
new
SingleLLNode
<
int
>
(
)
{
Value
=
i
}
)
;
}
for
(
int
i
=
0
;
i
<
keyNum
;
i
++
)
{
// 对每个关键字执行分配和收集操作
DistributeAndCollect
(
listArray
,
i
)
;
}
int
j
=
0
;
while
(
listArray
.
First
!=
null
)
{
myArray
[
j
++
]
=
listArray
.
First
.
Value
;
listArray
.
First
=
listArray
.
First
.
Next
;
}
return
myArray
;
}
/// <summary>
/// 分配和收集
/// </summary>
/// <param name="listArray"></param>
/// <param name="i"></param>
private
void
DistributeAndCollect
(
SingleLinkedList
<
int
>
listArray
,
int
i
)
{
int
randix
=
10
;
//关键字取值范围
int
divider
=
(
int
)
Math
.
Pow
(
10
,
i
)
;
List
<
SingleLinkedList
<
int
>
>
subLists
=
new
List
<
SingleLinkedList
<
int
>
>
(
)
;
//建立子序列
for
(
int
j
=
0
;
j
<
randix
;
j
++
)
{
subLists
.
Add
(
new
SingleLinkedList
<
int
>
(
)
)
;
}
// 开始一次分配
while
(
listArray
.
First
!=
null
)
{
int
index
=
(
listArray
.
First
.
Value
/
divider
)
%
10
;
SingleLLNode
<
int
>
tempNode
=
listArray
.
First
.
Next
;
subLists
[
index
]
.
AddLast
(
listArray
.
First
)
;
listArray
.
First
=
tempNode
;
}
// 开始一次收集
int
k
=
0
;
for
(
;
k
<
randix
;
k
++
)
{
if
(
subLists
[
k
]
.
First
!=
null
)
{
// 找到第一个非空子序列以设置总序列的First值
listArray
.
First
=
subLists
[
k
]
.
First
;
listArray
.
Last
=
subLists
[
k
]
.
Last
;
break
;
}
}
// 找好子序列设置好listArray.First后,开始处理非空子序列的首尾相连
for
(
;
k
<
randix
;
k
++
)
{
if
(
subLists
[
k
]
.
First
!=
null
)
{
listArray
.
Last
.
Next
=
subLists
[
k
]
.
First
;
listArray
.
Last
=
subLists
[
k
]
.
Last
;
}
}
}
#
endregion
}
// 单链表
class
SingleLinkedList
<
T
>
{
public
SingleLLNode
<
T
>
First
{
get
;
set
;
}
public
SingleLLNode
<
T
>
Last
{
get
;
set
;
}
public
void
AddLast
(
SingleLLNode
<
T
>
node
)
{
if
(
First
==
null
)
{
First
=
node
;
Last
=
node
;
node
.
Next
=
null
;
}
else
{
Last
.
Next
=
node
;
Last
=
node
;
node
.
Next
=
null
;
}
}
}
// 单链表结点
class
SingleLLNode
<
T
>
{
public
T
Value
{
get
;
set
;
}
public
SingleLLNode
<
T
>
Next
{
get
;
set
;
}
}
2、结合简单UI的展示,运行预览测试。
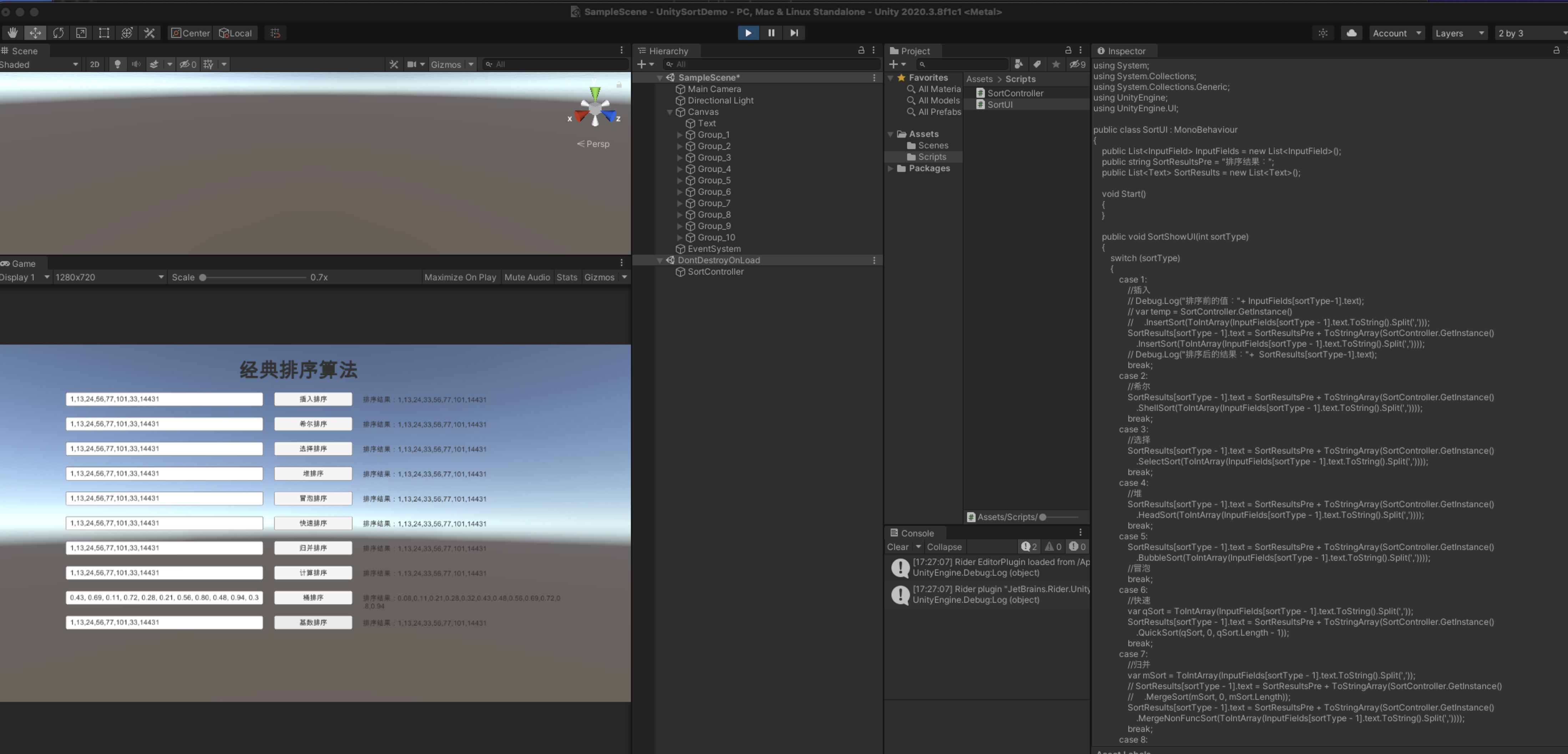
相关实战练习工程已直接上传在Github上,感兴趣的小伙伴可以下载一起学习哈。
最后,小编还想推荐一些三方有关算法的分享(感兴趣的可以直接Mark下哈):
1、使用C#和Windows窗体应用程序实现的排序可视化工具:
https://github.com/haltaf19/Sorting-Visualizer
2、 排序算法可视化,使用Unity实现的排序算法演示系统:
https://github.com/ChengziCao/sorting-visualization
3、基于Unity简单地实现游戏程序开发中常用的算法:
https://github.com/IceLanguage/LinHowe_GameAlgorithm
4、Unity中的地形拓扑算法:
https://github.com/Scrawk/Terrain-Topology-Algorithms
5、BFS、贪婪最佳优先搜索、Dijkstra和A*路径查找算法:
https://github.com/dbrizov/Unity-PathFindingAlgorithms
6、基于遗传进化算法的Unity计算着色程序绘制算法:
https://github.com/IRCSS/Procedural-painting
7、Teddy算法(将二维多边形转换为三维模型)在Unity中的实现:
https://github.com/mattatz/unity-teddy




 本文介绍并实现了十种经典排序算法,包括选择排序、插入排序、冒泡排序等,并提供了Unity项目的实战示例。
本文介绍并实现了十种经典排序算法,包括选择排序、插入排序、冒泡排序等,并提供了Unity项目的实战示例。
















 3148
3148

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








