本文深入解析决策树模型，包括ID3、C4.5、CART等算法的原理与差异，探讨信息增益、基尼指数等启发函数，并介绍预剪枝与后剪枝两种决策树优化策略。
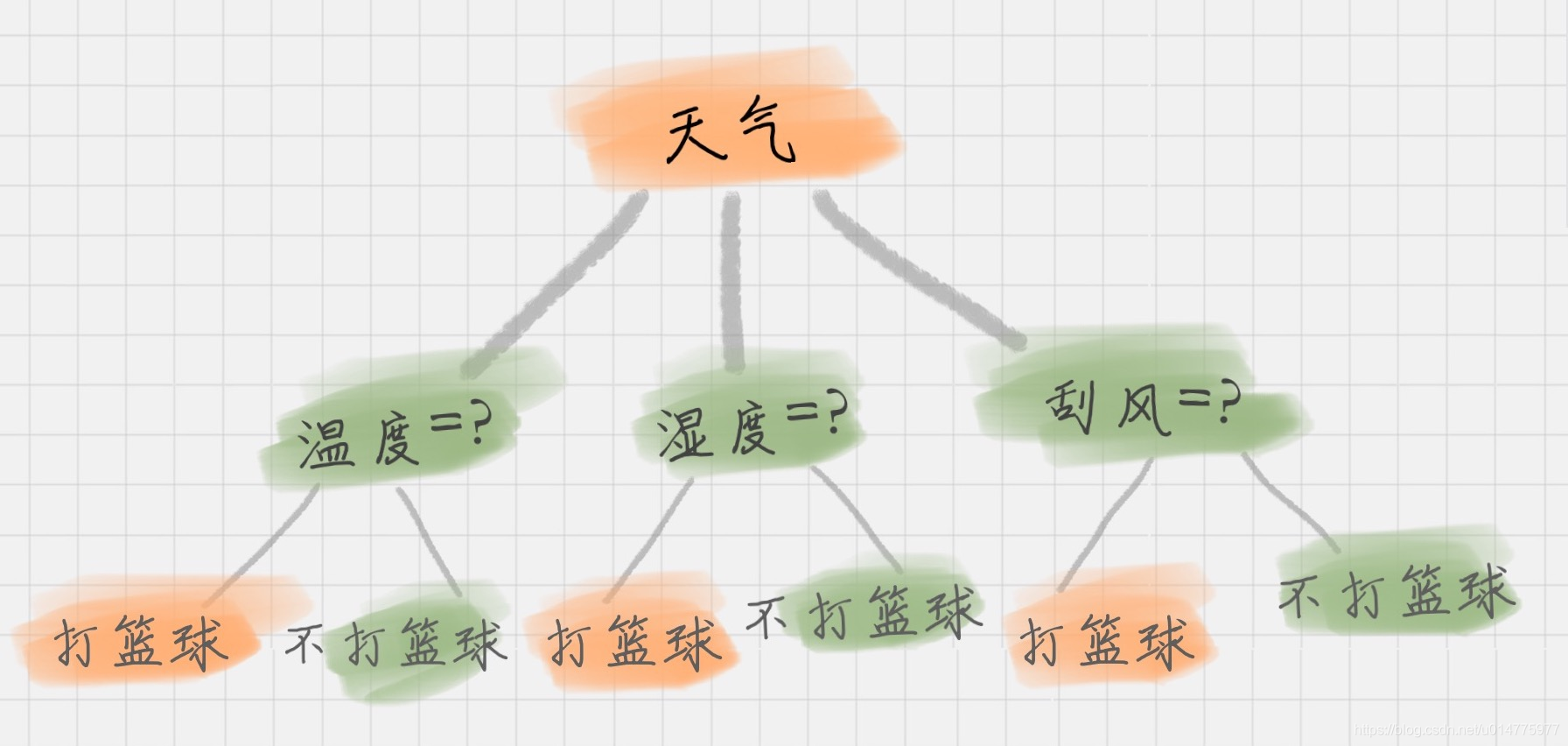
1.什么是决策树？
1. 决策树是一种自上而下，对样本数据进行树形分类的过程，由节点和有向边组成。
2. 决策树作为最基础、最常见的有监督学习模型，常被用于分类问题和回归问题，
3. 在市场营销和生物医药等领域尤其受欢迎，主要是因为树形结构与销售、诊断等场景下的决策过程非常相似，
4. 决策树具有简单直观、解释性强的优点。
2.决策树有哪些常用的启发函数？
一般而言，决策树的生成包含了特征选择、树的构造、树的剪枝三个过程。
从若干不同的决策树中选取最优的决策树是一个NP完全问题，
在实际中我们通常会采用启发式学习的方法去构建一颗满足启发式条件的决策树。
常用的决策树算法有：ID3、C4.5、CART，除了构建准则之外，它们之间的区别和联系是什么？
2.1 ——ID3-最大信息增益
-
经验熵
对于样本集和DDD，类别数为KKK，数据集DDD的经验熵表示为H(D)=−∑k=1K∣Ck∣∣D∣log2∣Ck∣∣D∣H(D)=-\sum_{k=1}^{K}\frac{ |C_{k}|}{|D|} log_{2}\frac{|C_{k}|}{|D|} H(D)=−k=1∑K∣D∣∣Ck∣log2∣D∣∣Ck∣
其中，CkC_{k}Ck是样本集合DDD中属于第kkk类的样本子集，∣Ck∣|C_{k}|∣Ck∣表示为该子集的元素个数，∣D∣|D|∣D∣表示样本集和的元素个数。 -
经验条件熵
某个特征AAA对于数据集DDD的经验条件熵H(D∣A)H(D|A)H(D∣A)为
H(D∣A)=∑i=1k∣Di∣∣D∣H(Di)=∑i=1n∣Di∣∣D∣⟮−∑k=1k∣Dik∣∣Di∣log2∣Dik∣∣Di∣⟯ H(D|A)= \sum_{i=1}^{k} \frac{|D_{i}|}{|D|}H(D_{i}) = \sum_{i=1}^{n} \frac{|D_{i}|}{|D|} \lgroup -\sum_{k=1}^{k}\frac{ |D_{ik}|}{|D_{i}|} log_{2}\frac{|D_{ik}|}{|D_{i}|} \rgroup H(D∣A)=i=1∑k∣D∣∣Di∣H(Di)=i=1∑n∣D∣∣Di∣⟮−k=1∑k∣Di∣∣Dik∣log2∣Di∣∣Dik∣⟯
其中，DiD_{i}Di表示DDD中特征AAA取第iii个值的样本子集，DikD_{ik}Dik表示DiD_{i}Di中属于kkk类的样本子集。 -
信息增益
信息增益表示为两者之差，可得
g(D,A)=H(D)−H(D∣A)g(D,A)=H(D)-H(D|A) g(D,A)=H(D)−H(D∣A)
2.2 ——最大信息增益比
- 特征AAA对于数据集DDD的信息增益比定义为
gR(D,A)=g(D,A)HA(D) g_{R}(D,A) = \frac{g(D,A)}{H_{A}(D)} gR(D,A)=HA(D)g(D,A)
其中,HA(D)=−∑i=1nlog2∣Di∣∣D∣H_{A}(D)=-\sum_{i=1}^{n}log_{2} \frac{|D_{i}|}{|D|} HA(D)=−i=1∑nlog2∣D∣∣Di∣
称为数据集DDD关于AAA的取值熵。
2.3 ——CART-最大基尼指数（Gini）
- Gini描述的是数据的纯度，与信息熵含义类似
Gini(D)=1−∑k=1n⟮∣Ck∣∣D∣⟯2 Gini(D) = 1-\sum_{k=1}^{n} \lgroup \frac {|C_{k}|} {|D|} \rgroup^2 Gini(D)=1−k=1∑n⟮∣D∣∣Ck∣⟯2
CART在每一次迭代中选择基尼指数最小的特征及其对应的切分点进行分类。但与ID3、C4.5不同的是，CART是一颗二叉树，采用二元切割法，每一步将数据按特征AAA的取值分成两份，分别进入左右子树，特征AAA的Gini指数定义为
Gini(D∣A)=∑i=1n∣Di∣∣D∣Gini(Di) Gini(D|A)=\sum_{i=1}^{n}\frac {|D_{i}|}{|D|} Gini(D_{i}) Gini(D∣A)=i=1∑n∣D∣∣Di∣Gini(Di)
2.4——三者之间的对比差异
- ID3采用信息增益作为评价标准，会倾向选择取值较多的特征，信息增益反映的是给定条件以后不确定性减少的长度，特征取值越多就意味着确定性更高，也就是条件熵越小，信息增益越大。C4.5实际上是对ID3进行优化。
- ID3只能处理离散型变量，而C4.5和CART还能处理连续型变量。
- ID3和C4.5只能用于分类任务，而CART也可以应用回归任务（回归任务使用最小平方误差准则）
- ID3对样本缺失值比较敏感，而C4.5和CART可以对缺失值进行不同方式的处理
- ID3和C4.5可以在每个节点产生出多叉分支，且每个特征在层级之间不会复用，而CART在每个节点只会产生两个分支，因此最后形成一颗二叉树，且每个特征可以被重复利用
- ID3和C4.5通过剪枝来权衡树的准确性和泛化能力，而CART直接利用全部数据发现发现所有可能的树结构进行对比。
# 实现代码
import numpy as np
import pandas as pd
from collections import Counter
import math
class Node:
def __init__(self, x=None, label=None, y=None, data=None):
self.label = label # label:子节点分类依据的特征
self.x = x # x:特征
self.child = [] # child:子节点
self.y = y # y:类标记（叶节点才有）
self.data = data # data:包含数据（叶节点才有）
def append(self, node): # 添加子节点
self.child.append(node)
def predict(self, features): # 预测数据所述类
if self.y is not None:
return self.y
for c in self.child:
if c.x == features[self.label]:
return c.predict(features)
def printnode(node, depth=0): # 打印树所有节点
if node.label is None:
print(depth, (node.label, node.x, node.y, len(node.data)))
else:
print(depth, (node.label, node.x))
for c in node.child:
printnode(c, depth+1)
class DTree:
def __init__(self, epsilon=0, alpha=0): # 预剪枝、后剪枝参数
self.epsilon = epsilon
self.alpha = alpha
self.tree = Node()
def prob(self, datasets): # 求概率
datalen = len(datasets)
labelx = set(datasets)
p = {l: 0 for l in labelx}
for d in datasets:
p[d] += 1
for i in p.items():
p[i[0]] /= datalen
return p
def calc_ent(self, datasets): # 求熵
p = self.prob(datasets)
ent = sum([-v * math.log(v, 2) for v in p.values()])
return ent
def cond_ent(self, datasets, col): # 求条件熵
labelx = set(datasets.iloc[col])
p = {x: [] for x in labelx}
for i, d in enumerate(datasets.iloc[-1]):
p[datasets.iloc[col][i]].append(d)
return sum([self.prob(datasets.iloc[col])[k] * self.calc_ent(p[k]) for k in p.keys()])
def info_gain_train(self, datasets, datalabels): # 求信息增益（互信息）
#print('----信息增益----')
datasets = datasets.T
ent = self.calc_ent(datasets.iloc[-1])
gainmax = {}
for i in range(len(datasets) - 1):
cond = self.cond_ent(datasets, i)
#print(datalabels[i], ent - cond)
gainmax[ent - cond] = i
m = max(gainmax.keys())
return gainmax[m], m
def train(self, datasets, node):
labely = datasets.columns[-1]
if len(datasets[labely].value_counts()) == 1:
node.data = datasets[labely]
node.y = datasets[labely][0]
return
if len(datasets.columns[:-1]) == 0:
node.data = datasets[labely]
node.y = datasets[labely].value_counts().index[0]
return
gainmaxi, gainmax = self.info_gain_train(datasets, datasets.columns)
#print('选择特征：', gainmaxi)
if gainmax <= self.epsilon: # 若信息增益（互信息）为0意为输入特征x完全相同而标签y相反
node.data = datasets[labely]
node.y = datasets[labely].value_counts().index[0]
return
vc = datasets[datasets.columns[gainmaxi]].value_counts()
for Di in vc.index:
node.label = gainmaxi
child = Node(Di)
node.append(child)
new_datasets = pd.DataFrame([list(i) for i in datasets.values if i[gainmaxi]==Di], columns=datasets.columns)
self.train(new_datasets, child)
def fit(self, datasets):
self.train(datasets, self.tree)
def findleaf(self, node, leaf): # 找到所有叶节点
for t in node.child:
if t.y is not None:
leaf.append(t.data)
else:
for c in node.child:
self.findleaf(c, leaf)
def findfather(self, node, errormin):
if node.label is not None:
cy = [c.y for c in node.child]
if None not in cy: # 全是叶节点
childdata = []
for c in node.child:
for d in list(c.data):
childdata.append(d)
childcounter = Counter(childdata)
old_child = node.child # 剪枝前先拷贝一下
old_label = node.label
old_y = node.y
old_data = node.data
node.label = None # 剪枝
node.y = childcounter.most_common(1)[0][0]
node.data = childdata
error = self.c_error()
if error <= errormin: # 剪枝前后损失比较
errormin = error
return 1
else:
node.child = old_child # 剪枝效果不好，则复原
node.label = old_label
node.y = old_y
node.data = old_data
else:
re = 0
i = 0
while i < len(node.child):
if_re = self.findfather(node.child[i], errormin) # 若剪过枝，则其父节点要重新检测
if if_re == 1:
re = 1
elif if_re == 2:
i -= 1
i += 1
if re:
return 2
return 0
def c_error(self): # 求C(T)
leaf = []
self.findleaf(self.tree, leaf)
leafnum = [len(l) for l in leaf]
ent = [self.calc_ent(l) for l in leaf]
print("Ent:", ent)
error = self.alpha*len(leafnum)
for l, e in zip(leafnum, ent):
error += l*e
print("C(T):", error)
return error
def cut(self, alpha=0): # 剪枝
if alpha:
self.alpha = alpha
errormin = self.c_error()
self.findfather(self.tree, errormin)
datasets = np.array([['青年', '否', '否', '一般', '否'],
['青年', '否', '否', '好', '否'],
['青年', '是', '否', '好', '是'],
['青年', '是', '是', '一般', '是'],
['青年', '否', '否', '一般', '否'],
['中年', '否', '否', '一般', '否'],
['中年', '否', '否', '好', '否'],
['中年', '是', '是', '好', '是'],
['中年', '否', '是', '非常好', '是'],
['中年', '否', '是', '非常好', '是'],
['老年', '否', '是', '非常好', '是'],
['老年', '否', '是', '好', '是'],
['老年', '是', '否', '好', '是'],
['老年', '是', '否', '非常好', '是'],
['老年', '否', '否', '一般', '否'],
['青年', '否', '否', '一般', '是']]) # 在李航原始数据上多加了最后这行数据，以便体现剪枝效果
datalabels = np.array(['年龄', '有工作', '有自己的房子', '信贷情况', '类别'])
train_data = pd.DataFrame(datasets, columns=datalabels)
test_data = ['老年', '否', '否', '一般']
dt = DTree(epsilon=0) # 可修改epsilon查看预剪枝效果
dt.fit(train_data)
print('DTree:')
printnode(dt.tree)
y = dt.tree.predict(test_data)
print('result:', y)
dt.cut(alpha=0.5) # 可修改正则化参数alpha查看后剪枝效果
print('DTree:')
printnode(dt.tree)
y = dt.tree.predict(test_data)
print('result:', y)
4.如何对决策树进行剪枝？
决策树的剪枝通常有两种方法，预剪枝（Pre-Pruning）和后剪枝(Post_Pruning）
预剪枝，即在生成决策树的过程中提前停止树的增长，
后剪枝，则在已生成的过拟合决策树上进行剪枝，得到简化版的剪枝决策树。
那么这两种方法是如何进行的呢？它们又各有什么优缺点？
- 预剪枝
即在生成决策树的过程中提前停止树的增长 ，预剪枝对停止决策树有以下几种方法- 当树达到一定高度的时候，停止树的生长。
- 当到达当前节点的样本数量小于某个阈值的时候，停止树的生长。
- 计算每次分裂对测试集的准确度提升，当小于某个阈值的时候，不在继续扩展
- 后剪枝
- 在这里介绍CART数的剪枝策略–代价复杂剪枝
扫一扫
545
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
