线性代数--方程组的几何解释

二维方程求解

尝试利用线性代数解如下方程：

• 方程组：
  $$\{\begin{array}{l}2x-y=0\\ -x+2y=3\end{array}$$

• 对应矩阵(row picture)：
  $$\left[\begin{array}{cc}2& -1\\ -2& 2\end{array}\right]\ast \left[\begin{array}{c}x\\ y\end{array}\right]=\left[\begin{array}{c}0\\ 3\end{array}\right]$$

$$A\ast X=B$$

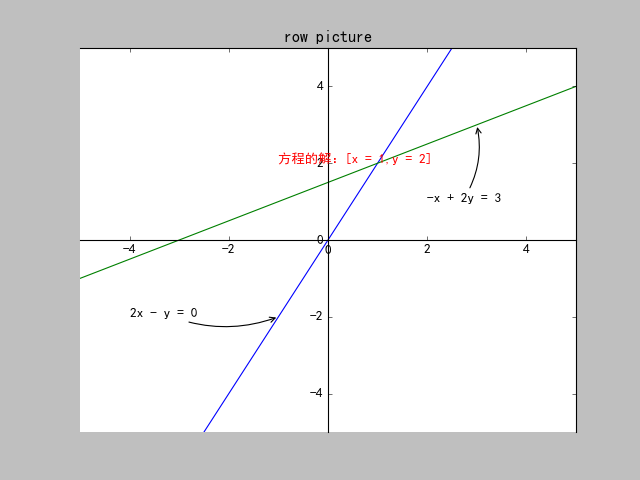
由上图可知，方程组的解为两线交点:
$$\{\begin{array}{l}x=1\\ y=2\end{array}$$

• 下面看对应的列图（column picture）:

$$x\ast \left[\begin{array}{c}2\\ -1\end{array}\right]+y\ast \left[\begin{array}{c}-1\\ 2\end{array}\right]=\left[\begin{array}{c}0\\ 3\end{array}\right]$$

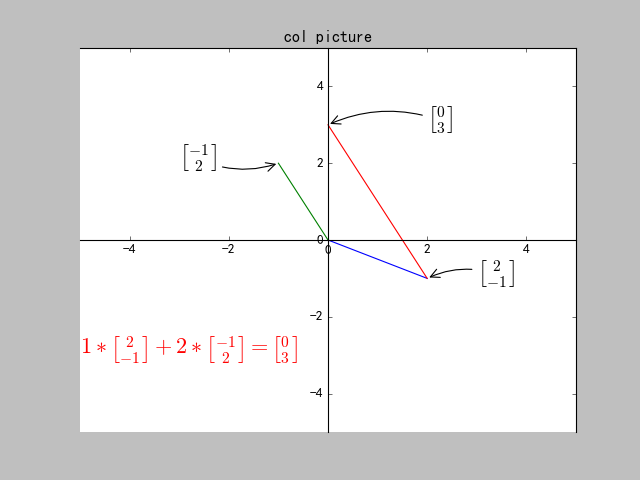
将由行图像的出的方程组解代入列图中:
$$1\ast \left[\begin{array}{c}2\\ -1\end{array}\right]+2\ast \left[\begin{array}{c}-1\\ 2\end{array}\right]=\left[\begin{array}{c}0\\ 3\end{array}\right]$$
显然，此方程成立。

列图像中可以看出其中1倍的向量（2，-1）加2倍的向量（-1，2）得到向量（0，3），其中（1，2）为方程某一个解。
所有如果求出方程所有可能的解，将会形成一个平面。请自行脑补，此平面形状

三维方程求解

• 方程组：
  $$\{\begin{array}{l}2x-y=0\\ -x+2y-z=-1\\ -3y+4z=4\end{array}$$
• 对应矩阵(row picture)：
  $$A=\left[\begin{array}{ccc}2& -1& 0\\ -1& 2& -1\\ 0& -3& 4\end{array}\right]b=\left[\begin{array}{c}0\\ -1\\ 4\end{array}\right]$$
  其行图像如下所示:
  

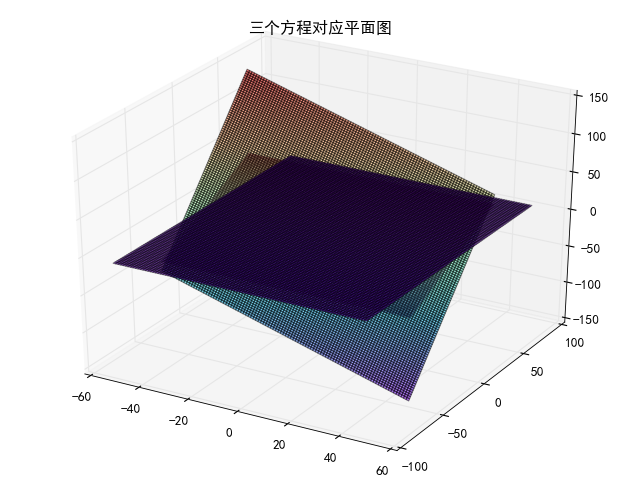
显然，从上图时无法肉眼看出此方程组的解，即无法看出三个平面相交与一点。二维方程绘图解法并不适用三维或更多维方程组求解。

• 列图像（column picture）

$$x\ast \left[\begin{array}{c}2\\ -1\\ 0\end{array}\right]+y\ast \left[\begin{array}{c}-1\\ 2\\ -3\end{array}\right]+z\ast \left[\begin{array}{c}0\\ -1\\ 4\end{array}\right]=\left[\begin{array}{c}0\\ -1\\ 4\end{array}\right]$$

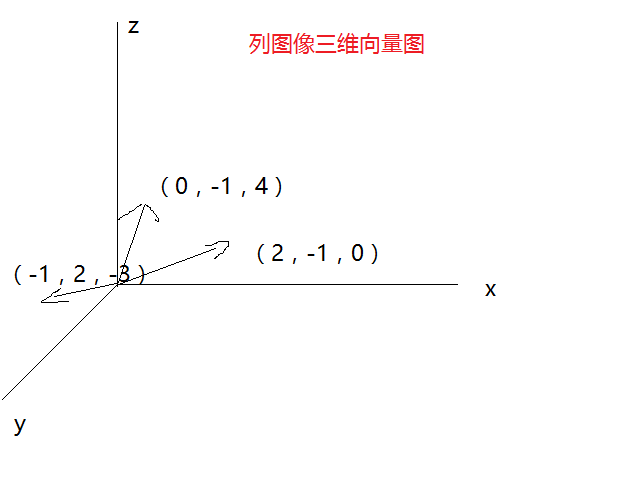
列图像中，同样虽无法直观求得方程的解，但清晰明了，某些情况下可以利用其求解，或是了解方程图像性质。
此例题答案很显然，其中b向量与z对应的向量相等，所以方程解之一如下：
$$\{\begin{array}{l}x=0\\ y=0\\ z=1\end{array}$$
x,y,z分别为左侧三个向量的分量，代入求得向量b

思考:
三维空间中，任意b,Ax=b是否都成立？
即什么情况下，三列向量无法通过组合得到b
或是，列的线性组合能否覆盖整个三维空间

矩阵乘法

以上示例都是基于矩阵乘以向量等于右侧向量的形式：
$$A\ast x=b$$
示例一(推荐)：
$$\left[\begin{array}{cc}2& 5\\ 1& 3\end{array}\right]\ast \left[\begin{array}{c}1\\ 2\end{array}\right]=1\ast \left[\begin{array}{c}2\\ 1\end{array}\right]+2\ast \left[\begin{array}{c}5\\ 3\end{array}\right]=\left[\begin{array}{c}12\\ 7\end{array}\right]$$

矩阵每一列分别乘以对应向量相加

示例二(点乘)：
$$\left[\begin{array}{cc}2& 5\\ 1& 3\end{array}\right]\ast \left[\begin{array}{c}1\\ 2\end{array}\right]=\left[\begin{array}{c}2\ast 1+5\ast 2\\ 1\ast 1+3\ast 2\end{array}\right]=\left[\begin{array}{c}12\\ 7\end{array}\right]$$

矩阵每一行都与向量进行点乘后相加