[Codeforces][976D] 图的构造 Educational Codeforces Round 43 (Rated for Div. 2) D. Degree Set

超喜欢这题的说

题目大意：给你一个正整数集，其中最大数为n，求构造一个图，使得有n+1个结点且这个图的结点的度组成的集合等于所给集合

这题在加里·查特兰所著的《图论----一个迷人的世界中》    出现在定理2.3.

不过这本书好像挺难找的

书上大意写了下，我看了半天马马虎虎理解，然后自己YY着想出了构造方法

构造图最有趣了

是这样的，我们假设要构造一个度集为{d}（d1<d2<d3<.....<dn），阶为dn+1的图

那么，我们可以进行以下操作：首先构造一个度集为{d2-d1,d3-d1,d4-d1,.....d(n-1)-d1},阶为d(n-1)-d1+1的图（称为S），然后构造一个d1阶完全图（Kd1），将Kd1中每一个点与S中每一个点连起来，然后做dn-d(n-1)个孤立点，将这些孤立点与Kd1一一对应相连即可。

举个例子：构造{2，3，5，6}    阶为7的图

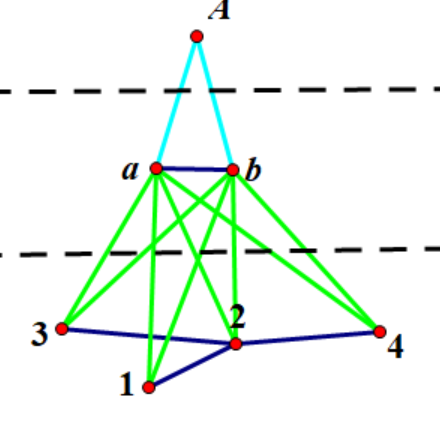这个图分为三个部分，分别是孤立点（A），完全图Kd1(a,b),和先前构造好的图S（1，2，3，4），然后Kd1和S，Kd1和孤立点两两相连即可构造出符合要求的图

于是这个问题就可以开始递归了。

那递归边界是什么？

当度集大小为1时，即整幅图只有一个度数d，则直接构造出一个d+1阶完全图即可

当度集大小为2时，可以把一个点拆成两个做。例如构造{1，2}的三阶图，就可以看成{1，1，2}的三阶图，然后三部分是1阶完全图，1个孤立点，一个一阶0度图即可，即A-a-1。

记得每次都要把d排序我就这样WA了好几次

上代码

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<algorithm>
#include<cstring>
#include<set>
#include<map>
#include<cmath>
#include<sstream>
#include<queue>
#include<vector>
#include<deque>
using namespace std;
typedef long long ll;
typedef vector<int> vi;
#define For(a,b,c) for (int (a)=(b);(a)<(c);(a)++)
#define foreach(iter,V) for (__typeof((V).begin()) iter=(V).begin();iter!=(V).end();iter++)
#define pb push_back
#define mp make_pair
#define fi first
#define se second
using namespace std;
int n,tot,len,siz;
vi d;
pair<int,int> ans[1000001];
vi K_(int x){
	vi res;
	For(i,0,x){
		siz++;
		res.pb(siz);
		For(j,1,i+1)	ans[++len]=mp(siz-j,siz); 
	}
	return res;
}
void debug(){
	
	cout<<len<<endl;
	For(i,1,len+1)	cout<<ans[i].fi<<" "<<ans[i].se<<endl;	
	cout<<endl;
}
vi construct(vi dd,int nn){
	sort(dd.begin(),dd.end());
	if (dd.size()==2){
		vi res;
		vi v=K_(dd[0]);
		siz++;
		res.pb(siz);
		For(i,0,v.size())	ans[++len]=mp(siz,v[i]);
		For(i,0,dd[1]-dd[0]){
			siz++;
			res.pb(siz);
			For(j,0,v.size())
				ans[++len]=mp(siz,v[j]);
		}
		For(i,0,v.size())	res.pb(v[i]);
		return res;	
	}
	if (dd.size()==1){
		vi res;
		res=K_(dd[0]+1);
		return res;
	}
	vi res;
	for (int i=dd.size()-2;i>0;i--)
		res.pb(dd[i]-dd[0]);
	res=construct(res,dd[dd.size()-2]-dd[0]+1);
	vi a=K_(dd[0]);
	vi an; 
	bool vis[10001];
	For(i,0,a.size())
		For(j,0,res.size()){
			ans[++len]=mp(a[i],res[j]);
			if (!vis[a[i]]){
				an.pb(a[i]);
				vis[a[i]]=1;
			}
			if (!vis[res[j]]){
				vis[res[j]]=1;
				an.pb(res[j]);	
			}
		}
	For(i,0,dd[dd.size()-1]-dd[dd.size()-2]){
		siz++;
		an.pb(siz);
		For(j,0,a.size())
			ans[++len]=mp(siz,a[j]); 
	}
	return an;
}
int main(){
	scanf("%d",&n);
	For(i,1,n+1)	scanf("%d",&tot),d.pb(tot);
	construct(d,d[d.size()-1]+1);
	cout<<len<<endl;
	For(i,1,len+1)	cout<<ans[i].fi<<" "<<ans[i].se<<endl;	
	return 0;
}