题目:房间有金子, 价值各不同。 连偷会报警, 如何赚大钱?
输入:houses = {3, 5, 2, 10}
解释:有四间屋子,金子的价值各是3、5、2、10 偷的时候,不能偷连续的房间,
比如,偷了3,就不能偷5;偷了5就不能偷3和2
输出:15
思路分析:可做如图1所示的过程分析,同种颜色虚线框为相同子问题。
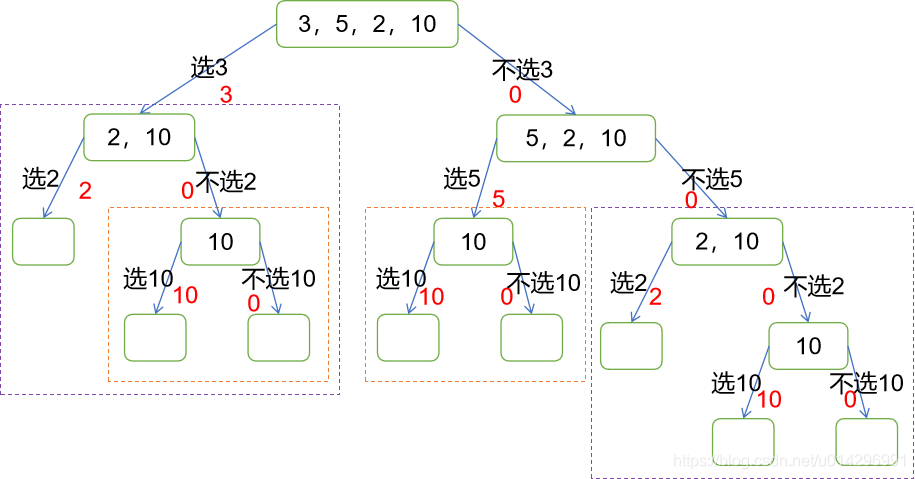
代码实现:
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
int GetMemo(int id, vector<int>& memo, vector<int>& houses)
{
if (id >= memo.size())
return 0;
if (memo[id] == -1) {
int selectFirstElement = houses[id] + GetMemo(id + 2,memo,houses);
int unselectFirstElement = GetMemo(id + 1, memo, houses);
memo[id] = max(selectFirstElement, unselectFirstElement);
}
return memo[id];
}
int GetGlod(vector<int>& houses)
{
vector<int> memo(houses.size(), -1); //memo是从第id房间到最后一房间能偷到的最大金子价值
return GetMemo(0, memo, houses);
}
int main()
{
vector<int> houses({ 3,5,2,10 });
cout << GetGlod(houses) << endl;
return 0;
}
扩展问题:如果是环怎么办,如果是树怎么办?
如果是环的话,只需要对第一个房间做出分析后便可转化为两个线性结构:(如图2)
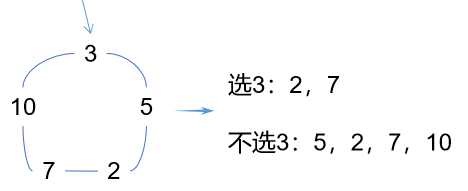
树和图结构同理。
总结:
备忘模型:
1.画解空间树(tree)
2.解空间树的节点表示(node)
3.重复节点(duplicate)
4.推理(infer)
5.自下到上进行演绎(若利用演绎模型做)
箴言录:
天下难事,必作于易;天下大事,必作于细。
 备忘录模型破解房屋盗窃难题
备忘录模型破解房屋盗窃难题





 本文通过一个具体的盗窃房屋问题,介绍了备忘录模型的使用方法,旨在解决不能连续盗窃的问题。文章详细解析了如何通过备忘录模型避免重复计算,提高效率,并给出了完整的代码实现。
本文通过一个具体的盗窃房屋问题,介绍了备忘录模型的使用方法,旨在解决不能连续盗窃的问题。文章详细解析了如何通过备忘录模型避免重复计算,提高效率,并给出了完整的代码实现。


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










