hdu 1086 计算几何 线段求交

原文链接

　　我们分两步确定两条线段是否相交：

　　(1)快速排斥试验

　　　　设以线段 P1P2 为对角线的矩形为R， 设以线段 Q1Q2 为对角线的矩形为T，如果R和T不相交，显然两线段不会相交。

　　(2)跨立试验

　　　　如果两线段相交，则两线段必然相互跨立对方。若P1P2跨立Q1Q2 ，则矢量 ( P1 - Q1 ) 和( P2 - Q1 )位于矢量( Q2 - Q1 ) 的两侧，即( P1 - Q1 ) × ( Q2 - Q1 ) * ( P2 - Q1 ) × ( Q2 - Q1 ) < 0。上式可改写成( P1 - Q1 ) × ( Q2 - Q1 ) * ( Q2 - Q1 ) × ( P2 - Q1 ) > 0。当 ( P1 - Q1 ) × ( Q2 - Q1 ) = 0 时，说明 ( P1 - Q1 ) 和 ( Q2 - Q1 )共线，但是因为已经通过快速排斥试验，所以 P1 一定在线段 Q1Q2上；同理，( Q2 - Q1 ) ×(P2 - Q1 ) = 0 说明 P2 一定在线段 Q1Q2上。所以判断P1P2跨立Q1Q2的依据是：( P1 - Q1 ) × ( Q2 - Q1 ) * ( Q2 - Q1 ) × ( P2 - Q1 ) >= 0。同理判断Q1Q2跨立P1P2的依据是：( Q1 - P1 ) × ( P2 - P1 ) * ( P2 - P1 ) × ( Q2 - P1 ) >= 0。具体情况如下图所示：

    

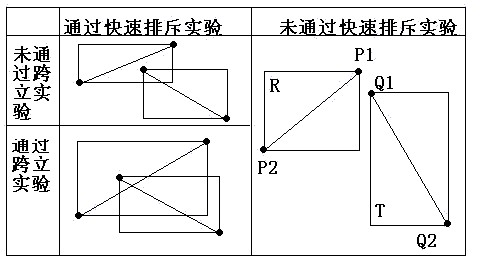
　　在相同的原理下，对此算法的具体的实现细节可能会与此有所不同，除了这种过程外，大家也可以参考《算法导论》上的实现。

关于计算几何算法概述网站 http://dev.gameres.com/Program/Abstract/Geometry.htm 一个挺好的网站

#include<stdio.h>
#include<iostream>
#include<math.h>
using namespace std;
#define EPS 1e-8


struct Point
{
    double x;
    double y;
};

struct Line
{
    Point f;  //first
    Point e;  //end
}l[105];

double Area2(Point p2, Point p3, Point p1)
{
    double temp = (p2.x - p1.x) * (p3.y - p1.y) - (p3.x - p1.x) * (p2.y - p1.y);
    return temp;
}

bool on_segment( Point p1,Point p2 ,Point p )
{
    double max1=p1.x > p2.x ? p1.x : p2.x ;
    double min1 =p1.x < p2.x ? p1.x : p2.x ;

    if( p.x >=min1 && p.x <=max1 )
        return true;
    else
        return false;
}

bool segInsert(Point p1, Point p2, Point p3, Point p4)
{
    double d1, d2, d3, d4;
    d1 = Area2(p1, p2, p3);
    d2 = Area2(p1, p2, p4);
    d3 = Area2(p3, p4, p1);
    d4 = Area2(p3, p4, p2);
    if ((d1 * d2 < -EPS) && (d3 * d4 < -EPS))
    {
       return true;
    }
    else if( fabs(d1) <= EPS && on_segment( p1,p2,p3 ) )
        return true;
    else if( fabs(d2) <= EPS&& on_segment( p1,p2,p4 ) )
        return true;
    else if( fabs(d3) <= EPS && on_segment( p3,p4,p1 ) )
        return true;
    else if( fabs(d4) <= EPS && on_segment( p3,p4,p2 ) )
        return true;
    return false;
}


int main()
{
  // freopen("E:\input.txt", "r", stdin);
    int n;
    int num;
    int i, j;
    while ((scanf("%d", &n)) && n != 0)
    {
        num = 0;
        for (i = 0; i < n; i++)
        {
            //scanf("%lf%lf%lf%lf",&l[i].f.x ,&l[i].f.y ,&l[i].e.x ,&l[i].e.y );
            cin >> l[i].f.x >> l[i].f.y >> l[i].e.x >> l[i].e.y;
        }
        for (i = 0; i < n; i++)
        {
            for (j = i + 1; j < n; j++)
            {
                if (segInsert(l[i].f, l[i].e, l[j].f, l[j].e))
                {
                    num++;
                }
            }
        }
        cout << num << endl;
    }

    return 0;
}

参考博客

搜索

复制