NYOJ 148 fibonacci数列(二)

最新推荐文章于 2017-09-13 19:03:06 发布

Or_me

最新推荐文章于 2017-09-13 19:03:06 发布

阅读量854

点赞数

CC 4.0 BY-SA版权

分类专栏：数学 ojs 文章标签：数学矩阵计算

本文链接：https://blog.youkuaiyun.com/tcm_zhangpeng/article/details/20573763

ojs 同时被 2 个专栏收录

20 篇文章

订阅专栏

数学

19 篇文章

订阅专栏

本文介绍了一种高效计算Fibonacci数列第n项末尾四位数的方法，通过矩阵快速幂算法优化计算过程，适用于大规模n值的情况。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

fibonacci数列(二)

时间限制：1000 ms | 内存限制：65535 KB

难度：3

描述

In the Fibonacci integer sequence, F₀ = 0, F₁ = 1, andF_n =F_n_{− 1} +F_n_{− 2} forn ≥ 2. For example, the first ten terms of the Fibonacci sequence are:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …

An alternative formula for the Fibonacci sequence is

Given an integer n, your goal is to compute the last 4 digits of F_n.

Hint

As a reminder, matrix multiplication is associative, and the product of two 2 × 2 matrices is given by

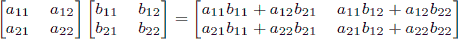Also, note that raising any 2 × 2 matrix to the 0th power gives the identity matrix:

输入

The input test file will contain multiple test cases. Each test case consists of a single line containing n (where 0 ≤ n ≤ 1,000,000,000). The end-of-file is denoted by a single line containing the number −1.

输出

For each test case, print the last four digits of Fn. If the last four digits of Fn are all zeros, print ‘0’; otherwise, omit any leading zeros (i.e., print Fn mod 10000).

样例输入

样例输出

0
34
6875

矩阵快速幂...好高级

 如:求A^156,而156(10)=10011100(2) 也就有A^156=>(A^4)*(A^8)*(A^16)*(A^128) 考虑到因子间的联系，我们从二进制10011100中的最右端开始计算到最左端。细节就说到这，下面给核心代码：

while(N)
 {
                if(N&1)
                       res=res*A;
                N>>=1;
                A=A*A;
 }

贴个本题的最优：

#include <stdio.h>
int f(int x,int y,int a,int b)
{
    return a*x+b*y;
}
int main()
{
    int n,i,j,k;
    while(scanf("%d",&n)&&~n)
    { 
        int t[2][2];
        int a[2][2]=
        {
            1,0,
            1,0
        };
        int b[2][2]=
        {
            1,1,
            1,0
        };
       
        while(n)
        {
            if(n&1)
            {
                t[0][0]=f(a[0][0],a[0][1],b[0][0],b[1][0])%10000;
                t[0][1]=f(a[0][0],a[0][1],b[0][1],b[1][1])%10000;
                t[1][0]=f(a[1][0],a[1][1],b[0][0],b[1][0])%10000;
                t[1][1]=(a[1][0],a[1][1],b[0][1],b[1][1])%10000;
                a[0][0]=t[0][0];
                a[0][1]=t[0][1];
                a[1][0]=t[1][0];
                a[1][1]=t[1][1];
            }
            t[0][0]=f(b[0][0],b[0][1],b[0][0],b[1][0])%10000;
            t[0][1]=f(b[0][0],b[0][1],b[0][1],b[1][1])%10000;
            t[1][0]=f(b[1][0],b[1][1],b[0][0],b[1][0])%10000;
            t[1][1]=f(b[1][0],b[1][1],b[0][1],b[1][1])%10000;
            b[0][0]=t[0][0];
            b[0][1]=t[0][1];
            b[1][0]=t[1][0];
            b[1][1]=t[1][1];
            n=n>>1;
        }
        printf("%d\n",a[0][1]);
    }
    return 0;
}