2018年湘潭大学程序设计竞赛 G 又见斐波那契【矩阵快速幂】

本文介绍了一个增强版的斐波那契数列问题，通过构建转移矩阵使用矩阵快速幂方法解决大规模数值计算的问题，并提供了一段C语言实现的代码示例。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

时间限制：C/C++ 1秒，其他语言2秒
空间限制：C/C++ 32768K，其他语言65536K
64bit IO Format: %lld

题目描述

这是一个加强版的斐波那契数列。

给定递推式

求F(n)的值，由于这个值可能太大，请对109+7取模。

输入描述:

第一行是一个整数T(1 ≤ T ≤ 1000)，表示样例的个数。
以后每个样例一行，是一个整数n(1 ≤ n ≤ 1018)。

输出描述:

每个样例输出一行，一个整数，表示F(n) mod 1000000007。

示例1

输入

输出

思路：

(i+1)^3=i^3+3*i^2+3*i+1;

(i+1)^2=i^2+2*i+1;

i+1=i+1;

根据以上方程构造转移矩阵：

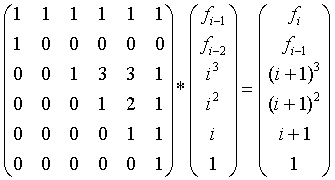
代码：

#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;
#define mod 1000000007
typedef long long LL;
struct state
{
    LL a[6][6];
};
state multi(state a,state b)
{
    state c={0};
    for(int i=0;i<6;i++)
    for(int j=0;j<6;j++)
    for(int k=0;k<6;k++)
    c.a[i][j]=(c.a[i][j]+a.a[i][k]*b.a[k][j])%mod;
    return c;
}
state quick_pow(state a,LL n)
{
    state b={0};
    for(int i=0;i<6;i++)
        b.a[i][i]=1;
    while(n)
    {
        if(n&1) b=multi(a,b);
        a=multi(a,a);
        n>>=1;
    }
    return b;
}
int main()
{
    int t;
    scanf("%d",&t);
    LL n;
    while(t--)
    {
        scanf("%lld",&n);
        state a={0},b={0};
        for(int i=0;i<6;i++)
            a.a[0][i]=1;
        a.a[1][0]=1;
        a.a[2][2]=a.a[2][5]=1;
        a.a[2][3]=a.a[2][4]=3;
        a.a[3][3]=a.a[3][5]=1;
        a.a[3][4]=2;
        a.a[4][4]=a.a[4][5]=1;
        a.a[5][5]=1;
        b.a[0][0]=1;
        b.a[1][0]=0;
        b.a[2][0]=8;
        b.a[3][0]=4;
        b.a[4][0]=2;
        b.a[5][0]=1;
        printf("%lld\n",multi(quick_pow(a,n),b).a[1][0]);
    }
    return 0;
}