注:本文为 “Lloyd-Max” 相关合辑。
略作重排,如有内容异常,请看原文。
Lloyd-Max 迭代
posted @ 2015-06-22 22:31 Loyal_1884



数据压缩补充知识——量化器(Lloyd-Max 条件推导)
Adore11 已于 2022-07-13 00:34:56 修改
一、基础知识
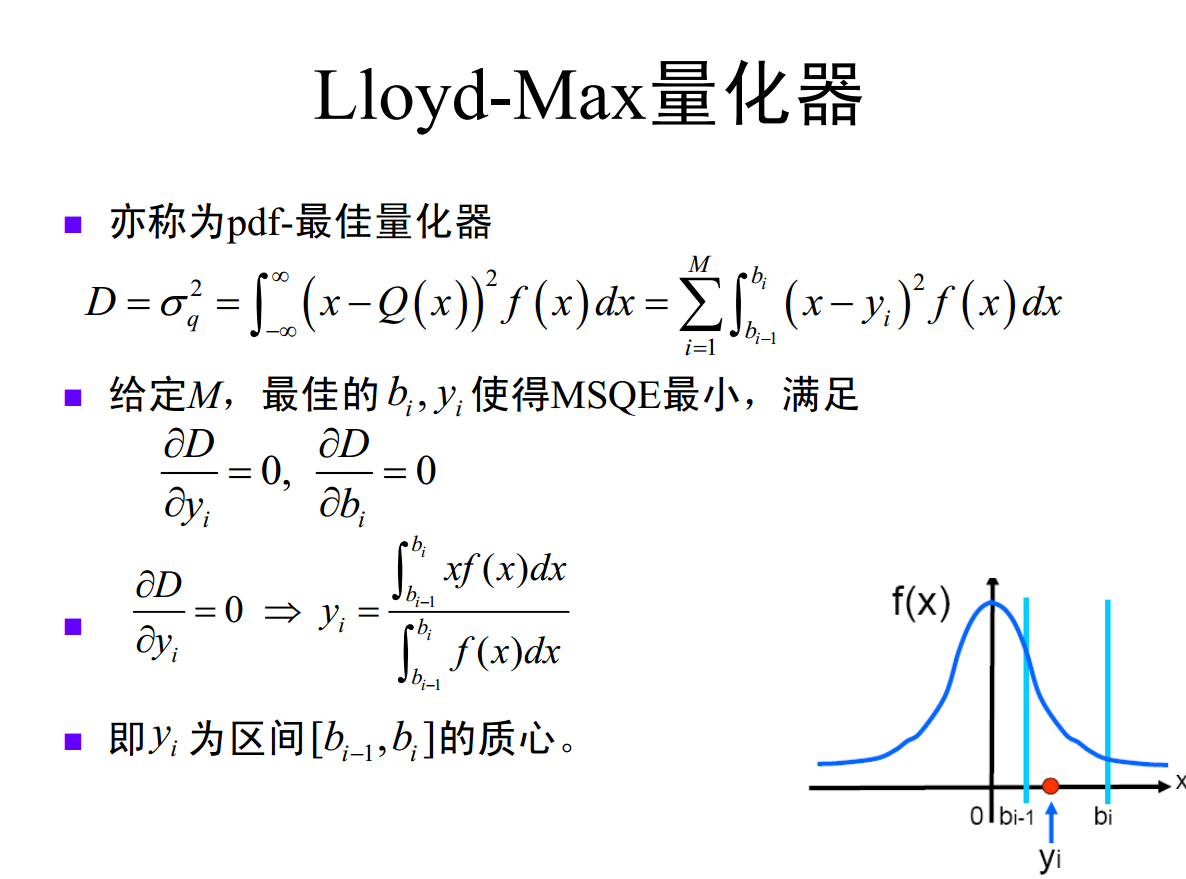
Lloyd-Max 标量量化器(非均匀量化器):又称概率密度函数(Probability Density Function, PDF)最优量化器。

量化设计需考虑的核心要点如下:

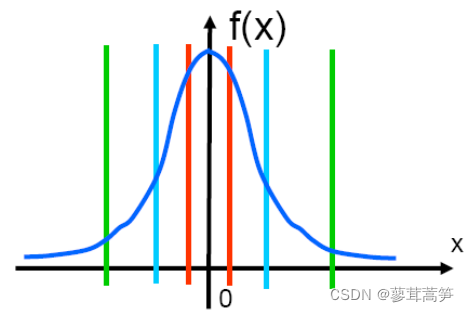
Lloyd-Max 量化器的核心设计准则为:在信源符号概率密度函数 ( f_X(x) ) 取值较大的区域,减小量化区间宽度;在 ( f_X(x) ) 取值较小的区域,增大量化区间宽度。其本质是对出现概率高的信源符号采用“细量化”(小区间),对出现概率低的信源符号采用“粗量化”(大区间),以实现量化失真的最小化。
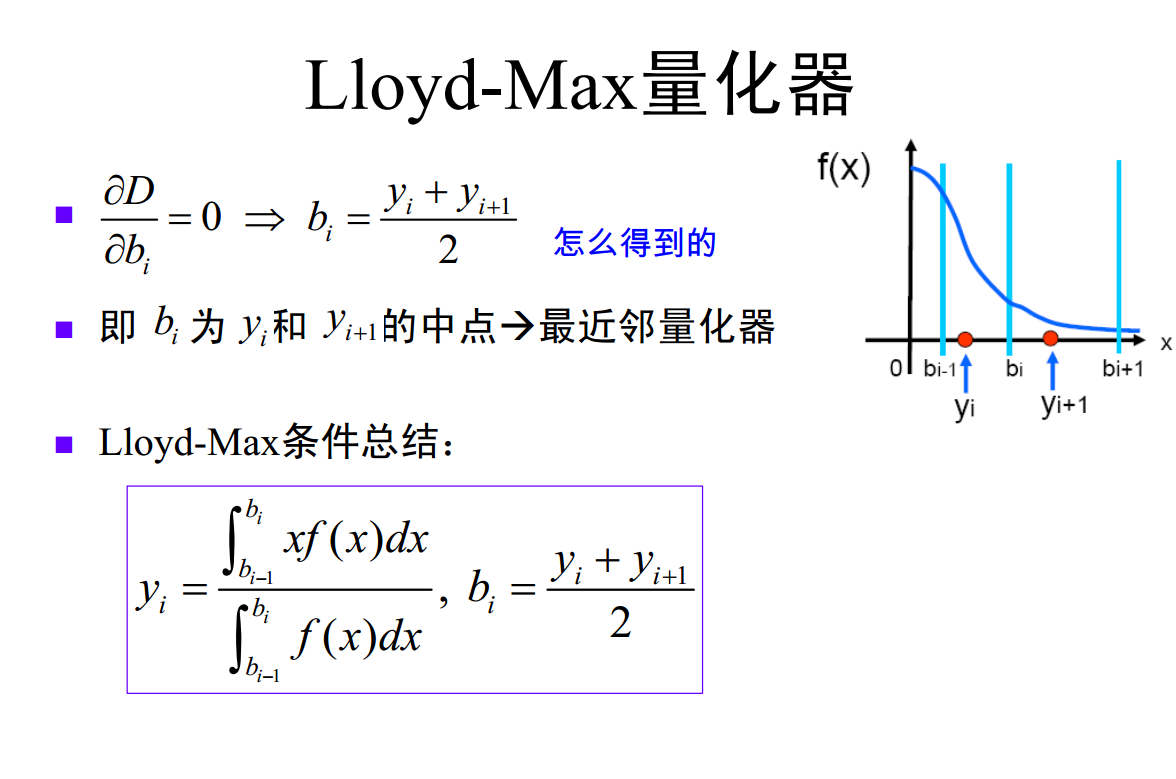
基于上述准则,可引出 Lloyd-Max 量化器的两个核心结论:

- 量化判决门限应取于相邻两个量化重建电平的中点;
- 量化重建电平应取于对应量化区间的质心。
下文将对上述两个核心结论进行数学推导。
二、条件推导
为清晰呈现推导过程与逻辑关系,采用手写推导形式,具体如下:

三、重要结论
- 对于服从均匀分布的信源信号,采用均匀量化器可实现最优量化性能(即最小化量化失真)。
- 对于服从非均匀分布的信源信号,采用 Lloyd-Max 量化器可实现最优量化性能;当输入信号退化为均匀分布时,Lloyd-Max 量化器与均匀量化器的性能完全一致(即 Lloyd-Max 量化器是均匀量化器的广义推广)。
尽管 Lloyd-Max 量化器可针对非均匀分布信号实现最小量化失真(其“概率高区域细量化、概率低区域粗量化”的特性,使量化失真显著优于均匀量化),但在实际数据压缩系统中,还需结合后续熵编码环节的需求综合考量——量化后的输出需输入熵编码器(如 Huffman 编码器、算术编码器等),最终生成压缩码流。
熵编码的核心优化目标是“最小化平均码长”,其实现依赖于输入符号的概率分布特性:对于概率分布非均匀的输入符号集,熵编码器可对高概率符号分配短码长、对低概率符号分配长码长,从而显著降低平均码长,提升压缩效率;反之,若输入符号概率分布均匀,则熵编码难以实现有效压缩。
为进一步验证上述特性,回顾非均匀量化与均匀量化的输出概率分布差异:
1. 非均匀量化输出的概率分布
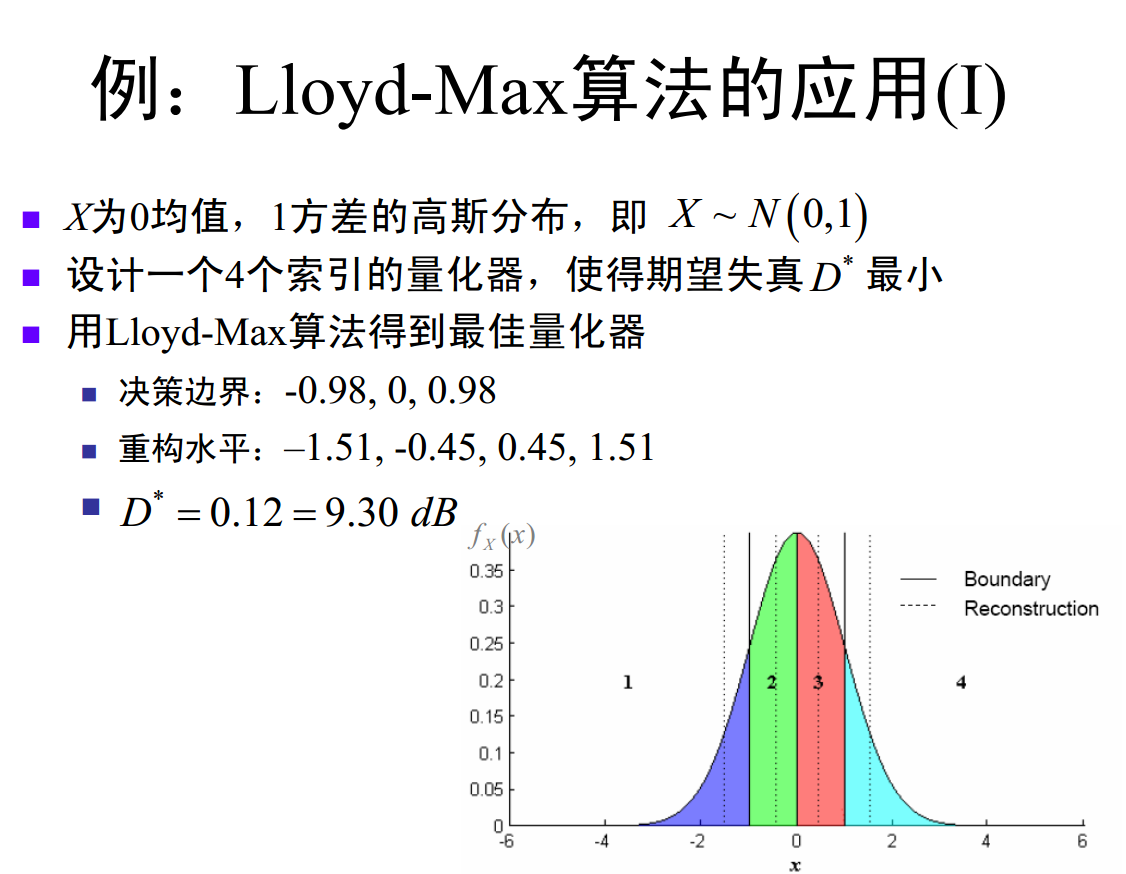
非均匀量化(以 Lloyd-Max 量化器为例)的输出符号概率分布如图所示:

图中编号为 1、2、3、4 的量化区间,其对应输出符号的出现概率(可通过各区间的面积近似表征,即概率密度函数在区间内的积分)近乎相等,即输出符号服从均匀分布。
2. 均匀量化输出的概率分布
均匀量化的输出符号概率分布如图所示:

图中编号为 3、4、5、6、7、8 的量化区间,其对应输出符号的出现概率存在显著差异(高概率密度区域的区间对应高输出概率,低概率密度区域的区间对应低输出概率),即输出符号服从非均匀分布。
最终结论
综合量化失真与熵编码效率的权衡,可得到如下核心结论:
- 非均匀量化:输出符号服从均匀分布 → 熵编码难以实现有效压缩(不适合熵编码);
- 均匀量化:输出符号服从非均匀分布 → 熵编码可通过“长短码分配”降低平均码长(适合熵编码)。
因此,在实际数据压缩系统中,直接采用均匀量化器是兼顾量化失真与压缩效率的优选方案。
【数据压缩】Lloyd-Max 标量量化器
蓼茸蒿笋 已于 2022-04-21 19:09:13 修改
一、问题引入
-
均匀量化器仅对均匀分布信源具有最优性(即最小化均方误差)。其中,均匀分布信源的概率密度函数(Probability Density Function, PDF)满足 f ( x ) = 1 b − a f(x) = \frac{1}{b-a} f(x)=b−a1( x ∈ [ a , b ] x \in [a,b] x∈[a,b], a a a、 b b b 分别为信源取值的上下界),此时均匀量化的区间划分可使均方误差最小;若信源非均匀分布,均匀量化器的性能会显著下降。
-
对于给定的量化级数 M M M,为降低均方误差(Mean Square Error, MSE),需依据信源 PDF 调整量化区间:在信源概率密度 f ( x ) f(x) f(x) 较大的区域缩小量化区间(提高量化精度),在 f ( x ) f(x) f(x) 较小的区域增大量化区间(降低冗余)。
二、推导过程

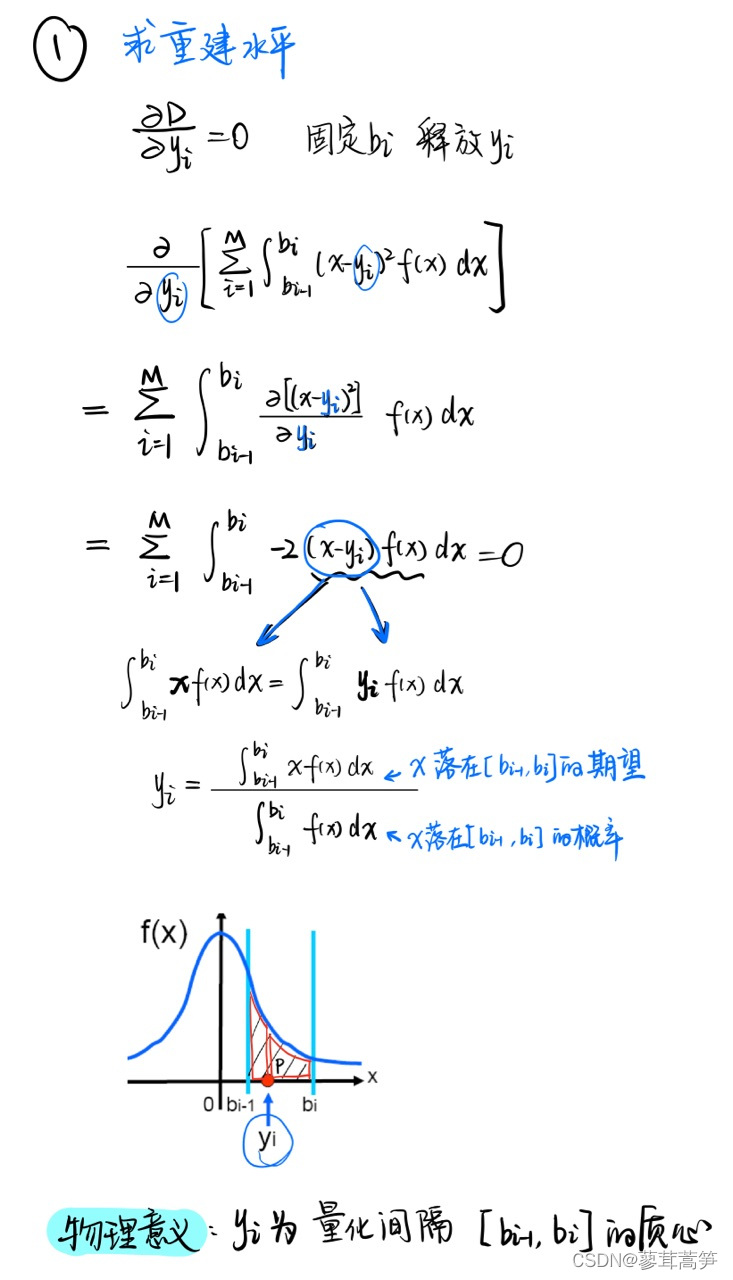

三、推导结论
- 结论 1(重建电平优化):量化电平(即重建电平) x ^ i \hat{x}_i x^i 应取为对应量化区间的质心,确保该区间内的失真积分最小。
- 结论 2(决策边界优化):判决电平(即量化区间边界) t i t_i ti 应取为相邻两个重建电平的中点,使边界两侧的失真贡献均衡。
via:
-
Lloyd-Max 迭代 - Loyal_1884 - 博客园
https://www.cnblogs.com/pphy1884/p/4594084.html -
数据压缩补充知识——量化器(Lloyd-Max 条件推导)-优快云博客
https://blog.youkuaiyun.com/Adore11/article/details/125754454 -
【数据压缩6】LIoyd-Max 标量量化器_均匀量化重建电平-优快云博客
https://blog.youkuaiyun.com/m0_46357931/article/details/124322904 -
lloyd-max 最优标量量化算法分析 - feiyangyy94 - 博客园
https://www.cnblogs.com/fyyy94/p/18131497





















 1232
1232

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








