光 | 普洛克斯坦床效应

注：机翻，未校。

---

The Procrustean Bed effect for light

光的普罗克鲁斯特斯床效应

Adolfo Santa Fe Dueñas
阿道夫·圣达菲·杜埃尼亚斯

Department of Physics and Astronomy, University of Texas at San Antonio, San Antonio, TX 78249, USA
Space Science and Engineering Division, Southwest Research Institute, San Antonio, TX 78228, USA
Received 14 July 2023, Revised 24 October 2023, Accepted 10 November 2023, Available online 14 November 2023, Version of Record 16 November 2023.

Abstract

摘要

This paper proposes a new way of describing the propagation of light between an emitter and an observer in relative motion as an alternative to Lorentz transformations and the relativistic Doppler effect. We introduce a refined Doppler effect that we call the Procrustean Bed (PB) effect for light, where light waves change in frequency, length, and speed. The PB confirms the wave nature of light and acknowledges the existence of a luminiferous medium (ether) that conditions a constant speed of light in accordance with Maxwell’s predictions. Our results are consistent with the Ives-Stilwell experiment (a fundamental test to validate special relativity), relating the transmitted light frequency to the geometric mean of its observed parallel and anti-parallel frequencies. However, PB revealed that emitters and observers can have relative motions beyond the speed of light, where negative frequencies can be observed, which in some cases appear to come from the opposite direction of their source. If this effect is applied to gravity waves, it may result in observers experiencing a repulsive gravity, which may contribute to the expanding universe.
本文提出了一种描述相对运动中发射体与观察者之间光传播的新方法，以替代洛伦兹变换和相对论多普勒效应。我们引入了一种改进的多普勒效应，称之为光的普罗克鲁斯特斯床（PB）效应，其中光波的频率、波长和速度会发生变化。PB 效应证实了光的波动性质，并承认存在光以太介质（ether），该介质使光速保持恒定，符合麦克斯韦的预测。我们的结果与艾夫斯-斯蒂尔韦尔实验（验证狭义相对论的基础测试）一致，该实验将发射光频率与观测到的平行和反平行频率的几何平均值相关联。然而，PB 效应表明，发射体和观察者可以有超过光速的相对运动，此时可能观测到负频率，在某些情况下，这些负频率似乎来自其源的相反方向。如果将这一效应应用于引力波，可能会导致观察者体验到排斥性引力，这可能有助于解释宇宙的膨胀。

Keywords

关键词

Relativity; Doppler effect; supraluminal; Gravitational waves; Antigravity; Expanding universe
相对论；多普勒效应；超光速；引力波；反重力；膨胀的宇宙

Introduction

引言

Maxwell’s equations, published in his “On physical lines of force” paper [1], are a compilation of partial differential equations describing magnetism and electricity. These equations were originally a set of about 20 equations developed and integrated by different authors [2]. The integration resulted in four equations, now known as Maxwell’s equations, which are shown in Table 1, where E is the electric field, B is the magnetic field, J is the electric current density, ε₀ and μ₀ are the permittivity and the permeability of free space, respectively.
麦克斯韦方程组发表在他的《论物理力线》论文 [1] 中，是描述磁和电的偏微分方程组的汇编。这些方程最初是由不同作者开发和整合的约 20 个方程的集合 [2]。整合后得到四个方程，现在称为麦克斯韦方程组，如表 1 所示，其中 E 是电场，B 是磁场，J 是电流密度，ε₀ 和 μ₀ 分别是自由空间的介电常数和磁导率。

Table 1. Maxwell’s equations.
表 1. 麦克斯韦方程组（微分形式）

Name	Equation
Gauss’s Law 高斯定律	$\vec{\nabla }\cdot \vec{E}=\frac{\rho }{{ϵ}_0}$
Gauss’s Law for magnetism 磁学高斯定律	$\vec{\nabla }\cdot \vec{B}=0$
Faraday’s Law of induction 法拉第电磁感应定律	$\vec{\nabla }\times \vec{E}=-\frac{\partial \vec{B}}{\partial t}$
Ampere’s Law 安培定律	$\vec{\nabla }\times \vec{B}={\mu }_0\vec{J}+{ϵ}_0{\mu }_0\frac{\partial \vec{E}}{\partial t}$

安培定律中的“麦克斯韦修正项”（即位移电流项 ${\mu }_0{\epsilon }_0\frac{\partial \mathbf{E}}{\partial t}$），使方程组在电磁学中具备完整性，是描述电磁场演化的核心部分。

By using these equations, Maxwell was able to predict the existence of electromagnetic waves that propagate at a constant speed ( $\frac{1}{\sqrt{{\epsilon }_0{\mu }_0}}$). Maxwell realized that this speed in these electromagnetic waves was very similar to experimental measurements of the speed of light calculated by Weber and Kohlrausch [3], Fizeau [4] and Foucault [5], and concluded that light should also be an electromagnetic wave [6].
通过使用这些方程，麦克斯韦能够预测以恒定速度（ $\frac{1}{\sqrt{{\epsilon }_0{\mu }_0}}$）传播的电磁波的存在。麦克斯韦意识到，这些电磁波的速度与韦伯和科尔劳施 [3]、菲佐 [4] 和傅科 [5] 计算的光速实验测量值非常相似，并得出结论：光也应该是一种电磁波 [6]。

Einstein took these findings to formulate the second postulate of his special theory of relativity (the constancy of the speed of light) [7]. Einstein also adopted ideas of Poincaré [8] and Lorentz [9] to present what became known as the special theory of relativity or special relativity (SR).
爱因斯坦利用这些发现提出了狭义相对论的第二个假设（光速不变）[7]。爱因斯坦还采用了庞加莱 [8] 和洛伦兹 [9] 的思想，提出了后来被称为狭义相对论或特殊相对论（SR）的理论。

Lorentz transformations

洛伦兹变换

Hendrik Lorentz derived his Lorentz transformations (LT) prior to the proposal of SR. However, there are many methods for deriving the LT based on the postulates of SR. One of them is as follows:
亨德里克·洛伦兹在狭义相对论提出之前就推导出了他的洛伦兹变换（LT）。然而，基于狭义相对论的假设，有许多推导洛伦兹变换的方法。其中一种方法如下：

Have two inertial frames O and O’, identical at t = t’ = 0 when the axes and origin coincide, and the inertial frames be in relative motion with constant speed v. This configuration is known as the standard configuration and is shown in Fig. 1.
有两个惯性系 O 和 O’，在 t = t’ = 0 时轴和原点重合，惯性系以恒定速度 v 相对运动。这种配置称为标准配置，如图 1 所示。

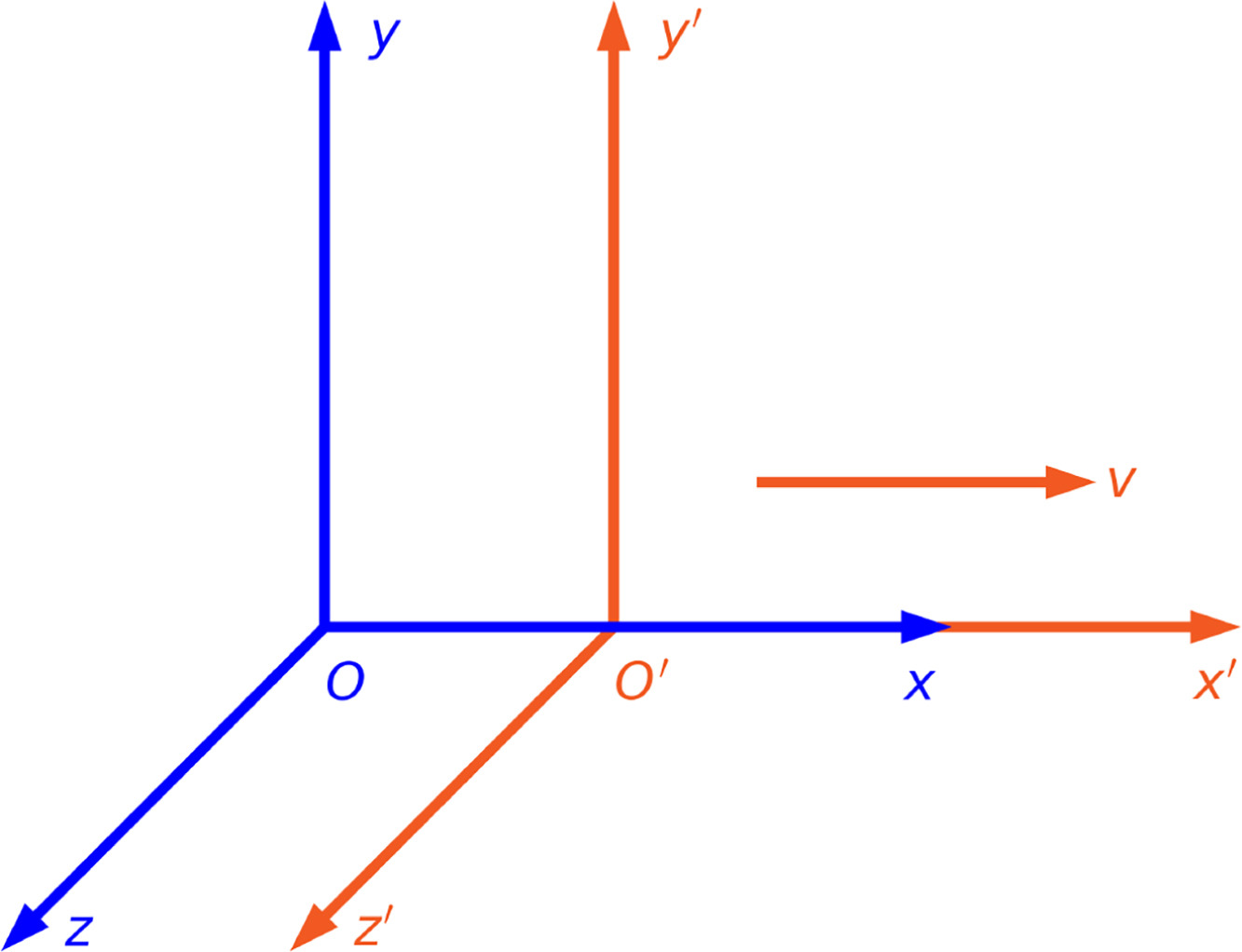
Figure 1. The standard configuration used in special relativity. The primed (orange) system is moving at a speed $u$ along the $x$-axis relative to the unprimed (blue) system.
图 1. 特殊相对论中使用的标准配置。橙色（带撇号）系统沿 $x$ 轴以速度 $u$ 相对于蓝色（无撇号）系统运动。

According to SR, the speed of light is the same in both frames, regardless of their relative motion, therefore, if a light signal is emitted in all directions at t = t’ = 0 from the common origin, the light wavefront will have the same spherical shape in both frames (shown as yellow circles in Fig. 2).
根据狭义相对论，无论相对运动如何，光速在两个参考系中都是相同的，因此，如果在 t = t’ = 0 时从共同原点向所有方向发射光信号，光波前在两个参考系中都将具有相同的球形（如图 2 中的黄色圆圈所示）。

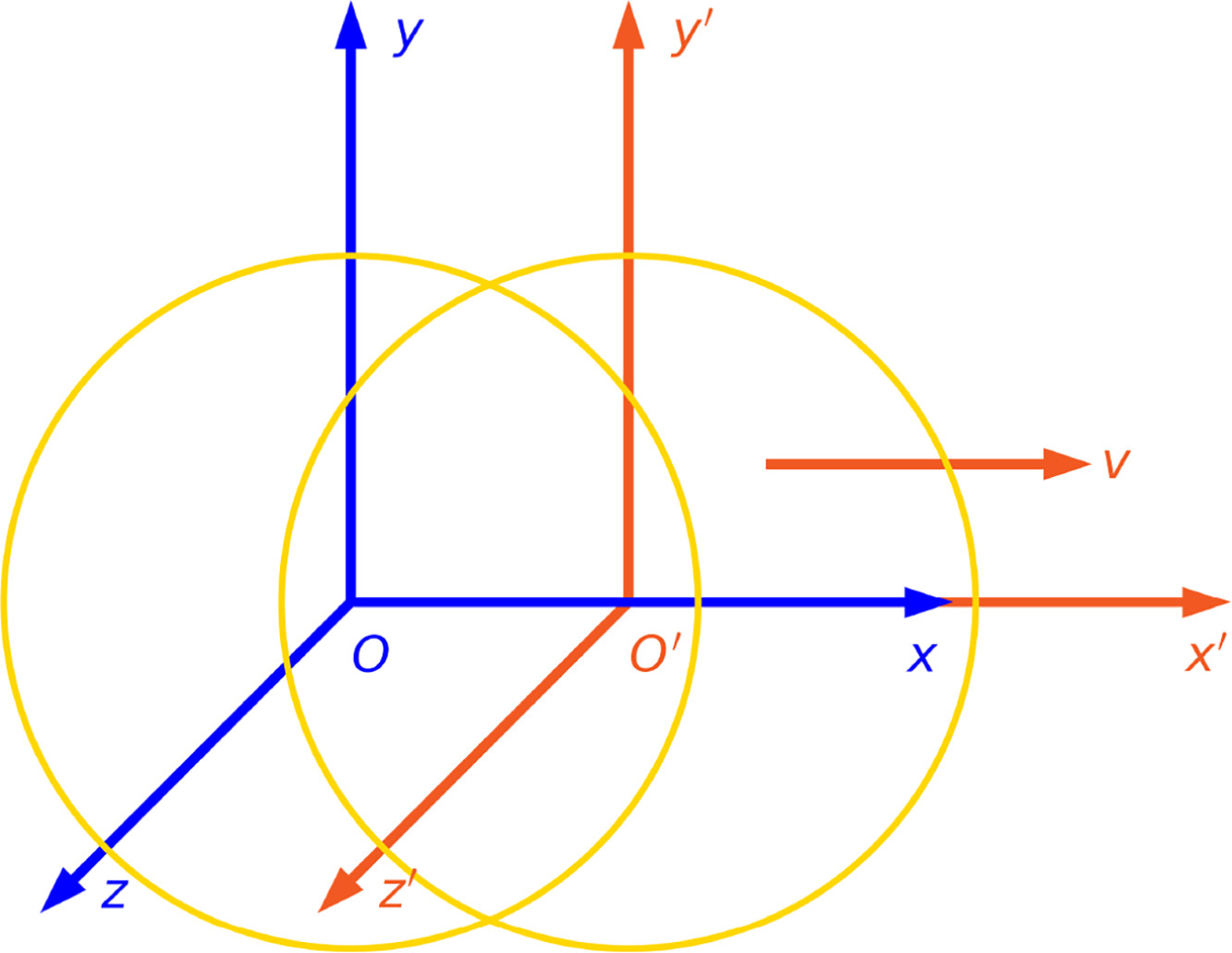
Figure 2. Spherical wavefronts (yellow circles) produced by the same light event in two different frames in relative motion, according to special relativity.
图 2.根据特殊相对论，两个相对运动的不同参考系中由同一光事件产生的球形波前（黄色圆圈）。

This means that, for SR, the original light event is able to produce a spherical waveform expanding at the speed of light c in both frames and centered at both frame origins even when the origins are separated by a distance vt. Although this is counterintuitive, it is mathematically postulated and expressed by the set of equations which are known as the Lorentz transformations (LT):
这意味着，对于狭义相对论，即使原点相距 vt 的距离，原始光事件也能够在两个参考系中产生以光速 c 扩展并以两个参考系原点为中心的球形波形。尽管这有违直觉，但它在数学上被假设并由一组称为洛伦兹变换（LT）的方程表示：

$$\begin{array}{rl}{x}^{\prime }& =\gamma (x-vt)\\ y^{\prime }& =y\\ z^{\prime }& =z\\ t^{\prime }& =\gamma \left(t-\frac{vx}{c^2}\right)\end{array}\text{\hspace{1em}(1)(2)(3)(4)}$$

where $\gamma =\frac{1}{\sqrt{1-{\beta }^2}}$ is known as the Lorentz factor and $\beta =\frac{v}{c}$ [10].

其中$\gamma =\frac{1}{\sqrt{1-{\beta }^2}}$ 是洛伦兹因子，$\beta =v/c$ [10]。

In the LT, both space and time undergo a Procrustean process where they are stretched or contracted to fit in the equations in favor of a constant speed of light. By this effect, however, space and time lose their absoluteness. As a result, the SR theory leads to many paradoxes, such as the Twin and Grandfather paradoxes [11, 12, 13]. When v is very small compared to c, or when c tends to infinite, these equations become the Galilean transformations:
在洛伦兹变换中，空间和时间都经历了一个普罗克鲁斯特斯过程，它们被拉伸或收缩以适应方程，以支持恒定的光速。然而，由于这种效应，空间和时间失去了它们的绝对性。结果，狭义相对论理论导致了许多悖论，如双生子悖论和祖父悖论 [11, 12, 13]。当 v 与 c 相比非常小时，或者当 c 趋于无穷大时，这些方程就变成了伽利略变换：

$$\begin{array}{rl}{x}^{\prime }& =x-vt\\ y^{\prime }& =y\\ z^{\prime }& =z\\ t^{\prime }& =t\end{array}\text{\hspace{1em}(5)(6)(7)(8)}$$

Relativistic Doppler effect

相对论多普勒效应

The observed change in the period and frequency rates of a clock due to its relative motion with respect to an observer cannot be estimated using Eq. (4) directly, as originally proposed by Einstein [14]; instead, in SR, the change in length and frequency of a light wave due to the relative motion between the source of light and the observer is given by the relativistic Doppler effect (RDE), where the classical Doppler effect (CDE) from the point of view of the observer $f_{obs}=f_{src}/(1+\beta )$, is time dilated by the Lorentz factor γ.
由于时钟相对于观察者的相对运动而观察到的周期和频率变化不能像爱因斯坦最初提出的那样直接使用方程（4）来估计 [14]；相反，在狭义相对论中，由于光源和观察者之间的相对运动而引起的光波波长和频率的变化由相对论多普勒效应（RDE）给出，其中从观察者的角度来看，经典多普勒效应（CDE）$f_{obs}=f_{src}/(1+\beta )$ 被洛伦兹因子 γ 时间膨胀。

$$f_{obs}=(1/\gamma )f_{src}/(1+\beta )=\surd (1-{\beta }^2)/(1+\beta )f_{src}=\surd ((1-\beta )/(1+\beta ))f_{src}\text{\hspace{1em}(9)}$$

If, instead, we use the CDE from the point of view of the source $f_{obs}=f_{src}(1-\beta )$, we would need to multiply by γ to obtain the same expression.
如果相反，我们使用从源的角度来看的经典多普勒效应 $f_{obs}=f_{src}(1-\beta )$，我们需要乘以 γ 以获得相同的表达式。

$$f_{obs}=\gamma (1-\beta )f_{src}=(1-\beta )/\surd (1-{\beta }^2)f_{src}=\surd ((1-\beta )/(1+\beta ))f_{src}\text{\hspace{1em}(10)}$$

The observed wavelength is given by
观察到的波长由下式给出
$${\lambda }_{obs}=\surd ((1+\beta )/(1-\beta )){\lambda }_{src}\text{\hspace{1em}(11)}$$

These relations were used in the Ives-Stilwell experiment [15] where the authors compared the observed parallel (red-shifted) and anti-parallel (blue-shifted) wavelength shifts of hydrogen clocks traveling at 0.005c to the expected values of the CDE (${\lambda }_p=(1-\beta ){\lambda }_{src}$ and ${\lambda }_a=(1+\beta ){\lambda }_{src}$) and the RDE (${\lambda }_p=\surd ((1-\beta )/(1+\beta )){\lambda }_{src}$ and ${\lambda }_a=\surd ((1+\beta )/(1-\beta )){\lambda }_{src}$). The results showed agreement with the RDE: therefore, the authors concluded that the RDE theory was verified. The Ives-Stilwell experiment is considered one of the fundamental tests of SR [16].
这些关系在艾夫斯-斯蒂尔韦尔实验 [15] 中得到了应用，作者将以 0.005c 速度行进的氢钟的观察到的平行（红移）和反平行（蓝移）波长偏移与经典多普勒效应（CDE）（${\lambda }_p=(1-\beta ){\lambda }_{src}$ 和 ${\lambda }_a=(1+\beta ){\lambda }_{src}$）和相对论多普勒效应（RDE）（${\lambda }_p=\surd ((1-\beta )/(1+\beta )){\lambda }_{src}$ 和 ${\lambda }_a=\surd ((1+\beta )/(1-\beta )){\lambda }_{src}$）的预期值进行了比较。结果表明与相对论多普勒效应一致：因此，作者得出结论，相对论多普勒效应理论得到了验证。艾夫斯-斯蒂尔韦尔实验被认为是狭义相对论的基础测试之一 [16]。

One of the difficulties with the Ives-Stilwell experiment is the uncertainty of β, i.e. the ratio of the velocity of the hydrogen clocks to c. To get rid of uncertainties of β, modern Ives-Stilwell experiments [17, 18, 19] compute the source frequency (f_src) by multiplying the observed parallel (red-shifted) and anti-parallel frequencies ($f_p$ and $f_a$) as follows:
艾夫斯-斯蒂尔韦尔实验的困难之一是 β 的不确定性，即氢钟速度与 c 的比率。为了消除 β 的不确定性，现代艾夫斯-斯蒂尔韦尔实验 [17, 18, 19] 通过将观察到的平行（红移）和反平行频率（f_p 和 f_a）相乘来计算源频率（f_src），如下所示：

Given that $f_p=\surd ((1-\beta )/(1+\beta ))f_{src}$ and $f_a=\surd ((1+\beta )/(1-\beta ))f_{src}$
$$f_p{f}_a=\surd ((1+\beta )/(1-\beta ))f_{src}\surd ((1-\beta )/(1+\beta ))f_{src}\text{\hspace{1em}(12)}$$
$$f_p{f}_a=f_{src}^2\text{\hspace{1em}(13)}$$
Or
$$\surd (f_p{f}_a)=f_{src}\text{\hspace{1em}(14)}$$
即，无论 v 的值如何，f_src 都可以通过 f_p 和 f_a 的几何平均值来估计。随着现代实验的出现，这种测量的精度得到了提高，例如，Botermann 等人 [19] 实现了 <4×10⁻⁹ 的精度。

One limitation of the RDE, inherited from the Lorentz factor, γ, is that v cannot exceed the value of c, given that the square root of a negative number does not have a definite value.
相对论多普勒效应（RDE）的一个局限性，继承自洛伦兹因子 γ，是 v 不能超过 c 的值，因为负数的平方根没有确定的值。

Thus, for SR, and in turn for the RDE, the ultimate velocity for all moving objects including light is c. However, a number of studies have reported apparent supraluminal velocities in extragalactic radio sources [20] and receding galaxies that question the current interpretation of the universe expansion [21].
因此，对于狭义相对论，进而对于相对论多普勒效应，包括光在内的所有运动物体的最终速度是 c。然而，许多研究报告了河外射电源 [20] 和退行星系中明显的超光速速度，这对当前对宇宙膨胀的解释提出了质疑 [21]。

In this study, we propose still developing alternatives to the LT and the RDE that seem to agree with the Ives-Stilwell experiments but allow faster-than-light relative motions.
在这项研究中，我们提出了仍在发展的洛伦兹变换和相对论多普勒效应的替代方案，这些方案似乎与艾夫斯-斯蒂尔韦尔实验一致，但允许超光速的相对运动。

Methodology

方法

As in Newtonian relativity, we assume the existence of an absolute space, in which inertial frames are in uniform motion and share a universal time. In this space, all objects have their own space coordinates and share an absolute time. In general, observers perceive the space-time coordinates of objects through light. For speeds and distances relatively small (compared to c), light is, in general, considered to travel instantly. However, light has a limited speed; therefore, the information observed through light is always delayed. We use (x, t) to indicate the actual space-time coordinates of objects and (x’, t’) for the observed space-time coordinates emitted through light by the observed objects.
与牛顿相对论一样，我们假设存在绝对空间，其中惯性系做匀速运动并共享通用时间。在这个空间中，所有物体都有自己的空间坐标并共享绝对时间。一般来说，观察者通过光感知物体的时空坐标。对于相对较小的速度和距离（与 c 相比），通常认为光瞬间传播。然而，光的速度是有限的；因此，通过光观察到的信息总是延迟的。我们使用 (x, t) 表示物体的实际时空坐标，使用 (x’, t’) 表示被观察物体通过光发射的观察到的时空坐标。

Light is believed to propagate either as a corpuscular phenomenon (as seen by Newton) or as a wave phenomenon (as seen by Huygens) [22]. If light propagates as a corpuscular phenomenon, no medium of propagation is needed, and the observed speed of light will depend on the relative motion between its source and its observer. However, light propagating as a wave requires a medium, like air or water for sound.
光被认为要么以粒子现象传播（如牛顿所见），要么以波动现象传播（如惠更斯所见）[22]。如果光以粒子现象传播，则不需要传播介质，观察到的光速将取决于其源和观察者之间的相对运动。然而，作为波传播的光需要介质，就像声音需要空气或水一样。

In our approach, two observers (A and B) depart at the same speed (v/2) in opposite directions from a witness (W) at time t = 0, where v is the speed at which A and B separate from each other. In this configuration, the delayed time of B (t_B’) observed by A at time t should be the same as the delayed time of A (t_A’) observed by B at the same time t.
在我们的方法中，两个观察者（A 和 B）在时间 t = 0 时以相同的速度（v/2）从见证者（W）向相反方向出发，其中 v 是 A 和 B 相互分离的速度。在这种配置中，A 在时间 t 观察到的 B 的延迟时间（t_B’）应该与 B 在同一时间 t 观察到的 A 的延迟时间（t_A’）相同。

Now we analyze both methods of light propagation between both observers (A and B). In the first, no medium is needed, and light travels in ballistic mode. In the second, we assume the existence of a luminiferous medium (ether) where light travels like a wave.
现在我们分析两个观察者（A 和 B）之间光传播的两种方法。第一种方法不需要介质，光以弹道模式传播。第二种方法，我们假设存在光以太介质（ether），光在其中像波一样传播。

Light propagation in ballistic mode

光以弹道模式传播

In this way of propagation, no ether is used, and light travels in a ballistic mode. The wavefront travels at speed c in the originating frame of reference; for instance, light wavefronts departing from A (shown as blue circles in Fig. 3 and as blue lines in Fig. 4) have speed c at A’s frame of reference. The witness W at the midpoint, however, would see both (blue and orange) transmitted signals passing at speed c - v/2 in opposite directions, as shown in Fig. 3, Fig. 4:
在这种传播方式中，不使用以太，光以弹道模式传播。波前在起始参考系中以速度 c 传播；例如，从 A 出发的光波前（如图 3 中的蓝色圆圈和图 4 中的蓝色线条所示）在 A 的参考系中具有速度 c。然而，中点的见证者 W 会看到两个（蓝色和橙色）传输信号以速度 c - v/2 沿相反方向通过，如图 3、图 4 所示：

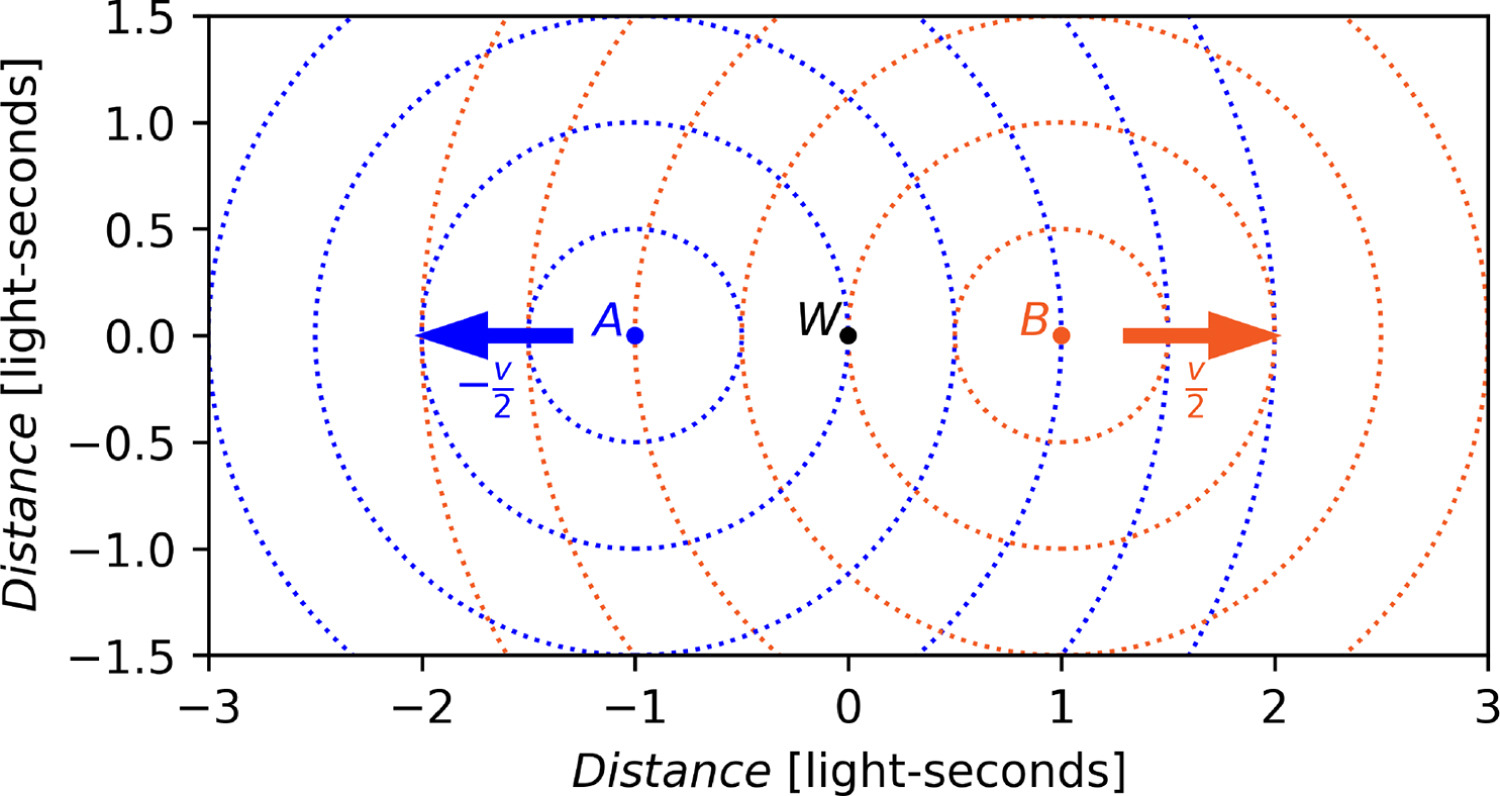
Figure 3. Ballistic light wavefronts (blue and orange dotted circles) emitted by two observers (A and B, respectively) that are departing from W at $u/2$ in opposite directions.

图 3. 两名观察者（A 和 B）分别以 $u/2$ 的速度从 W 点向相反方向出发时，以球形波前形式发出的光（蓝色和橙色虚线圆圈）。

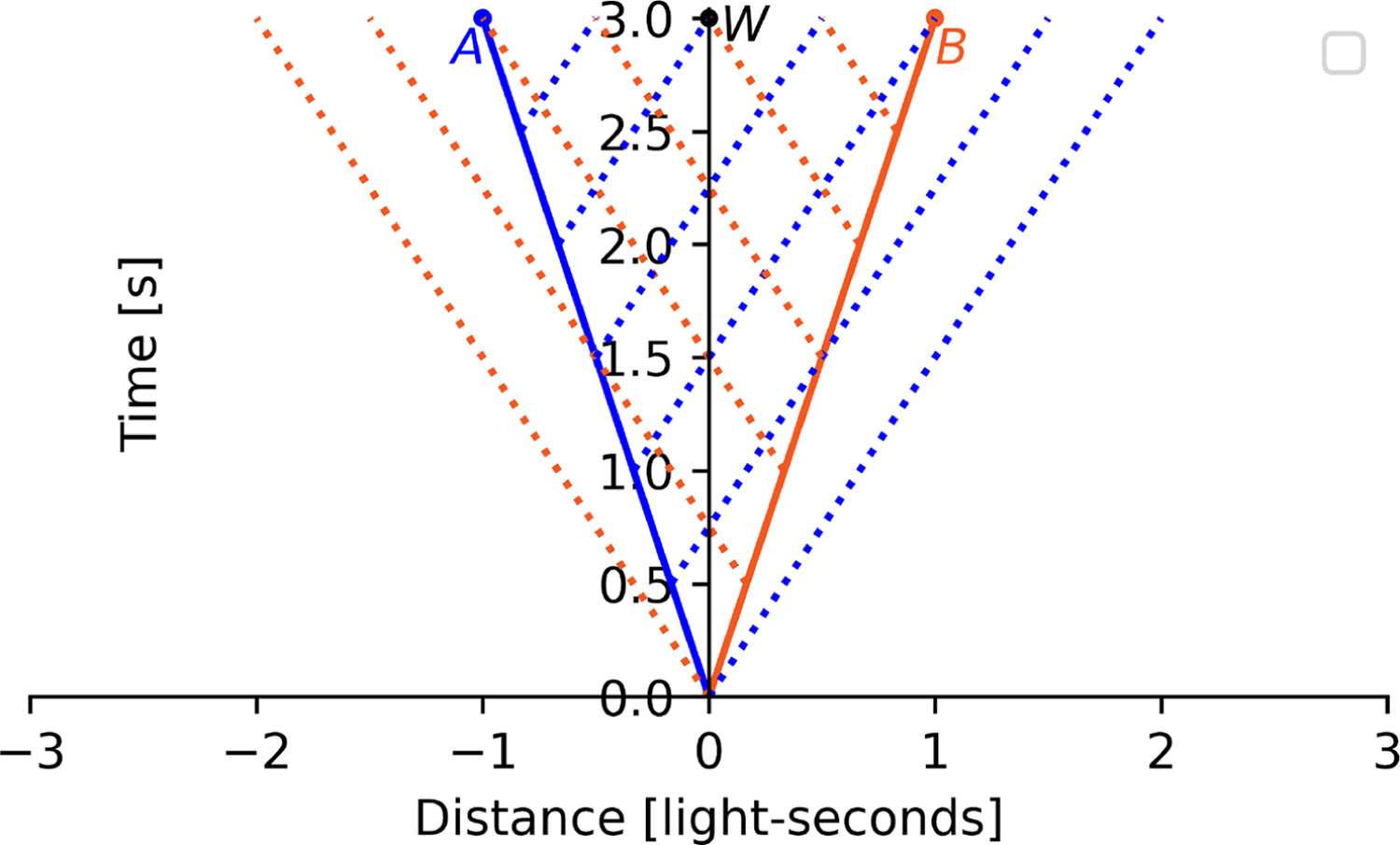
Figure 4. Time vs. Distance representation of the wavefronts of Figure 3. The light wavefronts departing from A and B are shown with blue and orange dotted lines, respectively.
图 4. 图 3 中波前的时间与距离表示。从 A 和 B 发出的光波前分别用蓝色和橙色虚线表示。

By applying the classical Doppler effect formula with these conditions, we have
通过在这些条件下应用经典多普勒效应公式，我们有
$$f_r=f_t\left(\frac{(c-v/2)+v_r}{(c-v/2)+v_t}\right)\text{\hspace{1em}(15)}$$
where $f_r$ denotes the received frequency and f_t is the transmitted frequency.

其中 $f_r$ 表示接收频率，$f_t$ 是发射频率。

If we use this formula to estimate the parallel and anti-parallel frequencies (f_p, f_a) observed in the Ives-Stilwell experiments, we obtain:
如果我们使用这个公式来估计在艾夫斯-斯蒂尔韦尔实验中观察到的平行和反平行频率（f_p, f_a），我们得到：
$$f_p=f_s\left(\frac{(c-v/2)-v/2}{(c-v/2)+v/2}\right)=f_s\left(\frac{c-v}{c}\right)\text{\hspace{1em}(16)}$$
$$f_a=f_s\left(\frac{(c+v/2)+v/2}{(c+v/2)-v/2}\right)=f_s\left(\frac{c+v}{c}\right)\text{\hspace{1em}(17)}$$
However, these estimations of $f_p,f_a$ do not satisfy $Eq.(14)$, observed in the Ives-Stilwell experiments:
然而，这些 $f_p、f_a$ 的估计不满足艾夫斯-斯蒂尔韦尔实验中观察到的方程（14）：
$$f_a{f}_p=f_{src}^2\left(\frac{c+v}{c}\right)\left(\frac{c-v}{c}\right)\ne f_{src}^2\text{\hspace{1em}(18)}$$
which means that light does not propagate in ballistic mode in the Ives-Stilwell experiment.
这意味着在艾夫斯-斯蒂尔韦尔实验中，光不以弹道模式传播。

Light propagation through a luminiferous medium (ether)

通过光以太介质（ether）的光传播

For this method of propagation, a luminiferous medium is included, which is assumed to be at rest with respect to the witness W’s frame of reference to warrant symmetry. Fig. 5, Fig. 6 show the light wavefronts departing from A (shown as blue circles in Fig. 5 and as blue lines in Fig. 6). This time, the witness W would see the transmitted signals (blue and orange) transiting at speed c in opposite directions, as shown in Fig. 5, Fig. 6:
对于这种传播方法，包括光以太介质，假设该介质相对于见证者 W 的参考系静止，以保证对称性。图 5、图 6 显示了从 A 出发的光波前（如图 5 中的蓝色圆圈和图 6 中的蓝色线条所示）。这一次，见证者 W 会看到传输信号（蓝色和橙色）以速度 c 沿相反方向传输，如图 5、图 6 所示：

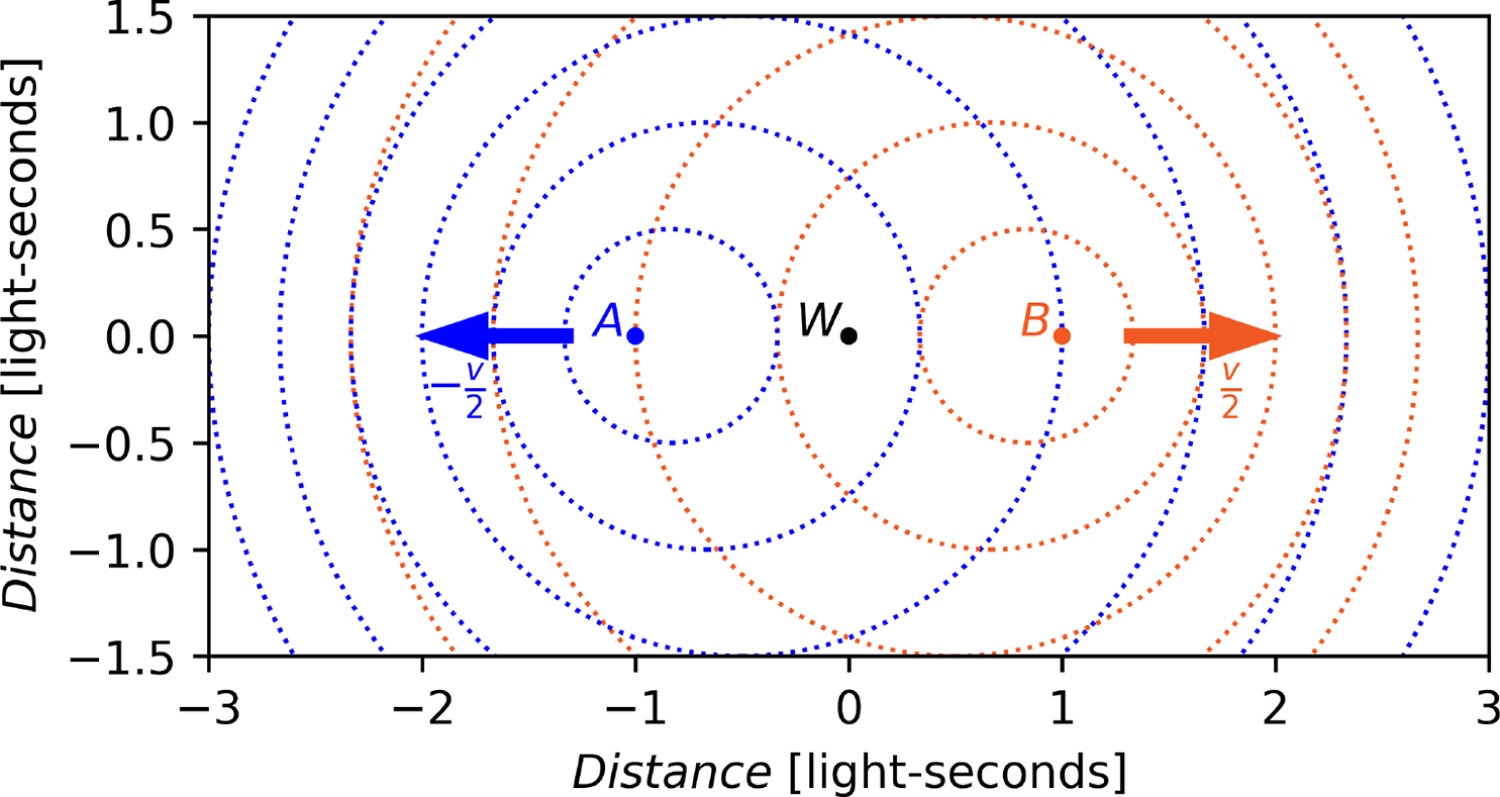
Figure 5. Light wavefronts (blue and orange dotted circles) emitted by two observers (A and B, respectively) that are departing from W at $u/2$ in opposite directions. The light waves propagate through a medium that is at rest with respect to W.
图 5.两名观察者（A 和 B）分别以 $u/2$ 的速度从 W 点向相反方向出发时，光通过介质传播的波前（蓝色和橙色虚线圆圈）。

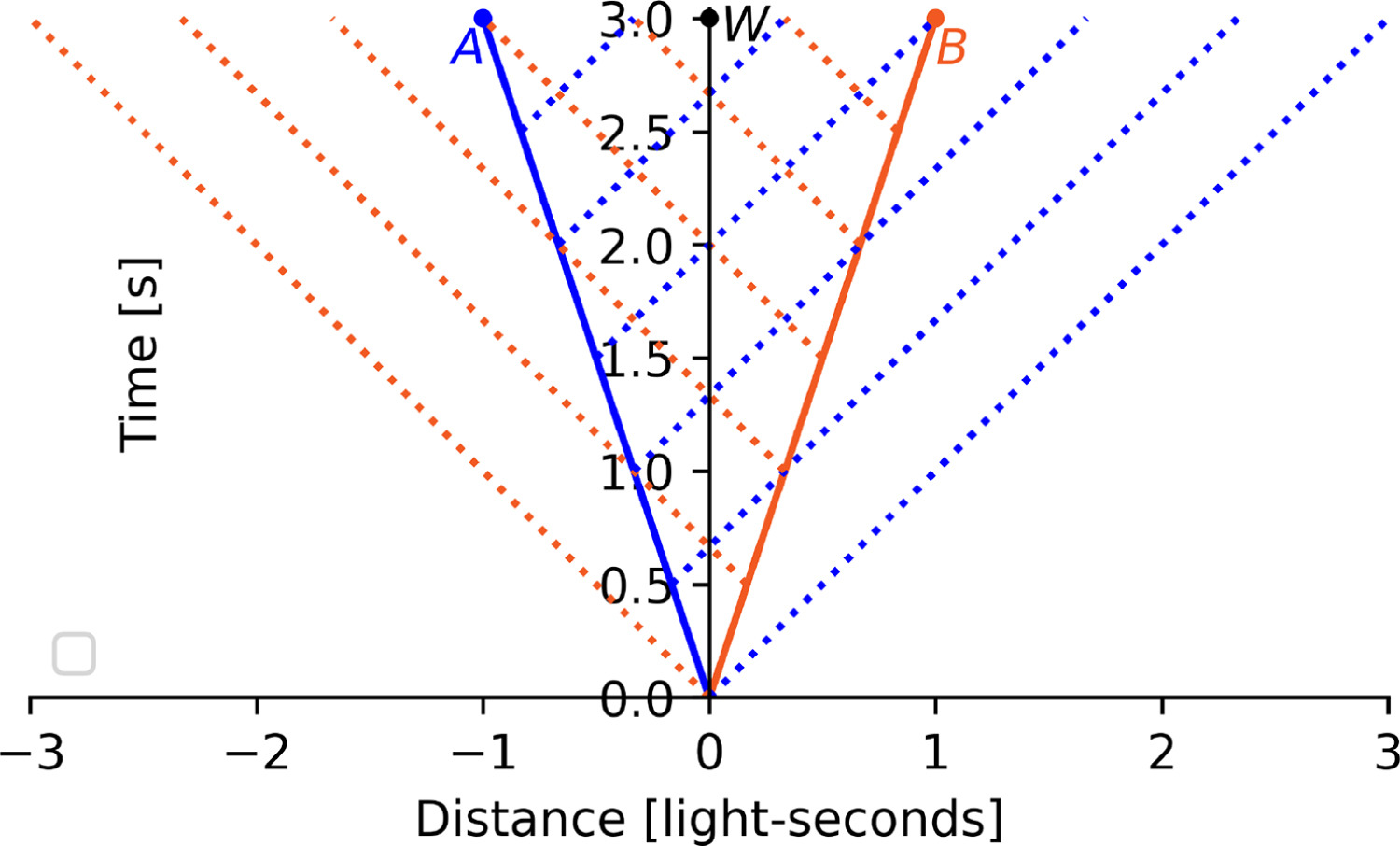
Figure 6. Time vs. Distance representation of the wavefronts of Figure 5. The light wavefronts departing from A and B are shown with blue and orange dotted lines, respectively.
图 6.图 5 中波前的时间与距离表示。从 A 和 B 发出的光波前分别用蓝色和橙色虚线表示。

If we apply the Doppler effect formula, the observed frequency would be given by:
如果我们应用多普勒效应公式，观察到的频率将由下式给出：
$$f_r=f_t\left(\frac{c+v_r}{c+v_t}\right)\text{\hspace{1em}(19)}$$
where $f_r$ and $f_t$ denote the received and transmitted frequencies, respectively.
其中 $f_r$ 和 $f_t$ 分别表示接收频率和发射频率。

If we use this formula to compute the parallel and anti-parallel frequencies ($f_a,f_p$), we obtain:
如果我们使用这个公式来计算平行和反平行频率（$f_a,f_p$），我们得到：
$$f_a=f_{src}\left(\frac{c+v_r}{c+v_t}\right)=f_{src}\left(\frac{c+v/2}{c-v/2}\right)=f_{src}\vartheta \text{\hspace{1em}(20)}$$
$$f_p=f_{src}\left(\frac{c+v_r}{c+v_t}\right)=f_{src}\left(\frac{c-v/2}{c+v/2}\right)=f_{src}/\vartheta \text{\hspace{1em}(21)}$$
where ϑ is (\vartheta = (c + v/2)/(c - v/2)). The wavelengths λ_a and λ_p are given by:
其中 ϑ 是 (\vartheta = (c + v/2)/(c - v/2))。波长 λ_a 和 λ_p 由下式给出：
$${\lambda }_a={\lambda }_{src}/\vartheta \text{\hspace{1em}(22)}$$
$${\lambda }_p={\lambda }_{src}\vartheta \text{\hspace{1em}(23)}$$

If we multiply f_a f_p, Eq. (14) is satisfied, in agreement with the Ives-Stilwell experiments:
如果我们将 f_a f_p 相乘，方程（14）得到满足，与艾夫斯-斯蒂尔韦尔实验一致：
$$f_a{f}_p=f_{src}\left(\frac{c-v/2}{c+v/2}\right)f_{src}\left(\frac{c+v/2}{c-v/2}\right)=f_{src}\vartheta f_{src}/\vartheta =f_{src}^2\text{\hspace{1em}(24)}$$

We interpret this preliminary result as proof that light propagates as a wave in accordance with Maxwell’s prediction [6] and through a luminiferous medium (ether) as predicted by Doppler [23].
我们将这一初步结果解释为证明光按照麦克斯韦的预测 [6] 作为波传播，并通过多普勒 [23] 预测的光以太介质（ether）传播。

Procrustes’ Bed

普罗克鲁斯特斯床

A more detailed description is shown in Fig. 7, where we can identify three different medium regions limited by the white dashed lines: the observer medium region (blue), the transmitter medium region (orange), and an intermediate medium region (color gradient) that we call the “Procrustean Bed” (PB), where there is a velocity gradient between the transmitter’s and the observer’s mediums (not-to-scale), similar to the velocity gradient along the sections of a stretching rubber band as shown in Fig. 8. In the PB, light is dragged by the medium speed gradient, which increases or decreases the light velocity so that the speed of light within each different medium remains constant when transiting it. As a result, light’s wavelength and period are stretched or contracted. The plot shows a smooth transit of light (yellow line) during its passage in the PB that may change depending on how the different mediums interact. In our approach, we use the average light speed shown by the dashed yellow line. Notice that if the relative speed between the observer’s and the transmitter’s mediums is zero, the PB is not created. However, even if the observer and transmitter are in the same frame of reference, the speed of light could vary in its transit if there are other intermediate varying speed mediums (not shown).
更详细的描述如图 7 所示，我们可以在图中识别出由白色虚线限定的三个不同介质区域：观察者介质区域（蓝色）、发射体介质区域（橙色）和一个中间介质区域（颜色渐变），我们称之为“普罗克鲁斯特斯床”（PB），其中发射体和观察者的介质之间存在速度梯度（不按比例），类似于图 8 所示的拉伸橡皮筋各部分的速度梯度。在 PB 中，光被介质速度梯度拖动，该梯度增加或减少光速，使得光在每个不同介质中传输时速度保持恒定。结果，光的波长和周期被拉伸或收缩。该图显示了光（黄色线）在 PB 中通过时的平滑传输，这可能会根据不同介质的相互作用方式而变化。在我们的方法中，我们使用虚线黄色线所示的平均光速。请注意，如果观察者和发射体的介质之间的相对速度为零，则不会创建 PB。然而，即使观察者和发射体处于同一参考系中，如果存在其他中间变速介质（未显示），光的传播速度也可能在其传输过程中发生变化。

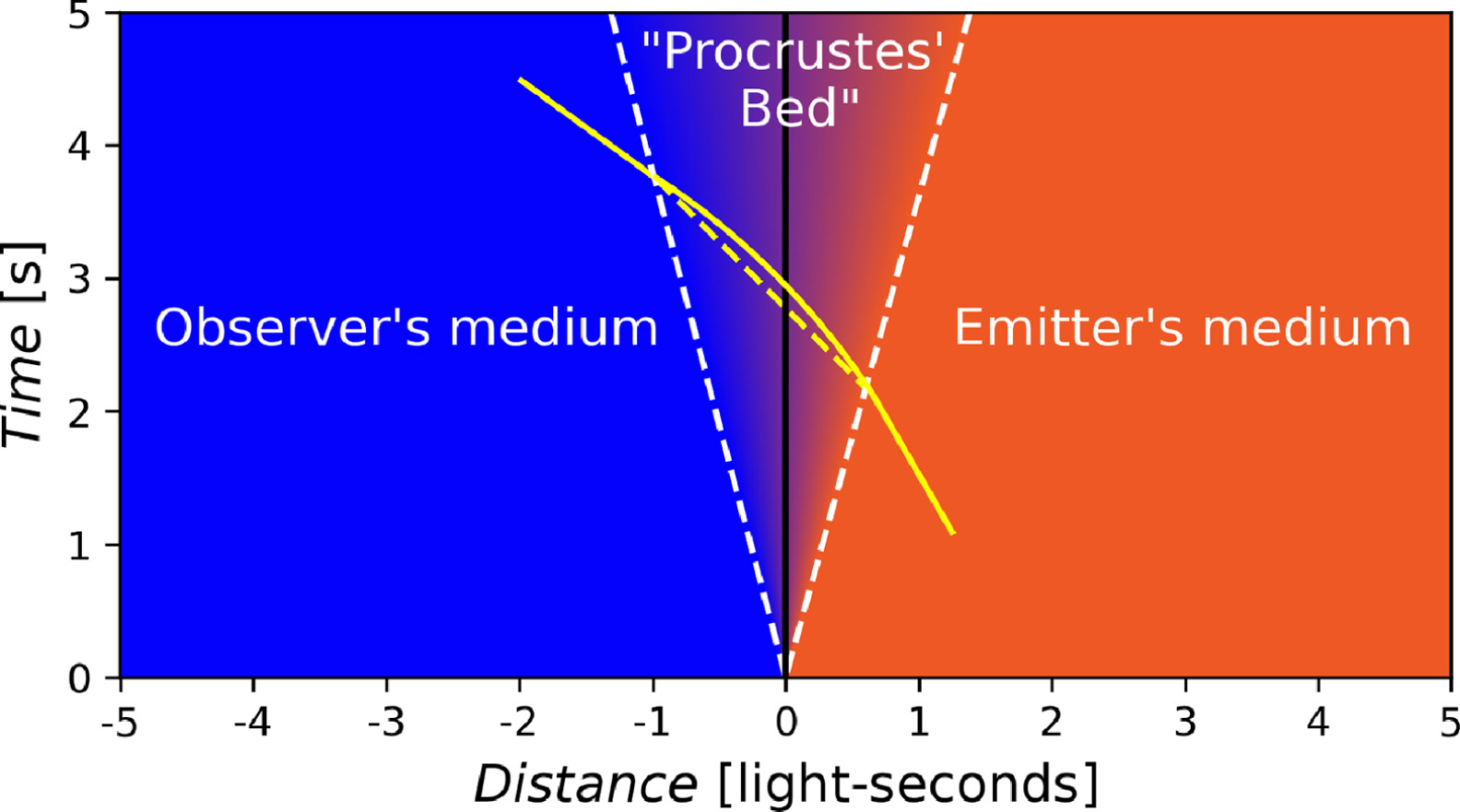
Figure 7. At the Bed of Procrustes, light is dragged by the velocity gradient between the transmitter’s (orange) and the observer’s (blue) mediums, resulting in the stretching or contraction of the wavelength. Notice how light maintains its relative constant speed $c$ with respect to the different mediums when transiting them.
图 7.在普洛克鲁斯特之床上，光被发射器（橙色）和观察者（蓝色）介质之间的速度梯度拖动，导致波长拉伸或收缩。注意光在通过不同介质时保持相对恒定的速度 $c$。

Figure 8. At the Bed of Procrustes, the ether is stretched or contracted between the observer’s and the emitter’s mediums producing a velocity gradient of the ether similar to the velocity gradient along the sections of a stretching rubber band. The dashed lines indicate the constant velocities of the different sections of the rubber along the time with respect to the center, and they also have different colors to mimic the velocity gradient of Figure 7.
图 8.在普洛克鲁斯特之床上，以太在观察者和发射器介质之间被拉伸或压缩，产生类似于拉伸橡皮筋各部分的速度梯度。虚线表示橡皮筋各部分相对于中心的恒定速度，它们还用不同颜色来模拟图 7 中的速度梯度。

An equivalent representation for the PB of Fig. 7 is shown in Fig. 9, where coordinates are seen from the observer’s point of view, which will help us derive equations to transform observed and actual transmitter coordinates. In the plot, the blue and orange bold lines represent the space-time paths of the observer (blue star) and the transmitter (orange star), respectively, here the transmitter departs from the observer at a speed v. The dashed blue and orange lines are the limits of the PB (explained in Fig. 7). x₀ and x₁ represent the distances of the transmitter and the observer, respectively, to the PB limits, which in this example are assumed to be constant (constant segments depending on x₀ and x₁ are shown in black in the plot). t₀ = x₀/c and t₁ = x₁/c are the time that light requires to transit distances x₀ and x₁, respectively. The dotted orange lines represent periodic light signals departing from the transmitter, where the bold dotted orange line is a signal emitted when the transmitter was at (x’, t’) (hollow orange start) and received by the observer at time t when the transmitter was at (x, t) (orange start).
图 9 显示了图 7 中 PB 的等效表示，其中坐标是从观察者的角度来看的，这将帮助我们推导出转换观察到的和实际发射体坐标的方程。在图中，蓝色和橙色粗线分别表示观察者（蓝色星）和发射体（橙色星）的时空路径，这里发射体以速度 v 离开观察者。蓝色和橙色虚线是 PB 的边界（如图 7 所示）。x₀ 和 x₁ 分别表示发射体和观察者到 PB 边界的距离，在这个例子中，假设它们是恒定的（取决于 x₀ 和 x₁ 的恒定段在图中以黑色显示）。t₀ = x₀/c 和 t₁ = x₁/c 分别是光传输距离 x₀ 和 x₁ 所需的时间。橙色虚线表示从发射体出发的周期性光信号，其中粗橙色虚线是发射体在 (x’, t’)（空心橙色起点）时发射并在发射体在 (x, t)（橙色起点）时由观察者在时间 t 接收的信号。

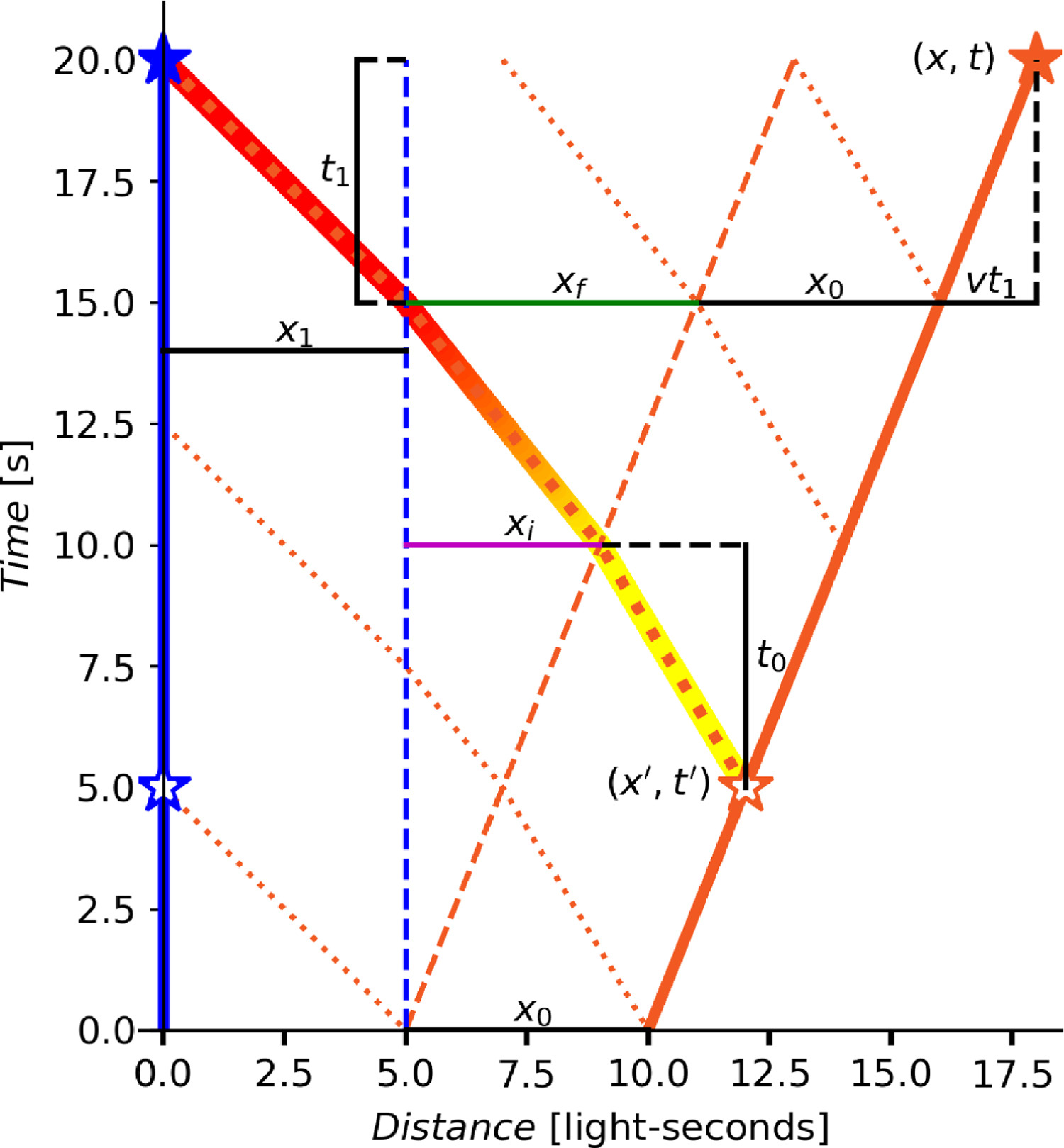
Figure 9. An example of the Procrustean Bed seen from the observer’s point of view. The blue and orange bold lines represent the space-time paths of the observer (blue star) and the transmitter (orange star), respectively. The line changing color from yellow to red illustrates the changing frequency of the light signal emitted at ($a^{\prime }$, $t^{\prime }$) during its transit at the emitter’s, the PB’s, and the observer’s mediums.
图 9.从观察者视角看到的普洛克鲁斯特之床示例。蓝色和橙色粗线分别表示观察者（蓝色星）和发射器（橙色星）的时空路径。颜色从黄变红的线表示光信号在发射器、PB 和观察者介质中传播时频率的变化。

Notice how the emitted light signals travel with respect to the observer at $c-u$ while transiting the transmitter’s medium, then at an average $c-u/2$ while transiting the PB, and at $c$ while transiting the observer’s medium. Whereas, with respect to the emitter (see Fig.10), the same emitted light signals travel at $c$ while transiting the emitter’s medium, then at an average $c+u/2$ while transiting the PB, and at $c+u$ while transiting the observer’s medium. The frequency change (red-shift) of the light signal emitted at ($a^{\prime }$, $t^{\prime }$) during its transit at the emitter’s, the PB’s, and the observer’s mediums is illustrated by the line changing color from yellow to red.

注意，发射的光信号在通过发射器介质时相对于观察者以 $c-u$ 的速度传播，然后在通过 PB 时以平均 $c-u/2$ 的速度传播，而在通过观察者介质时以 $c$ 的速度传播。然而，从发射器的角度来看（见图 10），相同的发射光信号在通过发射器介质时以 $c$ 的速度传播，然后在通过 PB 时以平均 $c+u/2$ 的速度传播，而在通过观察者介质时以 $c+u$ 的速度传播。光信号在发射器、PB 和观察者介质中传播时的频率变化（红移）由从黄色变为红色的线条表示。

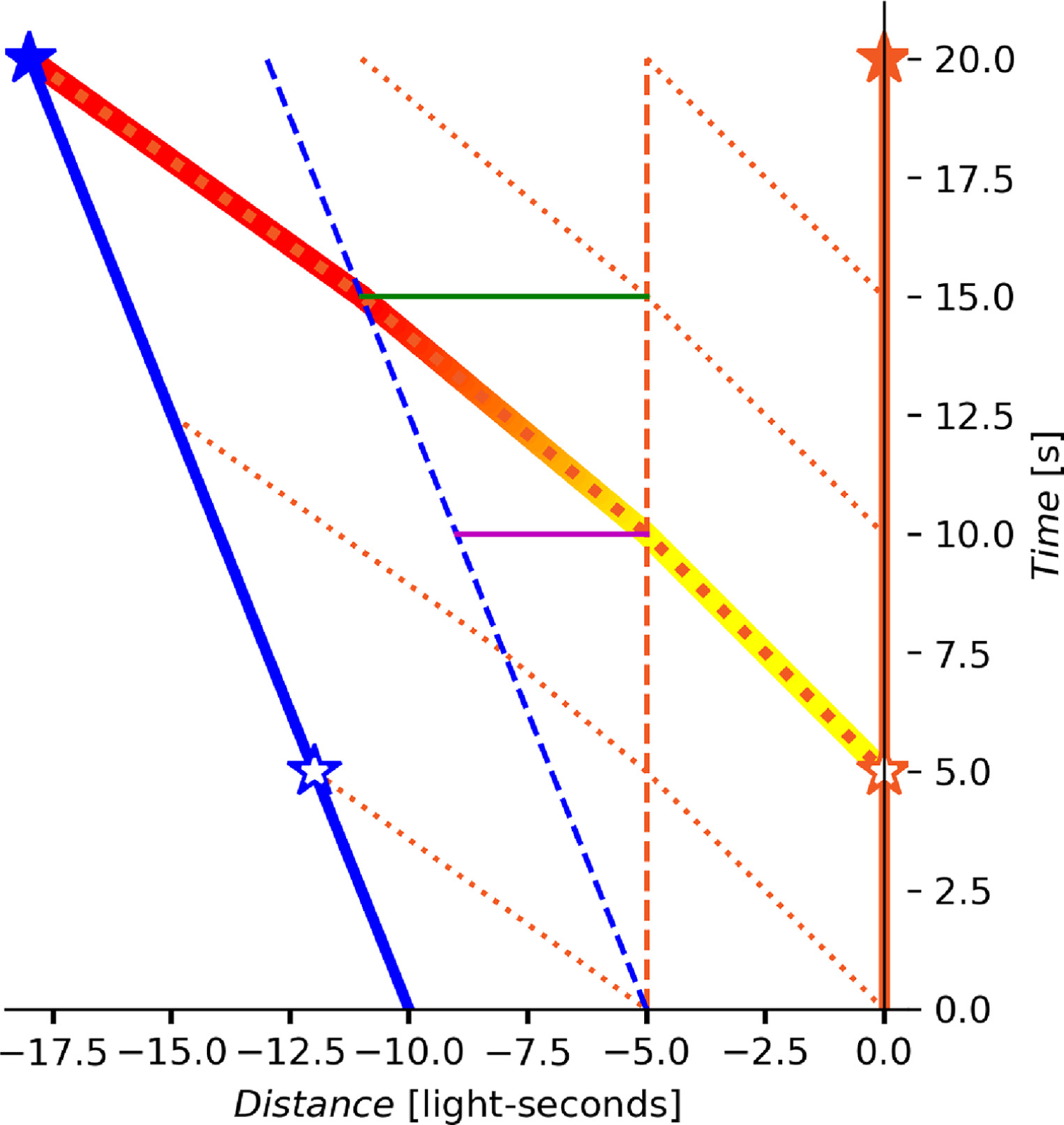
From the plot of Fig. 9, t₀ = x₀/c, t₁ = x₁/c, c_i = v(t’ + t₀) = (x’ - x₁) - (c - v)t₀ and by using the Theseus factor from Eqs. (20) and (23), x_f = ϑ x_i, t = ϑ(t’ + t₀) + t₁. The Procrustean transformation (PT) equations are:
从图 9 的图中，t₀ = x₀/c，t₁ = x₁/c，c_i = v(t’ + t₀) = (x’ - x₁) - (c - v)t₀，并使用方程（20）和（23）中的忒修斯因子，x_f = ϑ x_i，t = ϑ(t’ + t₀) + t₁。普罗克鲁斯特斯变换（PT）方程为：
$$t=\vartheta (t^{\prime }+t_0)+t_1\text{\hspace{1em}(25)}$$
$$x=vt+x_0+x_1\text{\hspace{1em}(26)}$$
or
$$x=x_f+v{t}_1+x_0+x_1\text{\hspace{1em}(27)}$$
$$x=\vartheta (x^{\prime }-x_1-(c-v)t_0)+v{t}_1+x_0+x_1\text{\hspace{1em}(28)}$$

When deriving Eqs. (25), (28), we have:
在推导方程 (25), (28) 时，我们有：
$$dt=\vartheta d{t}^{\prime }\text{\hspace{1em}(29)}$$
$$dx=\vartheta d{x}^{\prime }\text{\hspace{1em}(30)}$$
which means that the rate of change of the length and period of a light wave are independent on x₀ and x₁, and we can use the simple Eqs. (20)-(23) for their estimations:
这意味着光波的波长和周期的变化率与 x₀ 和 x₁ 无关，我们可以使用简单的方程（20）-（23）来估计它们：
$$\lambda =\vartheta {\lambda }^{\prime }\text{\hspace{1em}(31)}$$
$$\tau =\vartheta {\tau }^{\prime }\text{\hspace{1em}(32)}$$
$$f=f^{\prime }/\vartheta \text{\hspace{1em}(33)}$$

The wave speed in the transmitter’s medium is given by
发射体介质中的波速由下式给出
$$v^{\prime }={\lambda }^{\prime }/{\tau }^{\prime }=c\text{\hspace{1em}(34)}$$
whereas, in the observer’s medium the wave speed is given by
而在观察者介质中，波速由下式给出
$$v=\lambda /\tau =(\vartheta {\lambda }^{\prime })/(\vartheta {\tau }^{\prime })=c\text{\hspace{1em}(35)}$$

Therefore, the wave speed remains constant with respect to each medium while transiting them as predicted by Maxwell [6]. However, the wave speed does not necessarily remain constant with respect to the different frames of reference as shown in Fig. 11, where the frequency and wavelength of the emitted wave-light at the top of the figure remain unchanged during its transit at the common medium of the emitter and the observer, the wave-light in the middle is stretched (red-shifted) at the PB, increasing its wavelength and speed, and the wave-light at the bottom of the figure is contracted (blue-shifted) at the PB, decreasing its wavelength and speed. In all three cases, the wave-light departs at a speed c with respect to the emitter and arrives at a speed c with respect to the observer. The changing color of the wave-light represents the observed frequencies at the different transited mediums.
因此，正如麦克斯韦 [6] 所预测的那样，波速在通过每个介质时相对于每个介质保持恒定。然而，如图 11 所示，波速相对于不同的参考系不一定保持恒定，图中顶部发射的光波在发射体和观察者的共同介质中传输时频率和波长保持不变，中间的光波在 PB 处被拉伸（红移），增加了其波长和速度，图底部的光波在 PB 处被压缩（蓝移），降低了其波长和速度。在所有三种情况下，光波相对于发射体以速度 c 离开，相对于观察者以速度 c 到达。光波颜色的变化代表了在不同传输介质中观察到的频率。

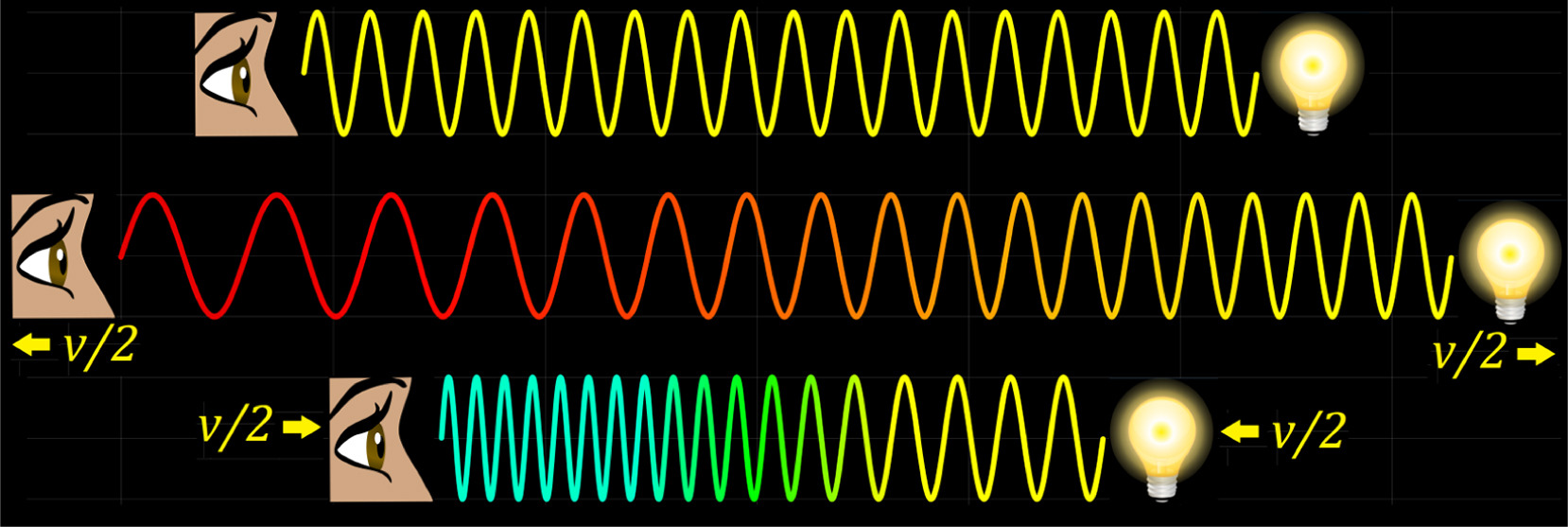
Figure 11. An illustration of the change of the wavelength and speed of a wave-light in the Procrustean Bed due to the relative motion between the emitter and the observer. See text for details.
图 11.由于发射器和观察者之间的相对运动，在普洛克鲁斯特之床中光的波长和速度的变化示意图。见正文详细描述。

These effects are counterintuitive if we think of light as a particle, i.e. if the source is approaching the observer, the light front should be faster. SR would tell us that the light front speed should be constant. However, here we show that, as a wave, light is slowed by the PB when the source approaches the observer. It makes more sense if we think that a wave, as an energy carrier, will increase its frequency by giving up speed, or it will increase its speed by decreasing its frequency.
如果我们将光视为粒子，即如果源正在接近观察者，光前应该更快，这些效应就会违反直觉。狭义相对论会告诉我们，光前速度应该是恒定的。然而，这里我们表明，作为波，当源接近观察者时，光会被 PB 减慢。如果我们认为波作为能量载体，会通过放弃速度来增加频率，或者通过降低频率来增加速度，这就更有意义了。

Note that the configuration used to derive these PT equations is just an example to introduce the PB concept, and that is one of number of possible configurations between an emitter, an observer, and a dynamic medium.
请注意，用于推导这些 PT 方程的配置只是引入 PB 概念的一个例子，并且是发射体、观察者和动态介质之间可能的配置之一。

Average observed frequency

平均观察频率

In Section “Light propagation through a luminiferous medium (ether)”, we averaged the observer and transmitter medium speeds to determine the relation between the observed and emitted frequencies. If, instead, we use the average of the observed frequencies when the medium is at rest with respect to the observer and transmitter, using the CDE, the average observed frequency (AOF) would be given by:
在“通过光以太介质（ether）的光传播”部分，我们对观察者和发射体介质速度进行了平均，以确定观察到的频率和发射频率之间的关系。相反，如果我们使用当介质相对于观察者和发射体静止时观察到的频率的平均值，使用经典多普勒效应，平均观察频率（AOF）将由下式给出：
$$f_r=\frac{f_t(c/(c+v_t))+f_t((c+v_r)/c)}{2}\text{\hspace{1em}(36)}$$
where f_r and f_t denote the received and transmitted frequencies, respectively.
其中 $f_r$ 和 $f_t$ 分别表示接收频率和发射频率。

If we use this formula to compute the parallel and antiparallel frequencies ($f_a,f_p$), we obtain:
如果我们使用这个公式来计算平行和反平行频率（$f_a,f_p$），我们得到：
$$f_a=\frac{f_t(c/(c-v))+f_t((c+v)/c)}{2}\text{\hspace{1em}(37)}$$
$$f_p=\frac{f_t(c/(c+v))+f_t((c-v)/c)}{2}\text{\hspace{1em}(38)}$$

Although, these values are very similar to the corresponding RDE estimates, especially for |v| < ~0.5c (see Table 2 and Fig. 12), they do not satisfy Eq. (14), in disagreement with the Ives-Stilwell experiments.
尽管这些值与相应的相对论多普勒效应估计值非常相似，尤其是对于 |v| < ~0.5c（见表 2 和图 12），但它们不满足方程（14），与艾夫斯-斯蒂尔韦尔实验不一致。

Table 2. RDE, PT and AOF observed frequency estimations for v ranging from -0.35c to 0.35c.
表 2. v 范围从 -0.35c 到 0.35c 时 RDE、PT 和 AOF 观察频率估计值。

β(v/c)	f_RDE [Hz]	f_PT [Hz]	% diff	f_AOF [Hz]	% diff
-0.35	1.44115	1.42424	1.18737	1.44423	0.21354
-0.3	1.36277	1.35294	0.72650	1.36429	0.11120
-0.25	1.29099	1.28571	0.41068	1.29167	0.05207
-0.2	1.22474	1.22222	0.20640	1.22500	0.02083
-0.15	1.16316	1.16216	0.08586	1.16324	0.00647
-0.1	1.10554	1.10526	0.02519	1.10556	0.00126
-0.05	1.05131	1.05128	0.00313	1.05132	0.00008
0	1.00000	1.00000	0.00000	1.00000	0.00000
0.05	0.95119	0.95122	-0.00313	0.95119	0.00008
0.1	0.90453	0.90476	-0.02519	0.90455	0.00126
0.15	0.85973	0.86047	-0.08579	0.85978	0.00647
0.2	0.81650	0.81818	-0.20597	0.81667	0.02083
0.25	0.77460	0.77778	-0.40900	0.77500	0.05207
0.3	0.73380	0.73913	-0.72126	0.73462	0.11120
0.35	0.69389	0.70213	-1.17343	0.69537	0.21354

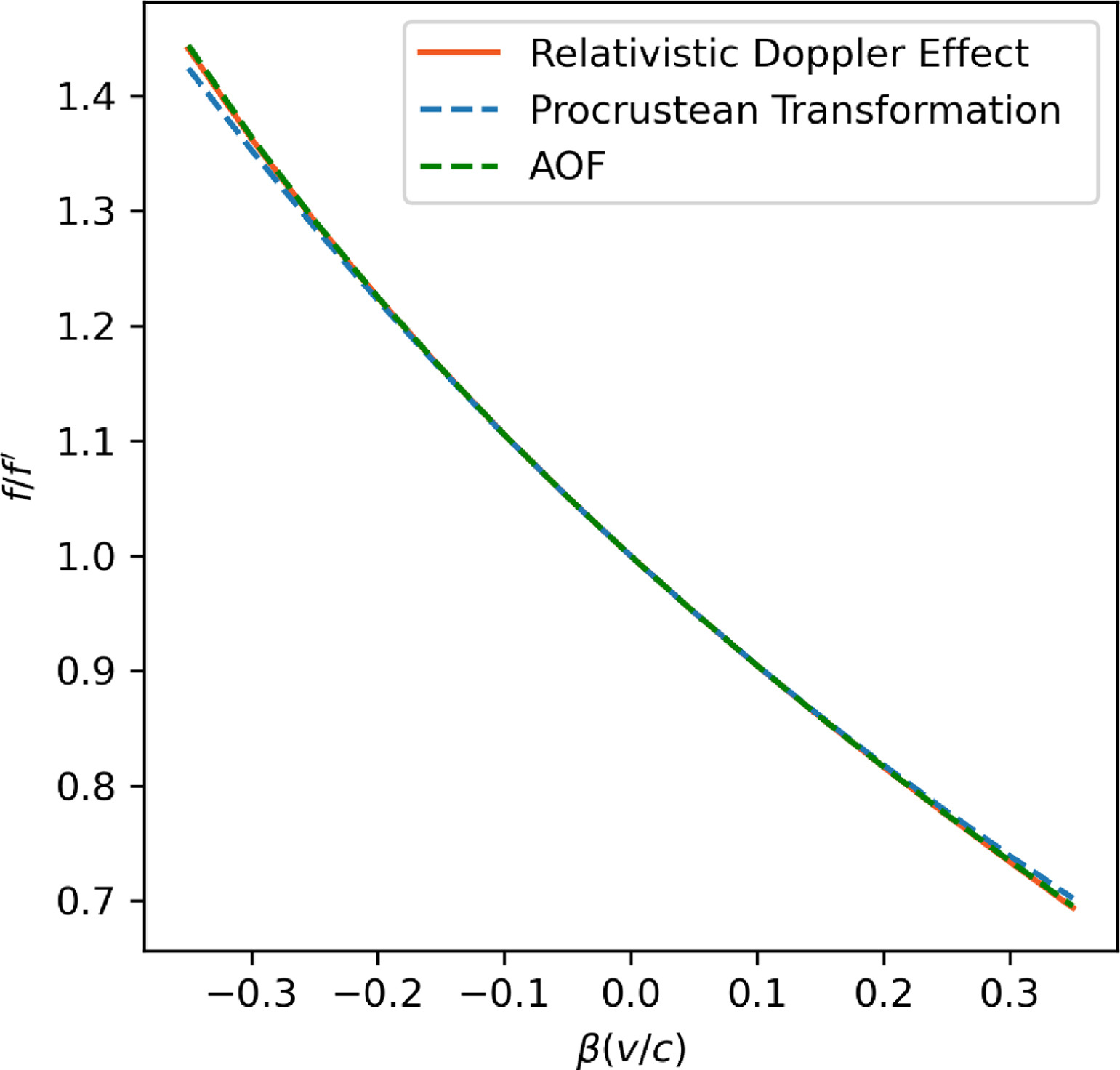
Figure 12. RDE, PT, and AOF observed frequency ratio estimates of a moving periodic signal. β ranges from -0.35 to 0.35.
图 12.相对论多普勒效应（RDE，橙色）、普洛克鲁斯特变换（PT，虚线蓝色）和平均观测频率（AOF，虚线绿色）对移动周期性信号的观测频率比估计值。β 的范围从 -0.35 到 0.35。

Results

结果

In general, Ives-Stilwell experiments compare the emitted frequency of a moving atomic clock with the geometric average of the parallel and anti-parallel observed frequencies given that the geometric average of the RDE estimations satisfies:
一般来说，艾夫斯-斯蒂尔韦尔实验将移动原子钟的发射频率与平行和反平行观察频率的几何平均值进行比较，因为相对论多普勒效应估计的几何平均值满足：
$$\surd (f_p{f}_a)=\surd (\surd ((1+\beta )/(1-\beta ))f_{src}\surd ((1-\beta )/(1+\beta ))f_{src})=\surd (f_{src}^2)=f_{src}\text{\hspace{1em}(39)}$$

The main advantage of using this equation is that there is no need to know the speed v of the moving atomic clock. Therefore, in the Ives-Stilwell experiments, the speed of the moving atomic clock is not directly measured. Instead, it is calculated through its kinetic energy [14] or its relativistic kinetic energy.
使用这个方程的主要优点是不需要知道移动原子钟的速度 v。因此，在艾夫斯-斯蒂尔韦尔实验中，移动原子钟的速度不是直接测量的。相反，它是通过其动能 [14] 或其相对论动能计算的。

With the PT estimations, the previous criteria is also satisfied:
通过 PT 估计，之前的标准也得到满足：
$$\surd (f_p{f}_a)=\surd (f_{src}((c-v/2)/(c+v/2))f_{src}((c+v/2)/(c-v/2)))=\surd (f_{src}^2)=f_{src}\text{\hspace{1em}(40)}$$

Therefore both approaches agree with the Ives-Stilwell experiments.
因此，这两种方法都与艾夫斯-斯蒂尔韦尔实验一致。

RDE and PT strongly agree when |v| < ~0.35c as in some Ives-Stilwell experiments [17, 18, 19].
正如一些艾夫斯-斯蒂尔韦尔实验 [17, 18, 19] 所示，当 |v| < ~0.35c 时，相对论多普勒效应和 PT 强烈一致。

Table 2 compares the estimations for the red-shifted (v > 0) and blue-shifted (v < 0) observed frequencies of a hypothetical 1 Hz moving clock with v ranging from -0.35c to 0.35c. We compare the three different approaches (RDE, PT, AOF). The first column shows the ratio v/c (β); the second, third, and fifth columns show the RDE, PT, and AOF frequency estimations, respectively, and the fourth and sixth columns show the percent differences between the RDE and PT estimations, and between the RDE and the AOF estimations, respectively.
表 2 比较了假设的 1 Hz 移动时钟在 v 范围从 -0.35c 到 0.35c 时红移（v > 0）和蓝移（v < 0）观察频率的估计值。我们比较了三种不同的方法（RDE、PT、AOF）。第一列显示比率 v/c（β）；第二、第三和第五列分别显示 RDE、PT 和 AOF 频率估计值，第四和第六列分别显示 RDE 和 PT 估计值之间以及 RDE 和 AOF 估计值之间的百分比差异。

In the plot of Fig. 12 from Table 2, we can see how the three (RDE in orange, PT in dashed blue, and AOF in dashed green) approaches almost agree in their observed frequency estimates when v ranges from -0.35c to 0.35c. RDE and PT approaches differ less than 1% for speeds -0.3c < v < 0.3c, whereas RDE and AOF approaches differ less than 0.12% in the same range of v. This result shows two possible alternative approaches for describing light physics up to ~30% the speed of light.
在表 2 的图 12 中，我们可以看到当 v 范围从 -0.35c 到 0.35c 时，三种方法（橙色的 RDE、蓝色虚线的 PT 和绿色虚线的 AOF）的观察频率估计几乎一致。对于速度 -0.3c < v < 0.3c，RDE 和 PT 方法的差异小于 1%，而在相同的 v 范围内，RDE 和 AOF 方法的差异小于 0.12%。这一结果显示了两种可能的替代方法，用于描述高达 ~30% 光速的光物理。

The plot of Fig. 13 is an extension of the plot of Fig. 12 with v ranging from -5c to 5c. Here we can see how the RDE observed frequencies are limited to the range -1c < v < 1c: whereas PT observed frequencies have no restrictions in v, allowing supraluminal velocities between the emitter and the observer. Notice, therefore, that the PT plot has two distinct features that are not presented in the RDE plot, where the observer receives negative frequencies.
图 13 的图是图 12 的扩展，v 范围从 -5c 到 5c。在这里我们可以看到相对论多普勒效应观察到的频率如何限制在 -1c < v < 1c 范围内：而 PT 观察到的频率在 v 上没有限制，允许发射体和观察者之间的超光速速度。因此，请注意，PT 图有两个 RDE 图中没有的不同特征，即观察者接收到负频率。

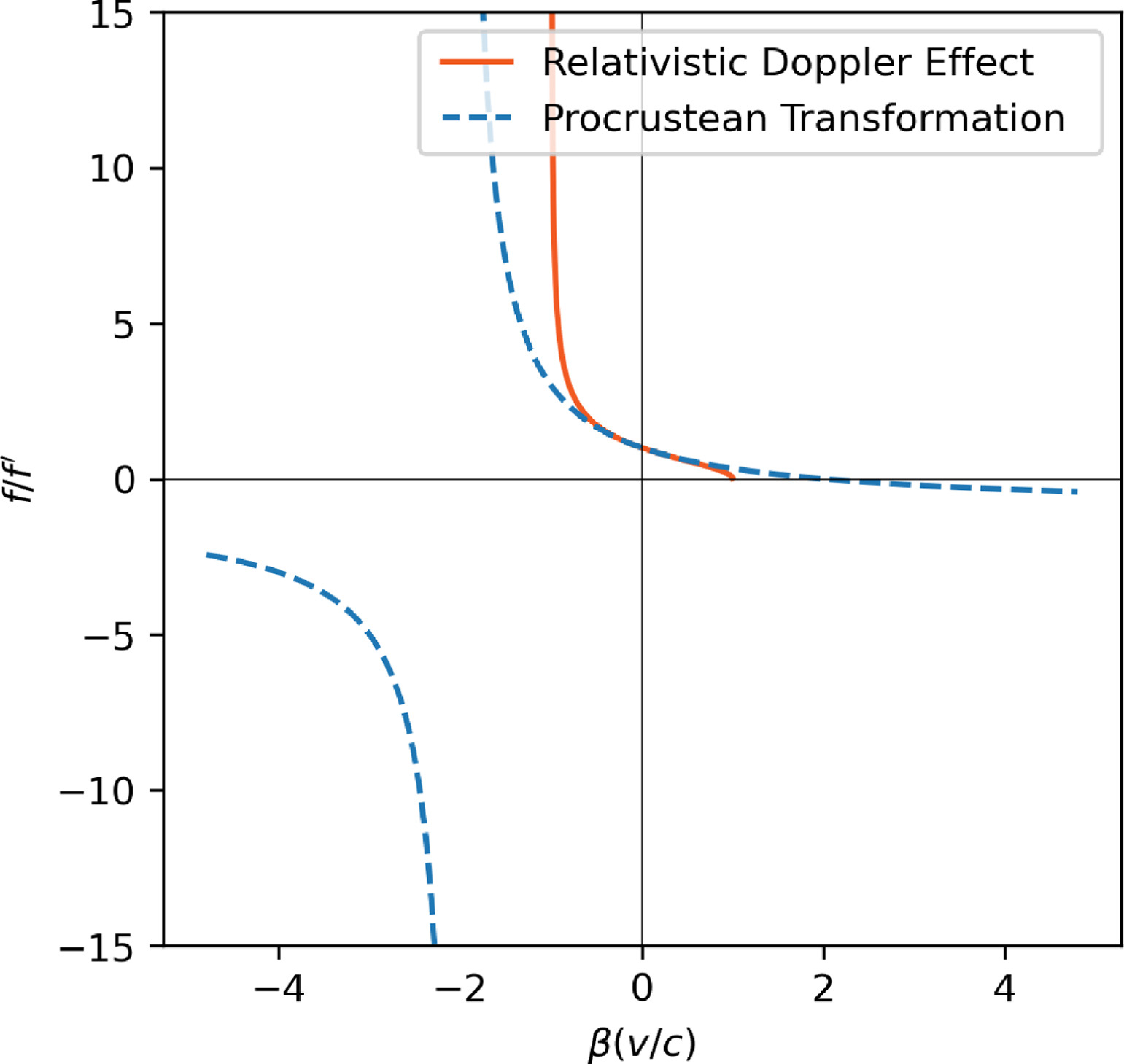
Figure 13. RDE and PT observed frequency ratio estimates of a moving periodic signal. β ranges from -5 to 5.
图 13.相对论多普勒效应（RDE）和普洛克鲁斯特变换（PT）对移动周期性信号的观测频率比估计值。β 的范围从 -5 到 5。

The first feature, at v = -2c, represents the point at which both, the emitter and the observer, reach the light barrier while approaching, i.e., both travel at speeds |v| = c with respect to the PB medium and where the frequency is so high (approaching infinite), that the light waves overlap producing a light boom, which is very similar to a sonic boom. This effect has been observed by Liang et al. [24] using ultra-fast video recording. If the observer is moving at v < -c with respect to the PB medium, it would observe the arrival of recently emitted signals followed by older ones (like watching a movie backwards), hence the negative frequency values.
第一个特征是在 v = -2c 处，表示发射体和观察者在接近时都到达光障的点，即两者相对于 PB 介质以 |v| = c 的速度行进，并且频率如此之高（接近无穷大），以至于光波重叠产生光爆，这与声爆非常相似。梁等人 [24] 使用超高速视频记录观察到了这种效应。如果观察者相对于 PB 介质以 v < -c 的速度移动，它将观察到最近发射的信号先到达，然后是较早的信号（就像倒放电影一样），因此出现负频率值。

The second feature at v = 2c shows the point at which both the emitter and the observer reach the speed of light with respect to the PB medium while departing from each other. Thus, the observer travels in the same direction and at the same speed as the emitter’s signals; therefore, no emitted frequency is detected. If the observer speed is higher than c with respect to the PB medium, it would be faster than the emitter’s signals, encountering them in reverse chronological order and appearing to come from the opposite direction of their origin at low frequencies. Observing this effect could be similar to what is known as cosmic background radiation [25]. This result is particularly important if we consider the possibility that gravitational wave signals travel similarly to lightwave signals, as observed by the LIGO and Virgo observatories [26]. In this case, an observer traveling in the same direction but faster than emitted gravitational waves would encounter them in reverse chronological order appearing to come from the opposite direction of their origin. This would create of a repulsive gravity that could contribute to the expansion of the universe [27].
v = 2c 处的第二个特征显示了发射体和观察者在相互离开时相对于 PB 介质都达到光速的点。因此，观察者与发射体的信号同向同速行进；因此，没有检测到发射频率。如果观察者相对于 PB 介质的速度高于 c，它将比发射体的信号更快，以逆时间顺序遇到它们，并在低频下似乎来自其起源的相反方向。观察这种效应可能类似于所谓的宇宙背景辐射 [25]。如果我们考虑到引力波信号的传播方式与光波信号相似的可能性，这一结果尤其重要，正如 LIGO 和 Virgo 天文台所观察到的 [26]。在这种情况下，一个沿相同方向但比发射的引力波更快的观察者将以逆时间顺序遇到它们，似乎来自其起源的相反方向。这将产生一种排斥性引力，可能有助于宇宙的膨胀 [27]。

Similar negative frequencies have been described by Shi et al. [28] for light waves in homogeneous systems with a positive refractive index.
史等人 [28] 对具有正折射率的均匀系统中的光波描述了类似的负频率。

Now, let’s imagine we can observe the time of a remote clock that is synchronized to our time, but at a distance d and a speed v = 0 with respect to ourselves. The observed time t’, according to PT, would be given by Eq. (25) as:
$$\vartheta (t^{\prime }+t_0)=t-t_1\text{\hspace{1em}(41)}$$
Where ϑ = (c + v/2)/(c - v/2) = 1 at v = 0. From Fig. 9:
$$t^{\prime }=t-(t_0+t_1)=t-(x_0+x_1)/c=t-d/c\text{\hspace{1em}(42)}$$
因此，观察到的时间 t’ 相对于我们的本地时间 t 会延迟光传播距离 d 到观察者所需的时间 (d/c)，这是有意义的。然而，这一结果与洛伦兹变换的估计不同，当 v = 0 时，方程（4）变为：
$$t^{\prime }{|}_{v=0}=\gamma (t-vx/c^2){|}_{v=0}=t\text{\hspace{1em}(43)}$$

Notice that PT does not become Galilean transformations when v → 0, as in the case of LT. However, both PT and LT become Galilean transformations when c → ∞.
请注意，与洛伦兹变换的情况不同，当 v → 0 时，PT 不会变成伽利略变换。然而，当 c → ∞ 时，PT 和 LT 都变成伽利略变换。

Discussion

讨论

The special theory of relativity, started by Poincaré and elaborated by Einstein, to interpret Lorentz mechanics has been accepted and used in a range of branches of physics because it has been demonstrated by several tests, including the Ives-Stilwell experiment. However, it still seems to conflict with some fundamental facts, such as the twin paradox and that the speed of light is the ultimate speed for physics [11]. In this paper, we propose an alternative to Lorentz transformations, Procrustean transformations, which confirm the wave nature of light and the need for a luminiferous medium (ether), where light waves are conditioned to travel at a specific constant speed as deduced by Maxwell [6].
由庞加莱开创并由爱因斯坦阐述的狭义相对论，用于解释洛伦兹力学，已被接受并应用于一系列物理分支，因为它已被包括艾夫斯-斯蒂尔韦尔实验在内的几项测试所证实。然而，它似乎仍然与一些基本事实相矛盾，例如双生子悖论和光速是物理学的终极速度 [11]。在本文中，我们提出了洛伦兹变换的替代方案，普罗克鲁斯特斯变换，它证实了光的波动性质和对光以太介质（ether）的需求，正如麦克斯韦 [6] 所推导的，光波在其中被限制以特定的恒定速度传播。

Our approach considers the existence of an absolute space and a universal time in which observations are always delayed due to the limited speed of light as the information carrier. Therefore, observations are always apparent and past versions of the observed objects, even when objects are not in relative motion with respect to the observer, as shown by Eq. (42), where observations are delayed by the time it takes to light to travel a distance d to the observer, i.e. d/c. LT, however, suggests that the observed times of objects not moving with respect to the observer always match the observer’s time regardless of the object’s distance (see Eq. (43)). In addition, LT cannot directly be used to determine the observed frequency change of a moving periodic signal, as originally suggested by Einstein, i.e. f_obs = f_src/γ [14]. Instead, it is necessary to use the RDE derived from the CDE applied to LT. In our approach, we can directly use the Theseus factor (ϑ) to determine the observed frequency of a moving periodic signal (See Eq. (20)), given that this factor is derived from a refined Doppler effect, which we call the PB, where light transits in a luminiferous medium at c as deduced by Maxwell [6]; however, the luminiferous medium undergoes a velocity gradient between the emitter and the observer (if they are in relative motion) and is at rest at each (see Fig. 7, Fig. 9), similar to some light-dragging theories such as Fizeau [29], Fresnel [30] and Huidobro et al. [31]. However, further research is needed to determine how the observer, emitter, and intermediate medium different configurations behave as their relative sizes and speeds change.
我们的方法考虑了绝对空间和通用时间的存在，其中由于光作为信息载体的速度有限，观察总是延迟的。因此，观察总是被观察物体的表观和过去版本，即使物体相对于观察者没有相对运动，如方程（42）所示，其中观察被光传播距离 d 到观察者所需的时间延迟，即 d/c。然而，洛伦兹变换表明，相对于观察者不移动的物体的观察时间总是与观察者的时间匹配，无论物体的距离如何（见方程（43））。此外，洛伦兹变换不能直接用于确定移动周期性信号的观察频率变化，正如爱因斯坦最初建议的那样，即 f_obs = f_src/γ [14]。相反，有必要使用从应用于洛伦兹变换的经典多普勒效应导出的相对论多普勒效应。在我们的方法中，我们可以直接使用忒修斯因子（ϑ）来确定移动周期性信号的观察频率（见方程（20）），因为这个因子是从改进的多普勒效应导出的，我们称之为 PB，正如麦克斯韦 [6] 所推导的，光在光以太介质中以 c 传播；然而，光以太介质在发射体和观察者之间经历速度梯度（如果它们处于相对运动中），并且在每个位置都是静止的（见图 7、图 9），类似于一些光拖曳理论，如菲佐 [29]、菲涅耳 [30] 和惠多布罗等人 [31]。然而，需要进一步的研究来确定观察者、发射体和中间介质的不同配置在它们的相对大小和速度变化时的行为。

Our approach closely agrees with the Ives-Stilwell experiment and the RDE in estimating the transmitted frequency by computing the geometric mean of the observed parallel and anti-parallel frequencies [17, 18, 19], as shown in Eqs. (12), (24). PT and RDE estimations of the observed parallel and anti-parallel frequencies, given the speed and frequency of a moving source, differ less than 1% at low speeds, up to 0.35c, as shown in Fig. 12. However, at higher speeds, the RDE estimations are mathematically restricted to v values ranging from -c to c, given that in both the RDE and γ, the square root of a negative value is indeterminate. However, PT has no mathematical restriction for values of v; i.e. PT allows supraluminal relative velocities between the emitter and the observer, as shown in Fig. 13. Supraluminal velocities have already been observed in relativistic jets [32].
我们的方法在通过计算观察到的平行和反平行频率的几何平均值来估计发射频率方面与艾夫斯-斯蒂尔韦尔实验和相对论多普勒效应密切一致 [17, 18, 19]，如方程（12）、（24）所示。如图 12 所示，给定移动源的速度和频率，PT 和 RDE 对观察到的平行和反平行频率的估计在高达 0.35c 的低速下差异小于 1%。然而，在较高速度下，相对论多普勒效应的估计在数学上限制在 v 值从 -c 到 c 的范围内，因为在相对论多普勒效应和 γ 中，负值的平方根是不确定的。然而，PT 对 v 的值没有数学限制；即 PT 允许发射体和观察者之间的超光速相对速度，如图 13 所示。超光速速度已经在相对论喷流中被观察到 [32]。

Without the speed restriction, an observer could travel through a medium containing the observer’s past light waves and even observe them in reverse order, which would appear both as seeing time backward and that the origin of the light waves is in front instead of at the back of the observer. If this effect is applied to gravity waves, given that light and gravity waves seem to travel similarly as demonstrated by the LIGO and VIGO observations [26], an observer traveling faster than light will observe gravity waves in reverse order, which will inverse the attraction force direction with respect to the origin of the waves. This effect could have an important contribution to the accelerated expansion of the universe [33, 34] that has been attributed to dark energy [27].
如果没有速度限制，观察者可以穿过包含观察者过去光波的介质，甚至可以逆序观察它们，这看起来既像是在倒着看时间，又像是光波的起源在观察者的前面而不是后面。如果将这种效应应用于引力波，鉴于光和引力波的传播方式似乎相似，正如 LIGO 和 VIGO 观测所证明的 [26]，一个比光快的观察者将逆序观察引力波，这将使相对于波源的吸引力方向反转。这种效应可能对归因于暗能量的宇宙加速膨胀 [33, 34] 有重要贡献 [27]。

In conclusion, we have introduced the Procrustean Transformations which are based on a refined Doppler effect formulation known as the Procrustean Bed effect. In this theory, light waves undergo changes in their frequency, length and speed. The Procrustean Bed can also provide an explanation for the Ives-Stilwell and Fresnel experiments, and it could be a potential solution for the accelerated expansion of the universe.
总之，我们引入了基于改进的多普勒效应公式（称为普罗克鲁斯特斯床效应）的普罗克鲁斯特斯变换。在这个理论中，光波的频率、波长和速度会发生变化。普罗克鲁斯特斯床还可以为艾夫斯-斯蒂尔韦尔和菲涅耳实验提供解释，并且它可能是宇宙加速膨胀的潜在解决方案。

CRediT authorship contribution statement

CRediT 作者贡献声明

Adolfo Santa Fe Dueñas: Conceptualization, Investigation, Methodology, Writing - original draft, Writing - review & editing.
阿道夫·圣达菲·杜埃尼亚斯：概念化、调查、方法、写作 - 初稿、写作 - 审查和编辑。

Declaration of competing interest

利益冲突声明

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
作者声明他们没有已知的可能影响本文所报告工作的竞争性财务利益或个人关系。

Acknowledgments

致谢

Work at SwRI is supported by NASA, United States grants NX17AI17G, 80NSSC20K1815, and 80NSSC19K0079.
西南研究所的工作得到了美国国家航空航天局的支持，资助号为 NX17AI17G、80NSSC20K1815 和 80NSSC19K0079。

Data availability

数据可用性

No data was used for the research described in the article.
本文所述研究未使用任何数据。

References

1. Maxwell J.C. “On physical lines of force”. London, Edinb, Dublin Philos Mag J Sci, 1861, 21(141), pp. 338–348. DOI: 10.1080/14786431003659180
2. Hunt B.J. The Maxwellians. Cornell University Press, 2005.
3. Weber W., Kohlrausch R. “Ueber die elektricitätsmenge, welche bei galvanischen strömen durch den querschnitt der kette fliesst”. Ann Phys, 1856, 175(9), pp. 10–25. DOI: 10.1007/978-3-663-04516-8˙7
4. Fizeau H. “Sur une expérience relative à la vitesse de propagation de la lumière”. C R, 1849, 29, pp. 90–92. URL
5. Foucault L. “Méthode générale pour mesurer la vitesse de la lumière dans l’air et les milieux transparents. Vitesses relatives de la lumière dans l’air et dans l’eau. Projet d’expérience sur la vitesse de propagation du calorique rayonnant”. CR Hebd Seances Acad Sci, 1850, 30, pp. 551–560. URL
6. Maxwell J.C. “A dynamical theory of the electromagnetic field”. Proc R Soc London, 1864, 13, pp. 531–536. DOI: 10.1098/rstl.1865.0008
7. Einstein A. “Zur elektrodynamik bewegter körper”. Ann Phys, 1905, 322(10), pp. 891–921. DOI: 10.1002/andp.19053221004
8. Poincaré M.H. “Sur la dynamique de l’électron”. Rend. Circ. Mat. Palermo, 1906, 21, pp. 129–175. DOI: 10.1007/BF03013466
9. Lorentz H.A. “Electromagnetic phenomena in a system moving with any velocity smaller than that of light”. In: Collected papers, Springer, 1937, pp. 172–197. DOI: 10.1007/978-94-015-3445-1˙5
   [Google Scholar](https://scholar.google.com/scholar_lookup?title=Electromagnetic phenomena in a system moving with any velocity smaller than that of light&publication_year=1937&author=H.A. Lorentz)
10. Hoffmann B. Relativity and Its Roots. Dover Publications, 2012.
11. Jacobs J.M. “The relativity of light”. 2009.
12. Smarandache F., Yuhua F., Fengjuan Z. “Unsolved problems in special and general relativity”. Infinite Study, 2013. URL
13. Klinaku S. “The “triplet paradox” overthrows the “twin paradox””. Results Phys, 2023, Article 106476. DOI: 10.1016/j.rinp.2023.106476
14. Giuliani G. “Experiment and theory: the case of the Doppler effect for photons”. Eur J Phys, 2013, 34(4), p. 1035. DOI: 10.1088/0143-0807/34/4/1035
15. Ives H.E., Stilwell G.R. “An experimental study of the rate of a moving atomic clock”. J Opt Soc Amer, 1938, 28(7), pp. 215–226. DOI: 10.1364/JOSA.28.000215
    URL
16. Robertson H.P. “Postulate versus observation in the special theory of relativity”. Rev Modern Phys, 1949, 21, pp. 378–382. DOI: 10.1103/RevModPhys.21.378
    URL
17. Grieser R., Klein R., Huber G., et al. “A test of special relativity with stored lithium ions”. Appl Phys B, 1994, 59(2), pp. 127–133. DOI: 10.1007/BF01081163
18. Saathoff G., Karpuk S., Eisenbarth U., et al. “Improved test of time dilation in special relativity”. Phys Rev Lett, 2003, 91, Article 190403. DOI: 10.1103/PhysRevLett.91.190403
    URL
19. Botermann B., Bing D., Geppert C., et al. “Test of time dilation using stored ions as clocks at relativistic speed”. Phys Rev Lett, 2014, 113, Article 120405. DOI: 10.1103/PhysRevLett.113.120405
    URL
20. Cohen M.H., Kellermann K.I., Shaffer D.B., et al. “Radio sources with superluminal velocities”. Nature, 1977, 268(5619), pp. 405–409. DOI: 10.1038/268405a0
21. Chodorowski M.J. “Is space really expanding? A counterexample”. Old New Concepts Phys, 2007, 4(1), pp. 15–33. URL
22. Shapiro A.E. “Huygens’ traité de la lumière and Newton’s opticks: Pursuing and eschewing hypotheses”. Notes Rec R Soc London, 1989, 43(2), pp. 223–247. DOI: 10.1098/rsnr.1989.0016
23. Doppler C. “On the coloured light of the double stars and certain other stars of the heavens. Paper delivered to the royal bohemian society, may 25, 1842”. Abhandlungen Königlich Böhmischen Gesellschaft Wissenschaften, 1843. DOI: 10.1002/andp.18511601007
24. Liang J., Ma C., Zhu L., et al. “Single-shot real-time video recording of a photonic mach cone induced by a scattered light pulse”. Sci Adv, 2017, 3(1), Article e1601814. DOI: 10.1126/sciadv.1601814
25. Wilson R.W. “The cosmic microwave background radiation”. Science, 1979, 205(4409), pp. 866–874. DOI: 10.1126/science.205.4409.866
26. Abbott B.P., Abbott R., Abbott T.D., et al. “GW170817: Observation of gravitational waves from a binary neutron star inspiral”. Phys Rev Lett, 2017, 119, Article 161101. DOI: 10.1103/PhysRevLett.119.161101
    URL
27. Hoh F. “Dark matter creation and anti-gravity acceleration of the expanding universe”. J Mod Phys, 2021, 12(3), pp. 139–160. DOI: 10.4236/jmp.2021.123013
28. Shi X., Lin X., Kaminer I., et al. “Superlight inverse Doppler effect”. Nat Phys, 2018, 14(10), pp. 1001–1005. DOI: 10.1038/s41567-018-0209-6
29. Fizeau M. “On the hypotheses relating to the luminous æther, and an experiment which appears to demonstrate that the motion of bodies alters the velociety with which light propagates itself in their interior”. London, Edinb, Dublin Philos Mag J Sci, 1851, 2(14), pp. 568–573. URL
30. Fresnel A. “Lettre d’augustin fresnel à françois arago sur l’influence du mouvement terrestre dans quelques phénomènes d’optique”. Annales de Chimie et de Physique, 1818, Vol. 9, pp. 57–66. URL
31. Huidobro P.A., Galiffi E., Guenneau S., et al. “Fresnel drag in space–time-modulated metamaterials”. Proc Natl Acad Sci, 2019, 116(50), pp. 24943–24948. DOI: 10.1073/pnas.1915027116
32. Cheung C., Harris D., et al. “Superluminal radio features in the M87 jet and the site of flaring TeV gamma-ray emission”. Astrophys J, 2007, 663(2), p. L65. DOI: 10.1086/520510
33. Hubble E. “A relation between distance and radial velocity among extra-galactic nebulae”. Proc Natl Acad Sci, 1929, 15(3), pp. 168–173. DOI: 10.1073/pnas.15.3.168
34. Freedman W.L., Madore B.F. “The hubble constant”. Annu Rev Astron Astrophys, 2010, 48(1), pp. 673–710. DOI: 10.1146/annurev-astro-082708-101829
    arXiv

---

via：

• The Procrustean Bed effect for light - ScienceDirect
  https://www.sciencedirect.com/science/article/pii/S2211379723009774