论文题目:Filter Pruning via Geometric Median for Deep Convolutional Neural Networks Acceleration
ORAL:CVPR 2019 Open Access Repository
1.软剪枝概念
软剪枝的概念来源于Soft Filter Pruning (SFP)这篇论文,下图阐述了软剪枝(SFP)和硬剪枝(Hard Filter Pruning,HFP)的区别,它们的不同点是HFP在每个epoch后会将卷积核直接剪掉,被剪掉的卷积核在下一个epoch中不会再出现,而SFP在每个epoch后,会将需要剪枝的卷积核仍然保留,只是将其参数置为0,依旧参与下一轮的迭代更新,在所有的epoch循环结束后再进行权重修剪。
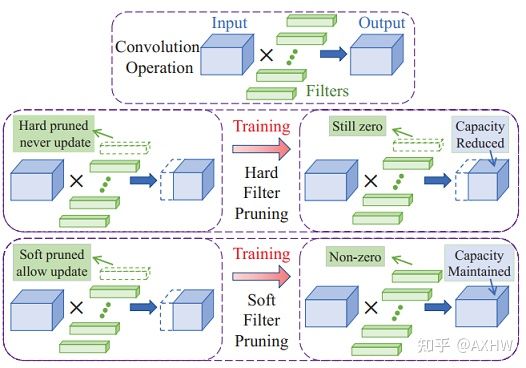
软剪枝与硬剪枝图示
2.SFP与FPGM算法
SFP和FPGM是同一个作者提出的,它们的思路相似,不同之处在于下图中的红色区域,SFP采用的是范数准则,而FPGM采用的是几何中位数准则。SFP算法如左图所示,总体而言包含两个循环结构,第一个循环是epoch,该过程其实就是普通的迭代训练,在每训完一个epoch后开始执行剪枝操作。第二个循环为遍历网络中的每一层,计算每个卷积核的L2-norm(L2范数),并选取L2范数最低的 Ni+1∗Pi 个卷积核进行剪枝,剪枝的表现形式就是将卷积核参数置0。在所有的epoch迭代结束之后,最终得到的模型权重会包含一些值为0的卷积核,将这些卷积核直接去掉就可以得到最终的权重[1]。

2.1FPGM几何距离
算距离的方式如下所示
similar_matrix = distance.cdist(weight_vec_after_norm, weight_vec_after_norm, 'euclidean')假设共有10个卷积核(A1,A2...A10),计算每个卷积核与所有卷积核的距离,如下所示A1的几何距离为:

以此类推得到A2,A3一直到A10的几何距离,然后按照几何距离从小到大排序,将较小几何距离的卷积核置为0。
3.FPGM创新点
提出了一种新的过滤器剪枝方法,即通过几何中值的过滤器剪枝(FPGM)来压缩模型。
与以前的方法(SFP)不同,FPGM 通过修剪带有冗余信息的过滤器而不是那些重要性“相对较低”的过滤器来压缩 CNN 模型。
与之前修剪贡献相对较少的过滤器的方法不同,FPGM 选择具有最大可替换贡献的过滤器。具体来说,我们计算同一层内过滤器的几何中值 (GM) [8]。根据 GM 的特性,它附近的滤波器 F 可以用剩下的滤波器来表示。因此,修剪这些过滤器不会对模型性能产生实质性的负面影响。
4.解决了哪些问题
基于范数的剪枝方法,依赖两个并不总是满足的要求:(1)滤波器的范数偏差应该很大; (2) 滤波器的最小范数应该很小。而 FPGM 不需要这两个要求。
将修剪操作与正常训练过程相结合,因此不需要额外的微调。
5.实验心得
经过训练测试发现:每一层都裁剪掉相同剪枝率的权重,等效于整体的网络宽度直接*剪枝率;比较整体的网络宽度*剪枝率的小网络与每一层都裁剪掉相同剪枝率的权重的裁剪网络是相同的,而且直接训练的整体的网络宽度*剪枝率的小网络的性能不比每一层都裁剪掉相同剪枝率的权重的裁剪网络的性能差,那么fpgm剪枝感觉没起到什么作用啊!
3.关键代码解析
代码逻辑
这里以作者提供的FPGM代码为例,用于ImageNet数据集的图像分类任务,下图展示了各代码之间的逻辑关系,剪枝包含两个步骤,对其进行粗略描述:
第一步:利用imagenet_resnet.py和pruning_train.py训练得到最佳权重Best.pt;
第二步:利用imagenet_resnet_small.py和get_small_model.py对Best.pt进行修剪,将权重置为0的部分剔除得到最终剪枝后的小模型权重Best_pruned.pt。
第三步:在剪枝过后,最后可利用小模型权重进行推理和批量测试。
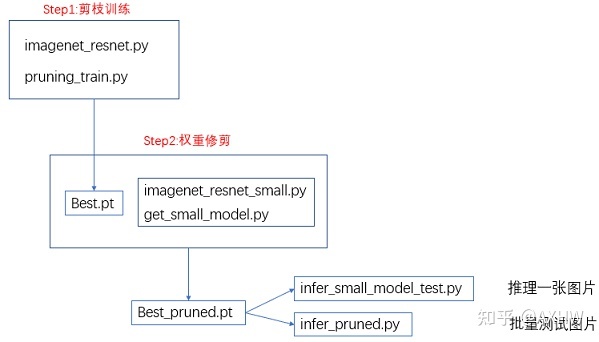
剪枝步骤
参考yolov5软剪枝(二):SFP和FPGM算法解析 - 知乎代码讲解部分,再结合https://github.com/he-y/filter-pruning-geometric-median/blob/76f0ffefbd/pruning_imagenet.py源码进行查看即可,总体比较简单。
参考
yolov5软剪枝(二):SFP和FPGM算法解析 - 知乎
FPGM(Filter Pruning via Geometric Median)笔记_ManiacLook的博客-优快云博客


























 901
901

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








