《机器学习实战3》

2017.3.6
第三章《决策树的构造》

思维导图：

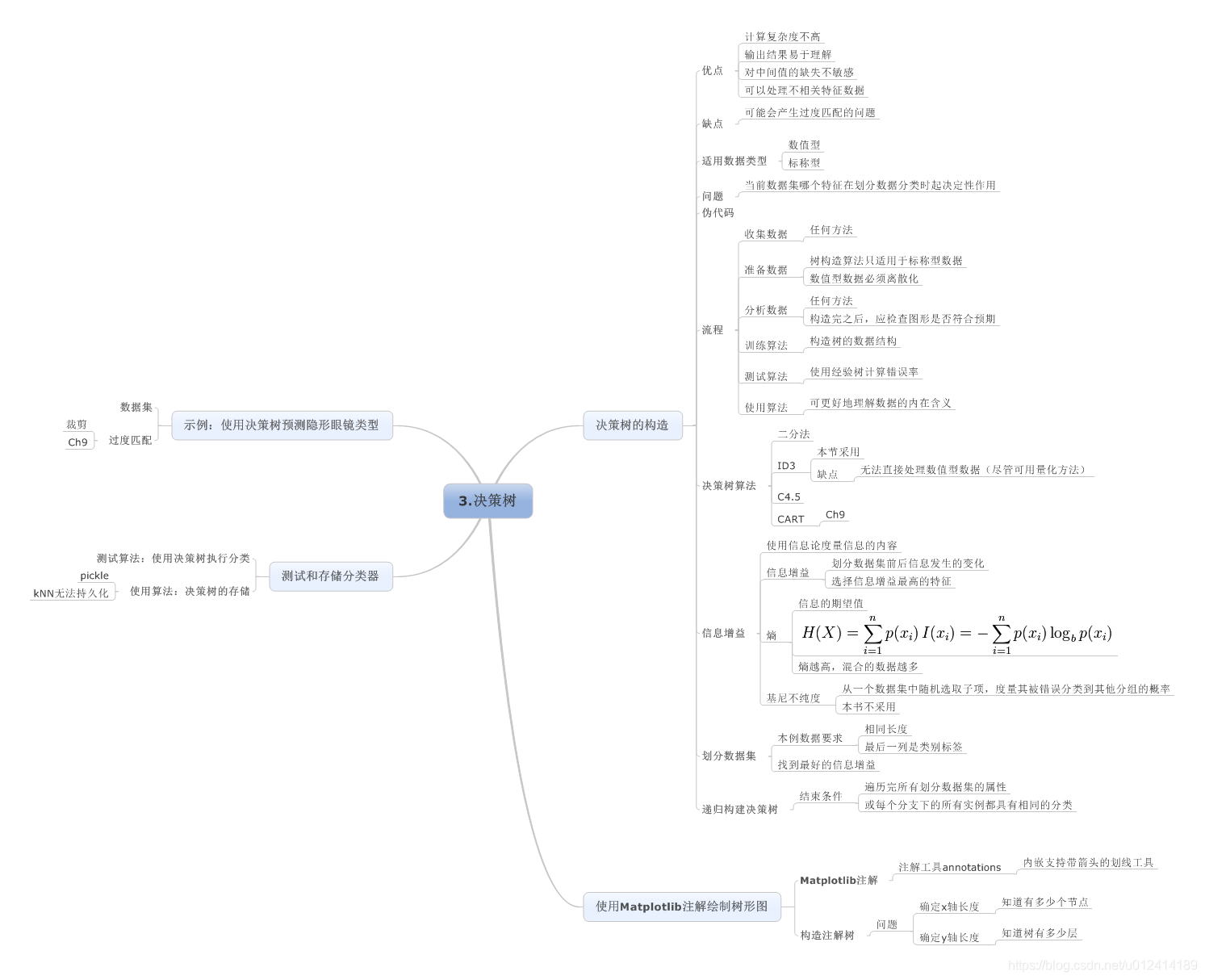
1、基本算法原理

理解数据集中蕴含的知识信息，根据特征进行划分，形成一定的规则，最终形成规则树，按照这个规则树即可以将数据分类出来。
优点：计算复杂度不高，输出结果易于理解，对中间值的缺失不敏感，可以处理不相关特
征数据。
缺点：可能会产生过度匹配问题
适用数据类型：数值型和标称型<>

2、构造一颗决策树的流程：

检测数据集中每一个子项的属性是否属于同一类

     if so return 类标签；
     else
         寻找划分数据集的最好特征
         划分数据集
         创建分支结点
            for 每个划分的子集
                调用createBranch并增加返回结果到分支结点中
         return 分支结点

3、决策树的一般流程：

(1)收集数据：可以使用任何方法。
(2)准备数据：决策树算法只适用于标称型数据，数值数据必须离散化
(3)分析数据：树构造完成之后检查是否符合预期
(4)训练算法：构造树的数据结构
(5)测试算法：计算错误率

---

1、信息增益

划分数据集前后信息发生的变化就是增益，活动的信息增益最高的特征就是最好的选择。换句话说，信息增益以及“熵”(entropy)就是决策树的属性选择函数。熵就是数据集中信息的无序性的体现，这和其他领域中熵的意义是一样的。
书里用到的熵的计算方法如下：

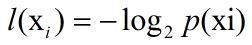
其中p(xi)是选择分类的概率
还有所有类别的信息期望值：

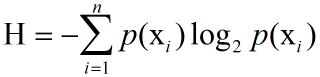
完成上述计算熵的代码如下：

def calcShannonEnt(dataSet):
    numEntries = len(dataSet)
    labelCounts = {
   
   }
    for featVec in dataSet: #the the number of unique elements and their occurance
        currentLabel = featVec[-1]
        if currentLabel not in labelCounts.keys(): labelCounts[currentLabel] = 0
        labelCounts[currentLabel] += 1
    shannonEnt = 0.0
    for key in labelCounts:
        prob = float(labelCounts[key])/numEntries
        shannonEnt -= prob * log(prob,2) #log base 2
    return shannonEnt

2、划分数据集

划分数据集的关键在于寻找恰当的特征值来进行划分。我们需要尝试数据集中的每一个特征值的划分并且计算该划分的熵。通过比较得出最终的结果。
根据给定特征值划分数据集：

def splitDataSet(dataSet, axis, value):
    retDataSet = []
    for featVec in dataSet:
        if featVec[axis] == value:
            #把特征值去除
            reducedFeatVec = featVec[:axis]     
            reducedFeatVec.extend(featVec[axis+1:])
            retDataSet.append(reducedFeatVec)
    return retDataSet

依次计算数据集中去除某一特征值余下集合的熵，取得熵增最大值的特征值，就是划分数据集的特征值。

def chooseBestFeatureToSplit(dataSet):
    numFeatures = len(dataSet[0]) - 1      #the last column is used for the labels
    baseEntropy = calcShannonEnt(dataSet)
    bestInfoGain = 0.0; bestFeature = -1
    for i in range(numFeatures):        #iterate over all the features
        featList = [example[i] for example in dataSet]#create a list of all the examples of this feature
        uniqueVals = set(featList)       #get a set of unique values
        newEntropy = 0.0
        for value in uniqueVals:
            subDataSet = splitDataSet(dataSet, i